多服务窗等待制M/M/n排队模型

付馨雨，罗国旺

(重庆师范大学数学学院，重庆 400047)

在日常生活中，经常可以看到许多排队模型同时具有可变输入率与可变服务率的特性，如银行储蓄排队、大型超市付款台排队等均属此类排队模型。即当服务窗口前排队顾客较多时，顾客会犹豫是否加入系统排队等待;而服务人员为了避免损失顾客，就会适当地提高服务速度。关于具有不耐烦顾客的排队模型已有很多学者进行了研究，文献［1－5］研究了具有不耐烦顾客的M/M/1及M/M/n排队模型。然而，有关将可变输入率和可变服务率与具有不耐烦顾客相结合的M/M/n排队模型还未得到学者关注。本文研究了输入率可变且具有两类服务率及不耐烦顾客的M/M/n排队模型。

1 模型假设

为了方便对多服务窗等待制M/M/n排队模型的研究，做如下假设:

1)系统中有n个服务窗口，容量无限。

2)顾客到达系统的时间间隔服从参数为λ的指数分布。

3)假定顾客到达系统后加入队列的概率为αk(0＜αk＜1)，即 αk依赖于队长 k。当 k→∞时，αk→0，此时的输入率 λk=αkλ。在此仅讨论

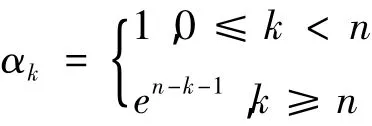
4)多个服务台间相互独立，当系统中排队长度超过n时，服务窗用快速服务率μ2，反之则用慢速服务率μ1。

5)服务时间与顾客到达的时间相互独立，且系统中的顾客排成一个队。

6)记βk为具有不耐烦顾客离开的概率，k表示等待队长(此时系统中已有n+k个顾客)。队伍中不耐烦顾客离开队伍的强度δ≥0。

2 数学模型

根据上面的假设不难得到以下定理:

定理1 令X(t)表示时刻t系统中的顾客数(队长)，则{X(t)，t≥0}是以状态空间为 E={0，1，2，3，…}且

的生灭过程。

证明 略，可参见文献［3－4］。

画出系统状态流图，见图1。

图1 多服务窗等待制M/M/n模型的状态流图

3 平稳分布

由以上的数学模型得到模型的平稳分布，即定理2。

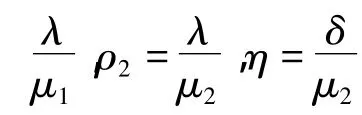
证明 由图1可列出平衡条件下的k氏代数方程，并求出其平稳分布，解析表达式为:

4 主要指标

根据平稳分布，得到如下主要数学指标。

1)顾客排队等待的概率。由式(2)可得顾客排队等待的概率为

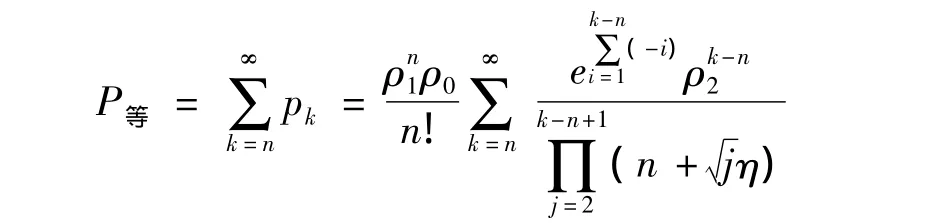
2)平均等待队长(系统内排队等待顾客数的均值)。首先等待队长lq有如下分布列:

3)平均繁忙中的服务窗个数。注意到繁忙中的服务窗个数Y有如下分布列:

4)系统的平均队长(系统内顾客数的均值)为

5)单位时间内平均离开队列的不耐烦顾客数为

6)绝对通过能力(单位时间内被服务完的顾客均值)为

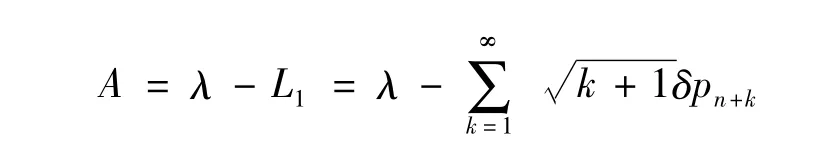
7)相对通过能力为

8)由little公式得顾客在系统中的平均逗留时间和平均等待时间:

5 结束语

本文研究了可变输入率且具有两类服务率及不耐烦顾客的M/M/n排队模型，充分考虑了输入率、服务率以及不耐烦顾客与系统中队长的关系，并获得了该模型的平稳分布和主要指标。该模型可以帮助解决银行、超市、商场等服务行业中的不同输入率、不同服务率以及不耐烦顾客问题，从而将文献［2］推广到更为一般的情形，使其更具有普遍性，为实际运用提供了一定的理论基础。

［1］陆传赉.排队轮［M］.北京:北京邮电大学出版社，2009.

［2］李焕.具有可变输入率和不耐烦顾客M/M/n的排队模型［J］.重庆师范大学学报:自然科学版，2011(3):49 －52..

［3］孙荣恒，李建平.排队论基础［M］.北京:科学出版社，2002.

［4］孙荣恒.随机过程及其应用［M］.北京:清华大学出版社，2004.

［5］台文志，高世泽.一类具有可变输入率的M/M/1排队模型［J］.重庆师范大学学报:自然科学版，2009，26(1):69－72.

［6］刘次华.随机过程及其应用［M］.北京:高等教育出版社，2004.

［7］唐应辉，唐小我.排队论基础与分析技术［M］.北京:科学出版社，2006.