融合时间戳和同态签名的安全网络编码方法

裴恒利，尚涛，刘建伟

（北京航空航天大学 电子信息工程学院，北京 100191）

1 引言

网络编码技术[1]因有利于无线多跳网络传输性能的提升而成为近年的研究热点，但同时它也带来了许多安全问题。例如，在无线多跳网络中，网络编码特别容易受到恶意节点的污染攻击[2]，同时也会遭受传统网络中存在的重放攻击、假冒攻击、篡改攻击、拒绝服务攻击、中间人攻击等[3]。针对污染攻击，Ho等利用简单多项式散列函数（simple polynomial hash function）在目的节点处对消息的完整性进行验证[4]，然而，中继节点并未参与完整性验证，因此相应地会增加受攻击的数据分组在网络中的传输数量。Gkantsidis和Rodriguez提出的同态散列方案(homomorphic hashing scheme)[5]实现了中继节点对消息完整性的验证，但却需要额外的安全信道来传输原始消息的散列值。随后，Charles等在同态散列方案的基础上设计了一种同态签名方案(homomorphic signature scheme)[6]，该方案不需要额外的安全信道，但由于复杂的韦伊配对操作（weil pairing operation）会增加运算的复杂度，因此，其应用受到了限制，而Yu等提出的基于RSA的同态签名方案[7]则大大降低了同态签名的运算复杂度。Rosario等[8]对Yu的方案进行了改进，将基于RSA的同态签名方案设计在整数域中，并通过随机预言模型（random oracle model）证明了该方案的安全性。

虽然同态签名方案能够抵御污染攻击，但由于网络中攻击形式的多样性，设计可同时抵御包含污染攻击在内的多种攻击网络编码签名方案非常重要。尤其是对能量受限的无线传感器网络而言，节点的能量是制约网络性能提升的主要因素，而重放攻击因会大量消耗节点能量而成为此类网络所面临的最棘手的攻击之一。因此，针对能量受限的无线多跳网络，本文在基于RSA同态签名方案的基础上设计了一种融合时间戳和同态签名的可同时抵御污染攻击与重放攻击的网络编码签名方案——该方案将对时间戳和对数据的签名有效地结合起来，保证了网络中各节点可以同时认证数据的完整性和时间戳的真实性；并进一步分析了引入时间戳对网络编码解码概率的影响以及对网络开销的影响。

2 相关研究

2.1 随机线性网络编码

网络编码按照编码系数产生方式的不同可分为随机性网络编码和确定性网络编码，按照编码方式的不同可分为线性网络编码和非线性网络编码[9]。根据无线多跳网络的分布式特点，以下重点介绍随机线性网络编码的具体过程。

网络拓扑如图1所示。其中，A为源节点，(t1,…,tk)为目的节点，其他各节点为中继节点。源节点将要发送的每一条原始消息设定为选自有限域Zq的长度为n的向量，其中，q是预先定义的素数。因此，原始消息Mi可表示为

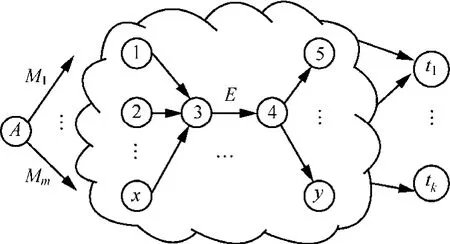
图1 网络拓扑

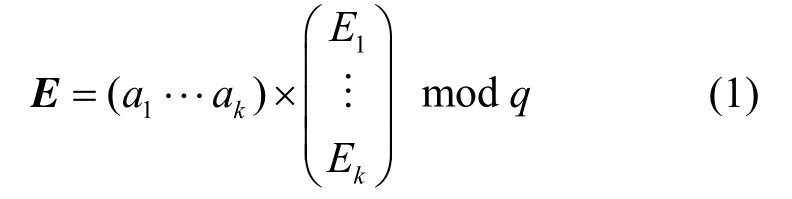
在随机线性网络编码中，每一个中继节点将收到的消息线性组合，生成编码消息E并转发。因此，E可表示为该中继节点所收到的消息的线性叠加，即

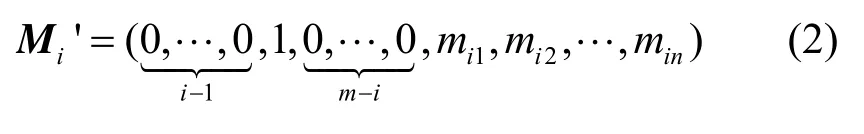
相应地，中继节点收到的消息向量E’记为

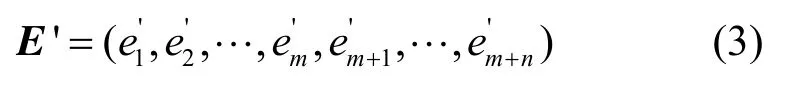
其中，Mi’、E’可统称为扩展消息或扩展向量（augmented message）[10]。为防止攻击者截获从源节点发出的原始消息，源节点对其所要发送的消息也要进行编码，即对要发送的 m条扩展消息进行m次线性组合，获得m条编码消息并转发。

目的节点在收到m条线性无关的消息(E1’, …,Em’)后，即可得矩阵 ′U为

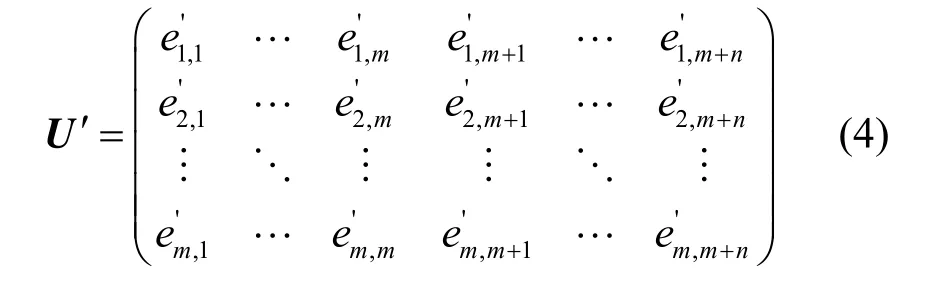
将矩阵 U ′的前 m列构成的矩阵记作 U，后 n列构成的矩阵记作V，则由式(5)便可将源节点发送的m条原始消息解码恢复。

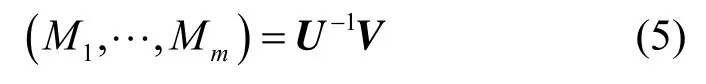
2.2 同态签名

同态分为加法同态和乘法同态[11]。给定变量X1和X2，若对于函数Φ，存在函数f使得式(6)成立，则称函数Φ满足加法同态。

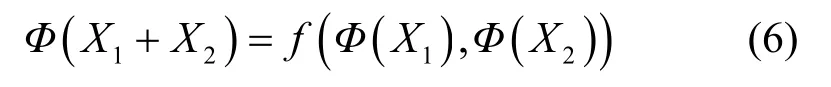
若对函数Φ，存在函数f使得式(7)成立，则称函数Φ满足乘法同态。

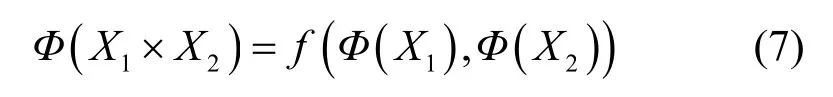
同态签名便是利用了同态函数保持运算的性质。节点接收的消息与相应签名分别记作和若当前节点要对接收到消息的线性组合生成签名S，如果Φ具有加法同态性，则当前节点可直接由式(8)生成签名。其中，由式(8)计算出的签名S与相等，这样便实现了中继节点在未知源节点私钥的情况下对所要发送的消息进行签名。本文安全网络编码方案中的签名函数具有加法同态性，详见第 3节中命题1的证明。

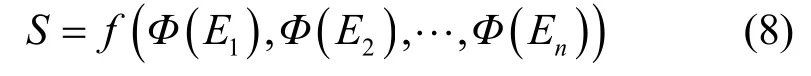
3 安全网络编码方案

在安全网络编码方案中，时间戳信息可以起到两方面作用：一是网络中各节点可以利用时间戳来识别重放消息，以抵御网络中的重放攻击；二是以时间戳为源产生网络编码的随机系数，可以保证网络中各节点能够利用签名函数的加法同态性对编码后的消息产生签名。因此，本文在利用基于RSA同态签名方案抵御污染攻击的基础上，引入时间戳设计新型同态签名方案以抵御网络中的重放攻击，并以时间戳为源生成网络编码的随机系数。

网络拓扑如图1所示。A为源节点，不规则区域内的节点为中继节点，为目的节点，表示由原始消息生成的扩展消息，由长度为m + n 的向量表示。全网采用同步时钟，且所有中继节点均对收到的消息编码。方案中的相关参数如表1所示。

方案仍采用传统的基于RSA的同态签名方案，但由于在签名方案中引入了时间戳机制，为保证签名仍具有同态属性，方案考虑以时间戳为源生成网络编码的随机系数，具体过程如下。

Step1 源节点选取参数。与基于RSA的同态签名方案相类似，参数选取过程简述如下。

表1 相关参数

Step2 源节点生成签名。在源节点的签名生成过程中引入了时间戳，对消息和时间戳的组合生成签名。

源节点产生 m条扩展消息并附上当前时刻作为该条消息的时间戳（需将时间戳 Ti转换为 Zq中的数值），然后用私钥d对m条消息签名，其中，签名 SIGNd(Mi’||Ti)如式(9)所示。

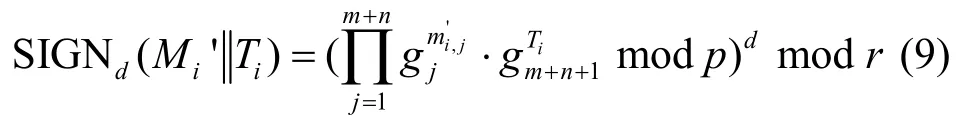
Step3 中继节点验证签名并生成新的签名。具体过程如下。

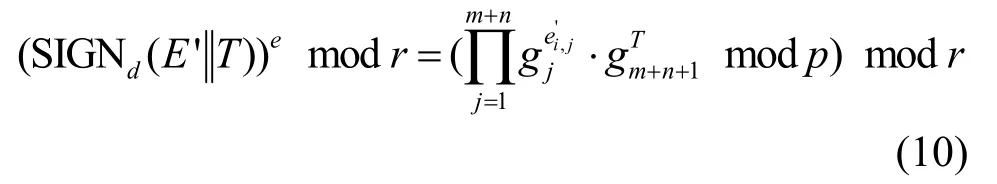
如果式(10)成立，则可断定该消息组合没有受到污染攻击，这是因为：若该消息组合在传输过程中的数据部分没有遭到破坏，则式(11)成立。

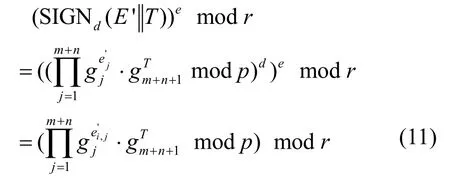
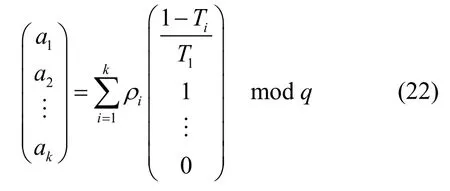
然后由消息组合中的时间戳部分判断该消息组合是否被重放，如果为重放消息则丢弃。若消息组合在时效范围内，则该节点在收到k条消息组合k)后，为保证能够利用同态性质对此k条消息组合中数据部分的线性组合进行签名，则需根据当前时刻T以及收到的k条消息组合中的时间戳由式(12)计算出随机系数

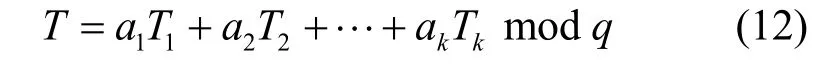
利用该组随机系数对收到的k条消息组合中的数据进行线性叠加，得到编码数据 E’||T：即，并利用签名的同态性质，由k条消息组合中的签名生成与E’||T对应的签名 SIGNd(E’||T)。

命题1函数SIGNd具有加法同态性。

证明设是长度为m+n+1的向量，则由式(9)可得

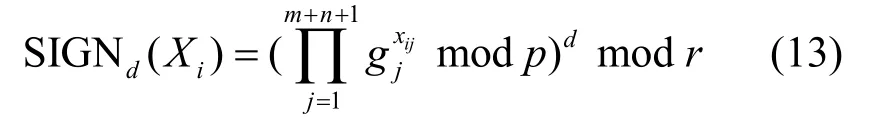
因此

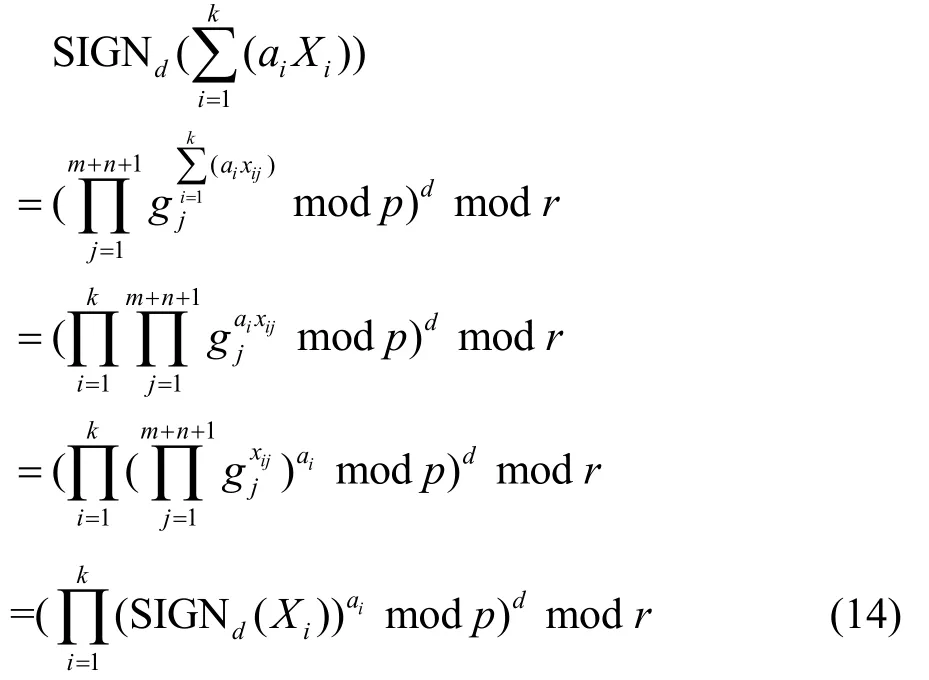
命题得证。

因此可利用同态性质生成对消息 E’||T的签名SIGNd(E’||T)，式(15)给出了该签名的计算式。

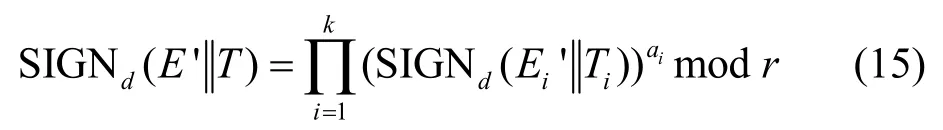
然后，节点将消息组合{E’||T, SIGNd(E’||T)}转发。

Step4目的节点验证签名并对源节点发送消息解码恢复，具体过程如下。

目的节点在收到一条消息组合后，首先通过式(10)来判断消息是否受到污染攻击，然后等待。当接收到 m条线性无关的消息组合后，利用式(5)对源节点发送的消息解码恢复。

4 安全性分析

本文的安全网络编码方案中假设源节点总是安全的，只有中继节点不可信。攻击者可能会控制中继节点，破坏其所要发送的消息，对网络实施污染攻击；另外，攻击者也可能会控制中继节点，使其重复发送已经发送过的消息，对网络实施重放攻击。

4.1 污染攻击的安全性分析

攻击者的污染攻击方式分为2种：一是产生伪造消息数据并对其生成有效签名；二是根据攻击者所截获的消息组合中的签名产生与之相匹配的消息数据。

在第一种攻击方式中，攻击者污染中继节点接收到消息组合中的数据部分或直接将伪造的消息数据注入网络，中继节点编码后的消息因此遭到污染。将攻击者污染后的消息记作，则中继节点编码后的消息与未受攻击时所产生的编码消息E'T不同，即

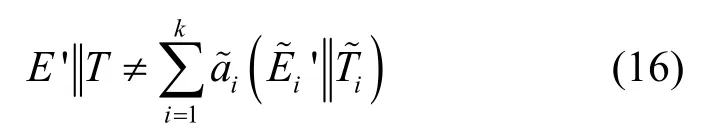
但由于攻击者未知源节点私钥，因此无法对该污染消息生成有效签名，所以攻击无效。

在第二种攻击方式中，攻击者依照截获的消息组合中的签名生成与之匹配的数据，即希望根据所截获的消息组合中的签名推出与之相应的数据因此，该方案的安全性等同于是否可以找到不同于E'T的数据E˜'T˜，使得，下面将证明其困难度等价于解决离散对数问题。

命题2给定消息E'T和相应签名找到不同于E'T的消息E˜'T˜，使得的困难度等价于解决离散对数问题。

证明为简化说明，考虑 m = n =1的特殊情况，此时，

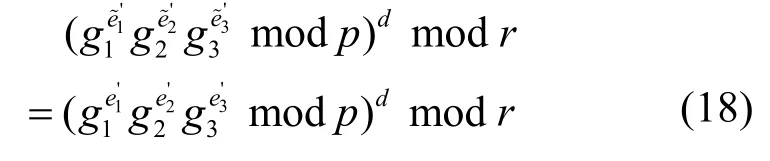
固定 e˜ 1'和 e˜2'，令 x = e˜3'，式(18)变换为

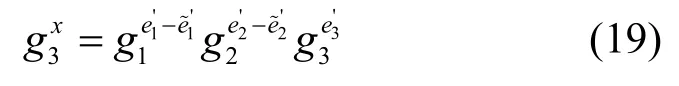
则问题转化为希望找到 x使其满足式(19)。可以看出由式(19)求解x是一个离散对数困难问题，命题2得证。

4.2 重放攻击的安全性分析

在重放攻击中，攻击者截获网络中的消息组合并不断转发或通过控制中继节点使其重复发送已发送过的消息组合，从而达到消耗网络节点能量、占用网络带宽和降低网络吞吐量等目的。

在该攻击中，攻击者有2种攻击方式：直接重放所截获的消息组合或修改所截获消息组合中的时间戳并对其生成有效签名。

第二种攻击方式相当于污染攻击中的第一种攻击方式：对伪造数据生成有效签名。攻击者由于未知源节点的私钥，因此无法对截获的消息组合中的数据部分进行签名，所以攻击无效。

由以上安全性分析可知，本文提出的安全网络编码方案可同时抵御污染攻击和重放攻击，且攻击成功的困难度等同于解决离散对数困难问题。

5 性能分析

5.1 开销分析

为了分析安全网络编码的性能，本节重点考虑签名算法所引发的开销，不考虑引入同步计时机制带来的开销。网络中传送的消息组合以{E ' T ,的形式出现，其中，E'T为数据，以向量形式表示，为签名。由于时间戳T的引入使网络开销相较于基于RSA的同态签名方案有所增加，现将增加的开销类型分类如下（下文中为叙述简便，称基于 RSA的同态签名方案为方案 1，本文的引入时间戳的同态签名方案为方案2，且开销均指算法耗费时间）。

1) 参数初始化开销

参数初始化阶段耗费时间近似正比于方案所需 gi的个数，与方案1相比两者的耗费时间比值近似等于，且m和n数值越大该比值越接近于1。

2) 编解码与求解线性方程组的开销

3) 计算签名的开销

网络中有2类节点产生签名：源节点和中继节点。由于源节点仅有1个，而中继节点数目较多，因此签名开销主要产生在中继节点。其中，中继节点生成签名的运算如式(9)所示，将方案 1中的签名记作SIGNd(E ') ，方案2中的签名记作，由于两者均取值于有限域 Zr中，且随机系数均选自有限域Zq，因此，对两者作k次模指数运算的开销比值近似接近于1。

4) 验证签名的开销

中继节点的主要功能是对收到的签名进行验证。验证过程应保证尽可能地快速。然而，由于签名采用基于 RSA的公钥签名体制，使得签名的验证时间成为了制约网络性能提升的主要因素。因此，衡量方案性能的最重要指标是签名算法的验证时间。

模指数运算是算法效率的制约因素。由式(10)可知，方案2的签名验证过程（验证一条消息）需经过次模指数运算，而方案1的签名验证过程仅需运算次，因此两者的签名验证时间的比值为，且m与n的值越大，该比值越接近于1。

由以上分析可知，与方案1相比，方案2仅在参数初始化与签名验证部分增加了网络的开销，而签名、编解码与求解线性方程所引起的网络开销与方案1基本一致。

5.2 网络编码解码概率分析

随机线性网络编码中随机系数的生成和选取对目的节点的解码概率有一定影响，而本文网络编码方案中的随机系数通过求解 k元一次方程组产生，与传统的随机系数的产生方式有所不同，究竟对解码概率有多大影响，需要进一步详细分析。

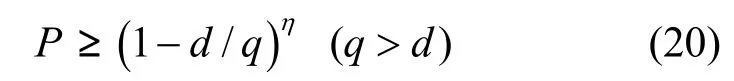
其中，d表示网络中目的节点的个数，q为有限域的大小，η为源节点所发消息的个数。

证明 在随机线性网络编码网络中，若随机系数满足 Zq中的均匀分布且相互独立，则目的节点解码概率P的取值范围为因此，命题3可转化为证明式(12)的k个解满足独立均匀分布。

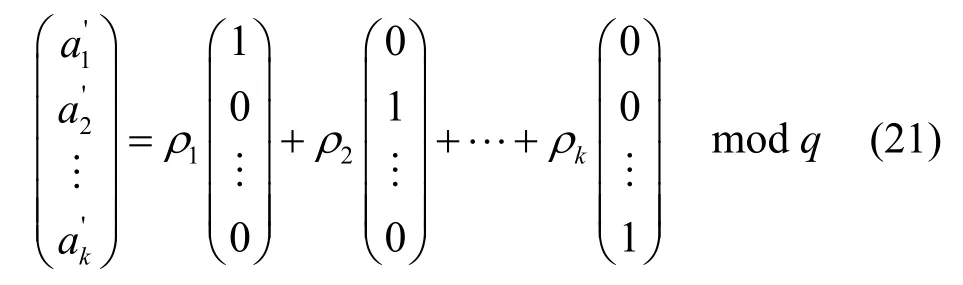
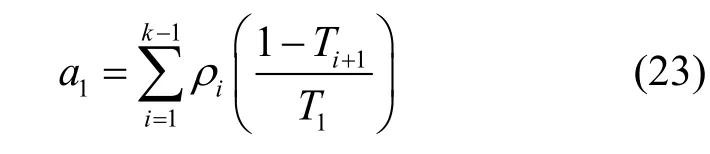
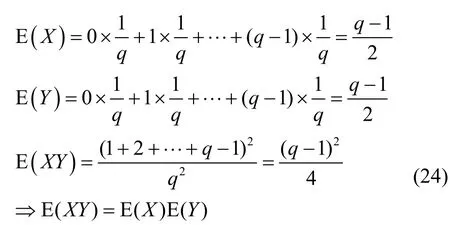
由上述分析可得a1满足均匀分布且与(a2,…,ak)相互独立，命题3得证。

6 仿真分析

6.1 时耗分析

利用 NS2网络仿真软件对本文所介绍的安全网络编码方案进行仿真。其中，传输层采用UDP数据流，网络层协议采用洪泛协议，编码尺寸设定为2，网络拓扑如图2所示。A表示源节点，D表示目的节点，1、2、3、4、5节点表示中继节点。

图2 网络拓扑

改变源节点消息向量中元素的个数m，将基于RSA的同态签名方案记为RSA方案，所得的算法运行时间对比如图3所示。

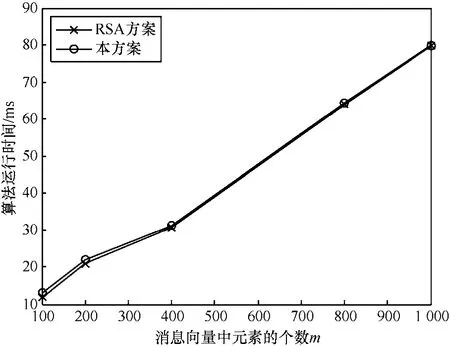
图3 本方案和RSA方案的运行时间对比

从图3中可以看出，随着消息向量中元素个数的增加，2方案的算法运行时间基本呈线性增长。另外，随着m的增大，2方案的曲线基本重合，这是因为算法中引入的时间戳T可以看作消息向量m中的一个元素，随着m值的增大，引入时间戳带来的时耗在整个算法时耗中所占的比重越小。

由上述分析可知，同5.1节中的理论分析结果相一致，本方案和RSA方案的算法时耗基本一致，并且由于本方案能够同时抵御污染攻击和重放攻击，因此综合考虑算法时耗与安全性能，本方案优于RSA方案。

6.2 能耗分析

本小节分析了当网络遭遇重放攻击时，本方案、RSA方案以及未引入安全机制的网络编码方案（简记为编码方案）的节点能耗。

网络中节点所处理的数据分组类型分为2种：重放数据分组和非重放数据分组。

对于重放数据分组，3种方案中节点的处理过程可分为以下3点。

1) 本方案。判断其是否为重放分组（表2中简记为判断），如果为重放分组，则将其丢弃。

2) RSA方案。验证签名、编码、计算签名（表2中简记为验证编码签名）。

3) 编码方案。编码。

对于非重放数据分组，3种方案中节点的处理过程可分为以下3点。

1) 本方案。验证签名、编码、计算签名。

2) RSA方案。验证签名、编码、计算签名。

3) 编码方案。编码。

利用 MATLAB计算上述不同处理过程的运行时间，当消息向量中元素个数m=256时，得到处理过程的运行时间如表2所示。

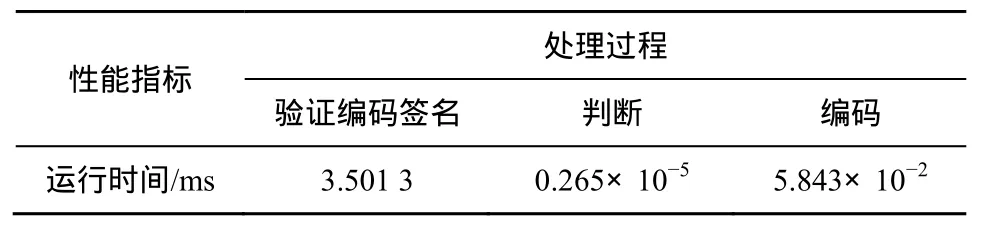
表2 不同处理过程的运行时间

利用公式 W ( 能 量) = P ( 功 率) × T (时 间) 可计算出每种处理过程对应的能耗。固定网络中非重放数据分组的个数为10，改变重放数据分组的个数，结合表2中的数据，可得3种方案中节点的能耗对比如图4所示。

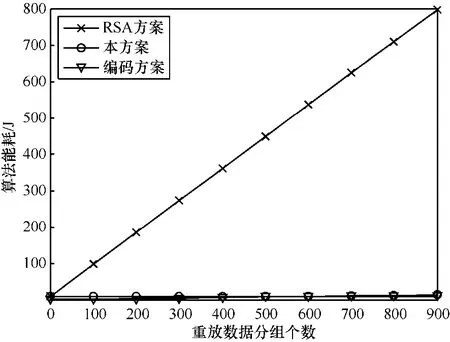
图4 本方案、RSA方案以及编码方案的能耗对比

从图4中可知，RSA方案的能耗远远高于其他2种方案，因此，在网络遭遇重放攻击时，相较于仅可抵御污染攻击的 RSA方案，本方案能够很好地节省节点能量，延长节点的生存时间。

图5为排除RSA方案后，本方案与编码方案的算法能耗对比。

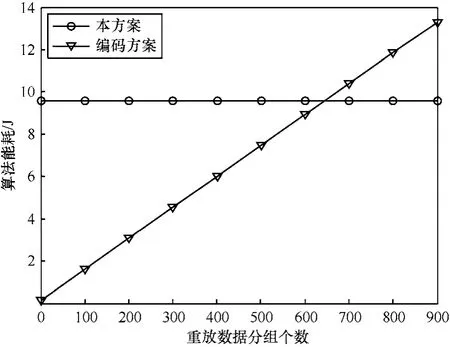
图5 本方案和编码方案的能耗对比

由图5可知，当重放数据分组的个数较小时，相较本方案，编码方案的能耗较小；随着重放数据分组个数的增加，编码方案能耗呈线性增长，而本方案的能耗基本不变。

由上述分析可知，相较于未引入安全机制的网络编码方案，本方案更能够抵御恶意节点重放攻击所带来的能耗，可以更好地延长节点的生存时间。

7 结束语

本文的安全网络编码方案利用融合时间戳的同态签名来抵御网络中的污染攻击和重放攻击，为保证中继节点能够利用同态性质对编码后的消息生成新的签名，需要以时间戳为源来生成网络编码的随机系数。文中重点分析了本方案产生随机系数的方式对网络编码解码概率的影响，并建立攻击模型证明方案可同时抵御污染攻击和重放攻击，性能分析表明该方案与基于 RSA的同态签名方案开销比值接近于 1，因此，网络中各节点并不会因为增加了对时间戳的处理步骤而增长数据处理时间。

[1] AHLSWEDE R, CAI N, LI S. Network information flow[J]. IEEE Transactions on Information Flow, 2000, 46(4)∶1204-1216.

[2] 曹张华, 唐元生. 安全网络编码综述[J]. 计算机应用, 2010, 30(2)∶499-505.CAO Z H, TANG Y S. Survey on secure network coding[J]. Journal of Computer Application, 2010, 30(2)∶499-505.

[3] PERVAIZ M, CARDEI M, WU J. Routing security in ad hoc wireless networks[J]. Network Security, 2010, 117-142.

[4] HO T, LEONG B, KOETTER R. Byzantine modification detection in multicast networks using randomized network coding[A]. Proceedings of IEEE International Symposium on Information Theory(ISIT)[C].Massachusetts, USA, 2008. 2798-2803.

[5] GKANTSIDIS C, RODRIGUEZ P. Cooperative security for network coding file distribution[A]. Proceedings of International Conference on Computer Communications(INFOCOM)[C]. Barcelona, Spain, 2006.367-380.

[6] MENEZES A, OKAMOTO T, VANSTONE S. Reducing elliptic curve logorithms to logorithms in a finite field[J]. IEEE Transactions on Information Theory, 1993, 39(5)∶1639-1646.

[7] YU Z, WEI Y, RAMKUMAR B. An efficient signature-based scheme for securing network coding against pollution attacks[A]. Proceedings of International Conference on Computer Communications (INFOCOM)[C].Arizona, USA, 2008. 1409-1417.

[8] GENNARO R, KATZ J, KRAWCZYK H. Secure network coding over the integers[J]. Public Key Cryptography, 2010, 60(56)∶142-160.

[9] LIM S H, KIM Y H. Noisy network coding[J]. IEEE Transactions on Information Theory, 2011, 57(5)∶3132-3152.

[10] LIM S H, GERLA M, KRAWCZYK H. Performance evaluation of secure network coding using homomorphic signature[A]. Proceedings of International Symposium on Network Coding(NetCod)[C]. Beijing,China, 2011. 1-6.

[11] SUTAR S G, PATIL G A. Privacy management in cloud by making use of homomorphic functions[J]. International Journal of Computer Applications, 2012, 37(2)∶13-16.

[12] CAI N, SHI X, MEDARD M. Localized dimension growth in random network coding∶ a convolutional approach[A]. Proceedings of IEEE International Symposium on Information Theory(ISIT)[C]. St Petersburg, USA, 2011. 1156-1160.

[13] 刘凤梅, 李世取, 黄晓英. 取值于有限域上的独立随机变量和的极限分布定理[J]. 河北工业大学学报, 1999, 1(28)∶98-102.LIU F M, LI S Q, HUANG X Y. Limit distribution theorem for a sum of independent random variables whose values belong to a finite field[J].Journal of Hebei University of Technology, 1999, 1(28)∶98-102.