基于拍卖的P2P内容分发网络带宽分配机制

张云鹤，朱艳琴，纪其进

(1. 苏州大学 计算机科学与技术学院，江苏 苏州 215006；2. 江苏省计算机信息处理技术重点实验室，江苏 苏州 215006)

1 引言

P2P内容分发网络中的节点可以自由地提供或者获取服务，没有中心控制节点约束它们的行为，因此可能存在大量的自私节点。当这些节点面对这样一种处境，即将自己有限的资源用于服务自己，还是无私地奉献给其他节点，以期待将来其他节点也会无私的帮助自己时，通常会选择将有限的资源保留给自己使用。此外，由于获取服务时无需付出任何代价，自私节点会无节制地使用整个系统中紧缺的带宽资源。这使得P2P网络中存在较为严重的搭便车（free-riding[1]）现象，甚至最后出现“公共地悲剧”[2]。当前，针对这一类问题的基本解决方案是引入各种虚拟货币机制，但这些机制均需中心控制节点，有违P2P网络最初的构想目标。

随着应用P2P技术共享节点资源的日渐盛行，越来越多的研究者致力于P2P系统资源交易激励机制的研究。文献[3]中的作者给出基于VCG机制的网络资源分配机制，虽然能够解决自私用户抢占网络资源，但是该机制假设资源管理者存储着所有用户的效用函数，形成了中心节点瓶颈，故会严重影响P2P网络的扩展性；文献[4]提出了一种基于节点历史贡献值的差分服务机制，但由于依据的是历史贡献值，故无法遏制当前节点的自私行为；BitTorrent[5]使用“tit-for-tat”机制激励节点为其他节点服务，能够减少搭便车现象的发生，但是并没有考虑接入带宽的异质性，使得接入带宽较小的节点失去公平竞争的机会。

本文借用经济学中的拍卖方法设计合理的带宽分配机制，使得P2P节点的带宽分配依赖于其“带宽支付”能力，迫使获取服务的节点主动贡献相应的带宽，用于服务潜在的资源请求节点。本文中的机制将无需增加额外的中心服务器，它将请求节点所获得的带宽资源与该节点愿意贡献的带宽资源相关联，能够有效避免“公共地悲剧”的发生，并且不影响新节点公平竞争资源，从而可以使得整个P2P系统中的节点良性竞争使用带宽资源。

2 P2P带宽分配的基本拍卖模型

2.1 系统模型

在本文中考虑由N个节点组成的网状结构P2P内容分发网络。节点间定期交换资源请求以及进行资源分配，假设在资源分配期间网络是稳定的，即不考虑节点的加入或者退出。对于节点的动态加入和离开的情况，本文应用周期性的更新系统信息和节点数量的方法处理。在本文研究中，资源节点只考虑其他节点对于自己拥有的内容数据的请求信息。由于数据传输的主要资源是带宽，因而可以把资源请求抽象成带宽请求。由于P2P网络中请求节点和资源节点的对称性，本文以某个资源节点为主要建模对象。

每个节点接入骨干网时拥有接入带宽为Cibit/s，且上载带宽和下载带宽共享该接入带宽。假设骨干网拥有足够高的带宽容量，则无需考虑骨干网中的路由及时延问题。整个P2P系统的性能瓶颈集中在接入带宽上，实质问题是上载和下载带宽的比例如何设置。由于节点的自私性，传统机制下节点通常会设置较低的上载带宽比例，甚至为零，这使得整个系统中可为其他节点服务的上载带宽资源极其稀缺。

拍卖问题的原型是将N个物品通过竞拍分配给M个购买者，其中，M＞N，以达到最大化社会效益或者最大化拍卖者利益的目标。20世纪末开始，一些研究者将拍卖机制从微观经济学引入到网络资源的分配中[6～9]。故对于上述 P2P网络中的某个资源节点，可以将其拥有的可提供给其他节点的上载带宽视为可分割的拍卖物品，向该资源节点发出资源请求的节点视为购买者，则带宽分配问题可以采用拍卖模型来建模。为了遏制节点的搭便车行为，成功拍得所需带宽的请求节点需要以上载带宽作为支付。

定义 1 节点拥有的空闲的、未分配的上载带宽称为可拍卖带宽，也称可提供服务带宽。

定义 2 用于表示节点对于所分配到的上载带宽满意程度的函数称为效用函数，该函数具有如下性质：连续性、递增性、严格凹的和可微性。

假设资源节点拥有可拍卖带宽为 Ws，请求节点有N个，节点的私有效用函数为 Ui(⋅)，xi是资源节点依据竞价 bi分配给请求节点i的带宽数，则为带宽分配向量。在该模型下，系统最优化问题就是求解式（1）。

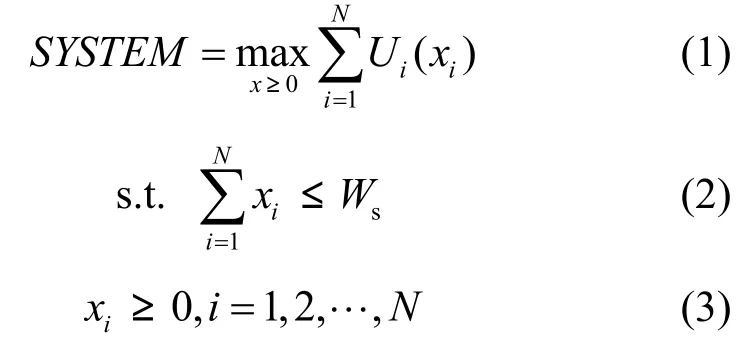
式（1）～式（3）组成的是一个非线性规划问题，对于此类问题在特定条件下是可解的（目标函数是一个严格的凹函数，约束条件是凸集）。但是目标函数中的效用函数 Ui(⋅)是各个节点的私有信息，资源节点并不拥有该信息。考虑到P2P网络的分布特性，该模型应用到P2P网路中求解时必须对上述问题进行分解和转换。

2.2 问题分解

结合整个网络中分为资源节点和请求节点这一特点，本文应用优化的标准方法拉格朗日对偶理论将上述问题分为2部分处理，即资源节点和请求节点，并通过梯度法更新拉格朗日乘数求解整个问题。

假设请求节点i为了获取带宽资源 wi向资源节点提交竞价 bi≥ 0 ，则获得的带宽资源为 xi(bi)，需要付出的资源代价为 ci( bi)。 ci(⋅)称为支付函数，该函数是连续的、递增的、凸的，表示节点i获取资源 xi(bi)需付出的代价，即在接受资源节点服务时需要保留 ci(bi) 单位的带宽作为自己的上载带宽，以便为其他潜在的请求节点提供服务，由此限制条件式（3）转化为式（6）。通过这种方式使得原来 P2P网络中的无偿获取资源变为有偿获取资源，从而让自私请求节点选择真实的带宽需求，避免了“公共地悲剧”的发生，提高整个P2P网络带宽的有效利用率。

节点提交竞价后，下一步对于资源节点来说就是求解式（1）所示的系统最优化问题，但由于效用函数是各个节点的私有信息，故资源节点无法得到每个请求节点的效用函数。在本机制中采用估值效用函数[10]bilog(xi+ 1 )代替式（1）中的效用函数，则在资源节点处系统最优化问题转化为式（4）至式（6）。

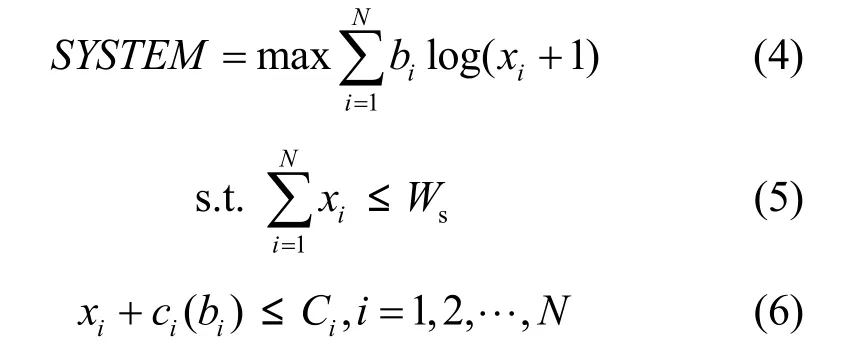
其中， Ci表示节点当前的空闲带宽。

对于上述SYSTEM最优化问题，可以构造如下拉格朗日对偶函数

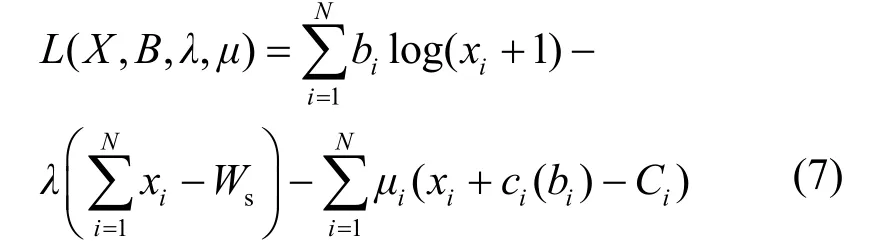
由于 L (X,B,λ,μ)是严格凹的，故由凸优化理论可知上述SYSTEM问题有最优解，且是唯一的。最优解满足如下的库恩—塔克条件

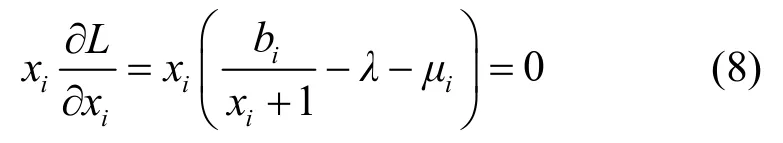
对于式（8）有2种情况。

1) xi= 0 ，此时表示请求节点i给出的竞价为0。

2) xi≠ 0 ，此时表示请求节点i给出的竞价不为0，则得到式（9）

为了将上述2种情况统一，将式（9）修正为

为了求解原问题，还必须知道拉格朗日乘数向量μ以及参数λ，通过原问题的对偶问题就可求解得到。根据拉格朗日对偶理论，对偶方程为

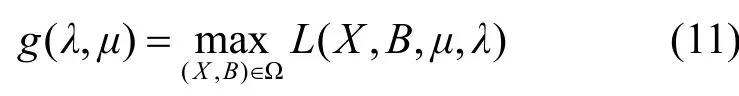
其中，Ω = {(X,B ) ∶xi≥ 0 ,bi≥ 0 }。对应于原问题的对偶问题为

由前一轮的参数已得到当前的B和X，下面计算使得 g (λ,μ)最小化的参数λ和μ。最小化可以通过以下2步计算得到

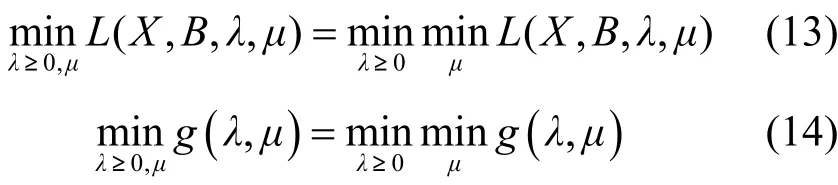
对于给定的 bi(t)和xi(t)，上述对偶问题可以简化为

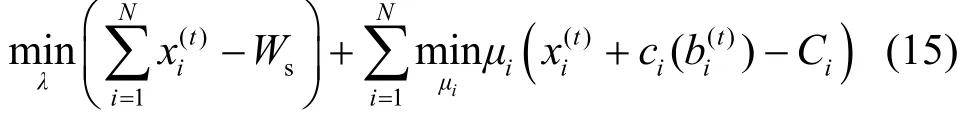
由于对偶函数 g (⋅)可微，则请求节点和资源节点可分别应用梯度迭代法求解式（15），进而求解原问题。运用梯度法按如下方式更新上述参数

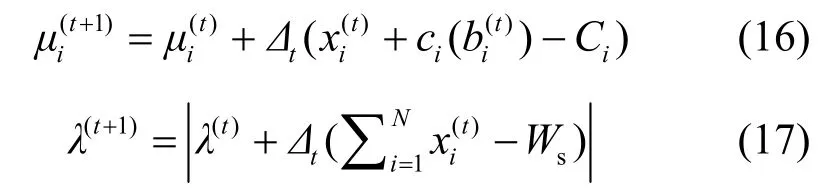
2.3 防止节点欺骗性行为

由于本文的方案是用现有的空闲上载带宽支付获取资源节点带宽的代价，因此会涉及到如何保证节点诚实支付的问题。可能发生如下情况：某个节点为了获取尽可能多的带宽资源，在竞拍时申明比实际能够提供的更大的上载带宽（即竞价）。由于竞价带宽是为潜在需求节点服务，故资源节点无法认证是否如实支付。监测整个P2P网络中节点的行为非常复杂，本文建议采用文献[12]中的日志审计法，将所有请求节点的最终竞价以及资源节点的分配方案记入日志，并发送给区域控制节点（RC）。RC周期性的随机检测某些节点的日志，若发现有欺骗行为，则采取严厉的惩罚措施，如永久性封停该账号。

3 分布式算法实现

由于P2P网络没有中心控制节点，故本文设计了一个不依赖于中心节点的分布式算法。该算法通过梯度法更新拉格朗日参数μ和λ。对于资源节点，当前分配方案带宽总和大于 Ws时增大λ，反之则减小λ；对于请求节点，当分配到的带宽小于需求带宽 wi时提高竞价 bi，但需满足，反之则降低竞价 bi。该算法指导请求节点选择带来最大收益的竞价，并最终使得分配方案趋于稳定。令t表示迭代轮数， bi(t)表示节点i在t轮迭代时给出的竞价， μi(t)是节点i在t轮迭代时给出的参数，λ(t)是资源节点在t轮迭代时给出的参数，为资源节点在t轮迭代时给出的资源分配方案。下面是基于拍卖的分布式带宽分配（AB-DBA）算法的具体描述。

1) 初始化参数。令 t = 0 ，资源节点初始化参数 λ(0)，各请求节点初始化参数 μi(0)、ws和竞价 bi(0)，并将竞价提交给资源节点。

2) 资源分配。资源节点接收到各个请求节点的竞价 bi(t)后，依据式（10）调整带宽分配方案 X(t)，即

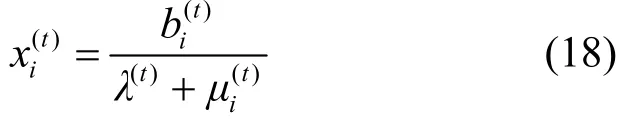
3) 调整参数。资源节点和请求节点根据当前的带宽分配方案 X(t)，运用梯度下降法调整参数λ和μi

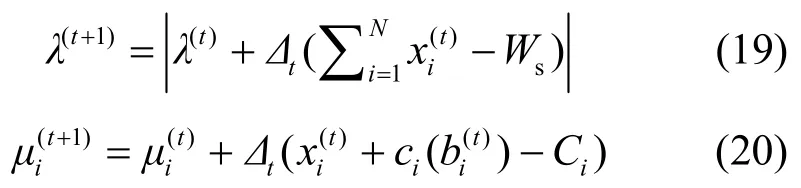
4) 调整竞价。请求节点i依据当前的 X(t)调整下一轮的竞价。若 x(t)= w ，则竞价不变；若i sx(t)＜w，则依据式（21）提高竞价；若x(t)＞w，i si s则依据式（22）降低竞价。

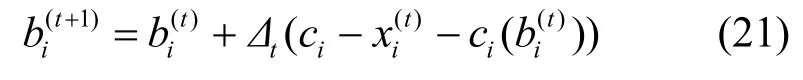
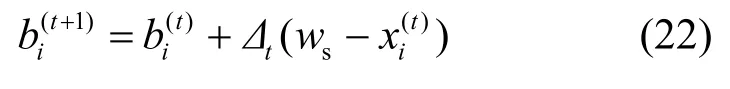
该方案正确运行时存在一个假设，即所有请求节点与资源节点交换信息必须是同步进行的，但是可以利用文献[13]中的方法将其转化为异步方式。由凸优化理论可知，当目标函数是可微的并且是严格凹时，上述算法一定是收敛的。上述方案中的迭代步长依据文献[14]选取。

将该算法应用于实际的P2P网络中时，需要在请求节点与资源结点之间传递的信号包括拉格朗日乘数μ、λ、竞价向量B和资源分配向量X，其中，λ实际表示单位带宽资源的价格。资源节点根据请求节点的需求调整该价格，起到类似市场经济中的价格杠杆作用，从而达到合理分配资源的目的。

4 仿真实验

4.1 实验设置

OMNeT++[15]是基于 C++的离散事件仿真平台，它可以用来仿真通信网络、多处理器系统和其他分布式并行系统。本文基于 OMNeT++平台上的Swarming内容分发仿真模块实现了本文设计的P2P内容分发网络资源分配算法。

在本文的仿真模型中，只有一个内容源服务器。为了更接近现实中接入带宽的异质性，设置了多类节点，它们具有不同的接入带宽，如表1所示。

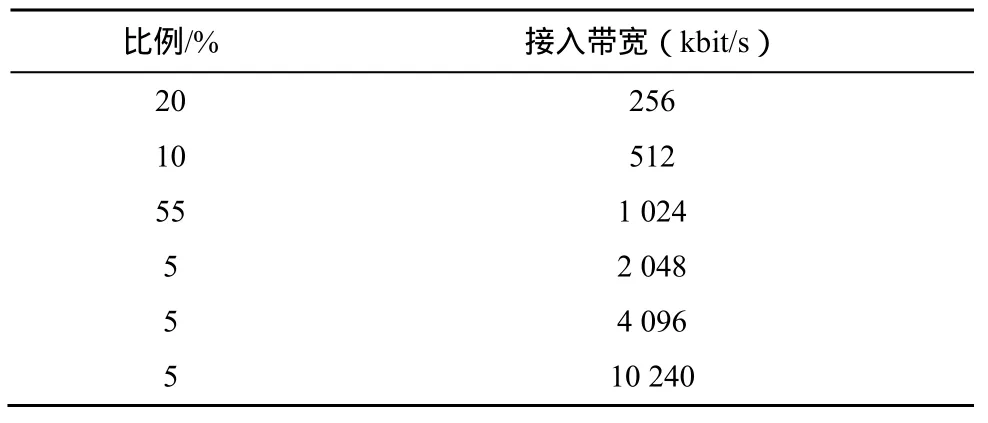
表1 节点信息

在仿真模型中，源服务器的上下载带宽为10Mbit/s。每个数据块大小为 256kbit，整个数据文件为100MB。

为了验证本文提出的基于拍卖机制的P2P网络带宽分配机制的性能以及AB-DBA算法的收敛性，进行了如下2组实验，第一组为实验1和实验2，主要验证AB-DBA算法的收敛性，第二组为实验3至实验5，验证AB-DBA算法对系统性能的影响，其中主要与文献[5]中的“tit-for-tat”机制以及随机资源分配机制相比较。实验数据初始化设置如下，本实验采用动态迭代步长 Δt=1.0/t，可以达到前期快速逼近，后期随着迭代步长的变小，缓慢逼近，提高精确度。其他参数初始化值分别为ε=0.01，，即初始出价为节点空闲带宽的20%。

4.2 实验结果

实验 1 节点给出真实竞价时的资源分配及收敛情况

在实验1和实验2中，选了系统中4类具有代表性的节点，接入带宽分别为256kbit/s、512kbit/s、1 024kbit/s、2 048kbit/s，这4类节点占到整个系统的90%。由于整个系统由多个拍卖组组成，为了简单清晰地显示拍卖的收敛过程，选取系统中局部的一个拍卖组，该组由5个节点组成，分别为1个拍卖执行者和4个竞拍者，拍卖执行者的可拍卖带宽为2 048kbit/s，4个竞拍节点为ND-256、ND-512、ND-1024和ND-2048，空闲带宽分别为256kbit/s，512kbit/s、1 024kbit/s和 2 048kbit/s。

如图1和图2所示，在空闲带宽不同的情形下，各个节点依据自己的带宽需求及自己空闲带宽调整自己的竞价，最终系统达到平衡。依据图1可知，节点ND-256、ND-512、ND-1024和ND-2048获得的下载带宽分别为136kbit/s、273kbit/s、546kbit/s、1 092kbit/s。而此时它们的竞价由图 2可知分别为121kbit/s、241kbit/s、483kbit/s和 967kbit/s。可见竞价越高，即愿意提供的上载带宽越多，获得的下载带宽也越多，且两者成比例，体现了资源分配的公平性。由图可知，该算法在迭代 18次左右可趋于稳定，收敛速度较快。

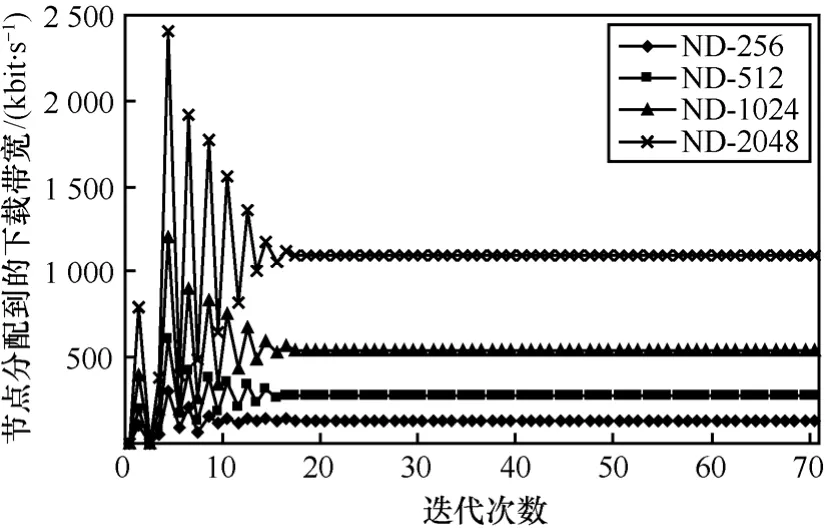
图1 节点资源分配情况

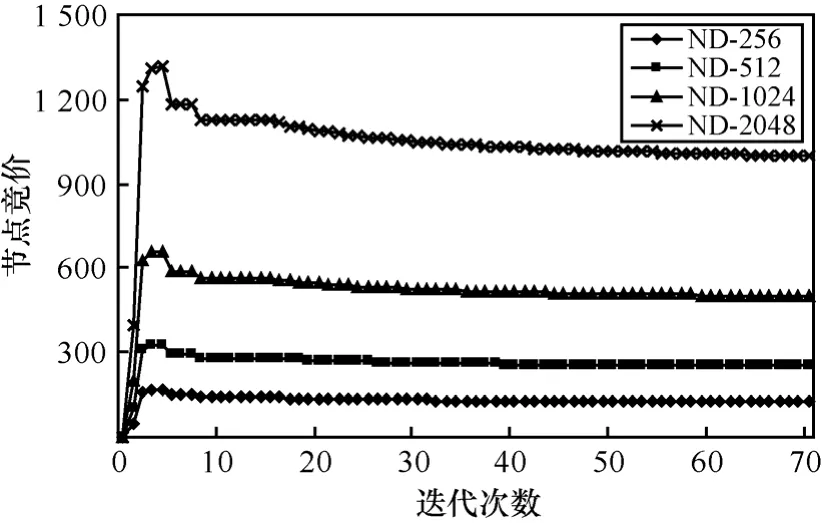
图2 节点竞价情况

实验2 存在自私节点时资源分配及收敛情况

如图3所示，自私节点在前30次迭代时提供的都是真实竞价。而第 31次迭代开始，节点ND-1024企图保留0单位的上载带宽获取资源，即不提供服务给潜在的节点，此时该节点立即遭到本机制的惩罚，分配到的资源为 0。系统经过若干轮迭代后再次达到平衡状态。由于其他3个节点之前并没有获取到全部需求的带宽资源，故当一开始分配给节点ND-1024的资源释放后，其他节点分配到的资源自然上升，表明即使有自私节点存在也不会影响其他节点的正常资源分配。这显示了本机制能够有效遏制搭便车现象的发生，具有使节点合作的强制性。

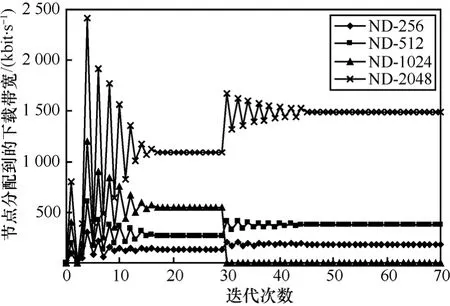
图3 包含自私节点时的资源分配情形

实验3 节点获取内容平均完成时间

图4中，TIT-TAT表示BitTorrent中的资源分配机制，RND表示随机资源分配，AB-DBA表示本文提出的资源分配机制。从图中可知，不管哪种机制，随着节点数的增加，节点获取内容的平均完成时间都会随之增加。这是由于节点具有自私性，节点的带宽设置通常是上载带宽小于下载带宽，故随着节点的增加，上载带宽供需矛盾越突出。TIT-TAT和RND机制并没有处理好该供需矛盾，故随着节点的增加，获取内容的平均完成时间大幅增加。而运用 AB-DBA机制的平均完成时间与这 2种机制相比具有明显优势，在节点数为100时，分别比TIT-TAT和RND机制减少40%和55%的时间，而在节点数为500时，更是减少55%和70%。说明该机制能够通过浮动的带宽价格调节系统中上载带宽的供需关系，当上载带宽资源紧缺时，迫使节点获取同样的资源时需要贡献更多的上载带宽，避免“公共地悲剧”发生。

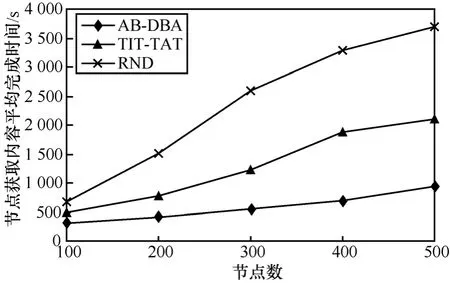
图4 不同资源分配机制中节点获取内容的平均完成时间

实验4 系统中上载带宽与总带宽之比

由图5可知，采用随机资源分配时，系统上载带宽与总带宽的比值在0.1附近波动，总体呈现上载带宽极度匮乏的局面，有时甚至逼近 0，此时上载带宽枯竭，即产生“公共地悲剧”，严重影响整个系统的性能及用户体验。采用TIT-TAT资源分配策略时，起初上载带宽与总带宽的比值在(0.4,0.6)区间内，说明上载带宽供需处于较为合理水平，但随着时间的推移，系统中产生一些特权节点，这些节点具有较高的接入带宽，可以获得优质的服务，造成接入带宽较小的节点失去贡献资源的动力，从而造成整体上载带宽资源的逐步减少，系统性能下降。而本文提出的AB-DBA资源分配机制上载带宽与总带宽的比值虽然有一定波动，但是总体平稳，且基本维持在(0.4,0.6)区间内，表明系统中上载带宽与下载带宽比达到一个较为平衡的状态，提升了整体系统的性能，由图4中的节点获取内容平均完成时间可以验证。

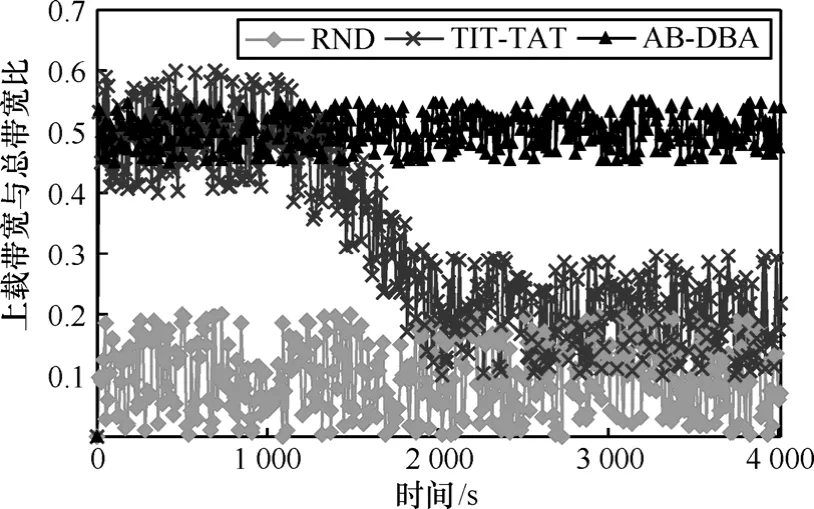
图5 系统上载带宽占总带宽比

实验5 源服务器上传数据比例

由图6可知，随着节点数的增加，源服务器上传数据占总数据量的比例趋于稳定，即 RND机制中源服务器上传数据比在50%以上，TIT-TAT机制中源服务器上传数据比在25%左右，而本文提出的AB-DBA机制中源服务器上传数据比例在 15%左右，具有一定的优势。显然，当总的下载数据量相对固定时，源服务器上传数据比例越低，则其他节点贡献的资源越多，从侧面表明该系统中自私节点数量越少，系统的可扩展性也越好。这表明AB-DBA机制能够遏制节点的自私性行为，提高系统的可扩展性。

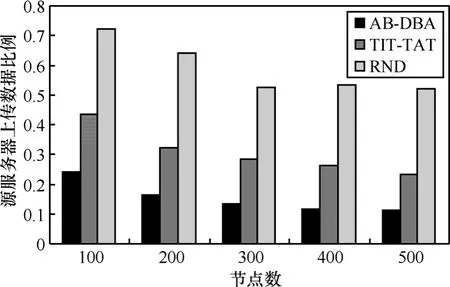
图6 源服务器数据上传比例

5 结束语

P2P内容分发网络中存在大量自私节点希望无偿使用网络资源，从而造成网络资源匮乏且分配不合理，甚至导致“公共地悲剧”的发生。为了解决上述问题，本文利用微观经济学中的拍卖模型对P2P内容分发网络中的带宽分配问题进行建模，通过请求节点保留部分上载带宽以获取资源节点的下载带宽的支付方式，构建了一种基于拍卖的P2P带宽分配机制。仿真结果表明，该机制可以有效遏制节点的自私性行为，避免“公共地悲剧”的发生，保证了可提供服务的上载带宽量，从而缩短P2P内容分发的平均完成时间，降低内容源服务器的上传数据比例，提升了系统的可扩展性。

本文设计的基于拍卖模型的P2P网络带宽分配机制只遏制了需要获取资源的节点的自私性行为，并没有考虑如何激励当前不在享用系统资源的节点主动贡献上载带宽以提高系统的整体性能。作者正在探索该问题的解决方案。

[1] ADAR E, HUBERMAN B A. Free Riding on Gnutella[R]. Xerox PARC, 2000.

[2] HARDIN G. The tragedy of the commons[J]. Science, 1968, 162(3859)∶ 1243-1248.

[3] 刘志新,申妍燕,关新平. 一种基于 VCG 拍卖的分布式网络资源分配机制[J].电子学报, 2010, 38(8)∶1929-1933.LIU Z X, SHEN Y Y, GUAN X P. A VCG-auction based distributed mechanism for network resource allocation[J]. Acta Electronica Sinica,2010, 38(8)∶1929-1933.

[4] RICHARD T B M, SAM C M L, JOHN C S L. Incentive and service differentiation in P2P networks∶ a game theroretic approcach[J].IEEE/ACM Transactions on Networking, 2006, 14(5)∶ 978-991.

[5] COHEN B. Incentives build robustness in BitTorrent[A]. Workshop on Economics of Peer-to-Peer Systems [C]. Berkeley, CA, USA,2003.

[6] KLEMPERER P. Auction theory∶ a guide to the literature[J]. Journal of Economic Surveys, 1999, 13(3)∶227-286.

[7] KRISHNA V. Auction Theory (2nd ed)[M]. Academic Press, USA,2010.

[8] COURCOUBETIS C, WEBER R. Pricing Communication Network∶Economics, Technology and Modeling[M]. Wiley Online Library, 2003.

[9] YANG S, HAJEK B. VCG-Kelly mechanisms for allocation of divisible goods∶ adapting VCG mechanisms to one-dimensional signals[J].IEEE Journal on Selected Areas in Communications, 2007,25(6)∶1237-1243.

[10] KELLY F P, MAULLOO A K, TAN D. Rate control in communication networks∶ shadow prices, proportional fairness and stability[J]. Journal of the Operational Research Society, 1998, 49(3)∶237-252.

[11] BERTSEKAS D P, NEDIC A, OZDAGLAR A. Convex Analysis and Optimization[M]. Nashua∶ Athena Scientific, 2003.

[12] KABUS P, TERPSTRA W W, CILIA M. Addressing cheating in distributed MMOGS[A]. Proc NetGames[C]. New York, NY, USA, 2005.1-6.

[13] BERTSEKAS D P, TSITSIKLIS J N. Parallel and Distributed Computation[M]. New York∶ Prentice Hall Inc, 1989.

[14] BOYD S, VANDENBERGHE L. Convex Optimization[M]. Cambridge∶ Cambridge University Press, 2004.

[15] OMNeT++ community site[EB/OL]. http∶//www.omnetpp.org, 2012.