基于信息传播的社交网络拓扑模型

刘衍珩，李飞鹏，孙鑫，朱建启

（1. 吉林大学 计算机科学与技术学院，吉林 长春 130022；2. 吉林大学 符号计算与知识工程教育部重点实验室，吉林 长春 130012）

1 引言

当前，以人际关系网为基础的社交网络平台日益受到广大网民与商家的追捧，国外的Facebook、Myspace以及国内的人人网、开心网等社交网站迅速发展，用户的规模呈现爆发式增长，拥有大量拥趸。据报道Facebook的用户数量已经超过了7.5亿，并且每天至少有大约 50%的用户登录 Facebook；2010年3月， Facebook的访问流量占当月全美网络流量的7%，而这一比例已超过了Google的访问流量。根据CNNIC测算，截止到2009年底中国使用交友网站和社交网站的网民数已达到1.24亿。社交网络在为用户提供交流信息平台的同时，也具有一些社会功能，例如：社交网络为电子商务的发展带来了机遇，政府机构可以通过社交网络为某个政策的制定征集信息，消费者可通过社交网络对一个品牌及其产品进行评论等。

社交网络正逐渐融入人们的日常生活并发挥着重要影响。快速发展的社交网络不仅为信息的传播与分享提供了新的平台，而且成为用户展示自我价值、表达利益诉求和维护人际关系的重要途径，因此，掌握社交网络的用户特征及其行为，分析社交网络信息传播的内容、特点、传播方式及传播效果具有重要的理论价值和现实意义。

然而，考虑到社交网络庞大的规模和复杂的拓扑结构及安全问题，直接将某个社交网络平台作为实验对象进行研究和分析是十分困难的。因此，研究者试图根据真实网络数据和网络所具有的关键特征对社交网络拓扑结构进行模型抽象，从而以拓扑模型代替社交网络，通过拓扑模型认识社交网络的基本特性并进行相关研究。同时，对社交网络拓扑建模的研究有利于深刻理解人类信息交流的过程。

利用建模的方式研究网络结构和行为的方法由来已久。早在20世纪60年代，Paul Erdos和Alfred Renyi[1]就提出利用随机图理论来分析网络结构的拓扑复杂性，他们构建的网络模型被称为“ER模型”；1998年Watts和Strogatz[2]在Nature上发表的论文中提出了“小世界网络”模型即WS模型，该模型的主要贡献是提出了介于规则网络和随机网络之间的小世界网络，并能通过重连概率p进行调节，从而可使网络结构在规则网络和随机网络之间转化；在Falatous等[3]提出了Internet的度分布具有幂律特性之后，无标度网络便成为了研究者关注的主要对象。Barabasi和Albert对已有的网络模型进行分析后发现许多模型都没有考虑到实际网络所具有的2个重要特性：增长特性和择优连接特性；基于以上2个特性，Barabasi和Albert[4]于1999年提出了一个无标度网络模型，并举例说明许多实际网络都具有所谓的“无标度性”；随着对复杂网络无标度特性研究的深入，学者们发现社交网络也具有明显的无标度特性，Ebel等[5]最先研究了电子邮件网络的无标度特性，他们建立的电子邮件网络模型是典型的无标度网络模型，其出度与入度的幂律指数分别为-2.0和-1.5；Kumar等[6]在对拥有 500万用户的某在线交友网络的数据进行分析后，提出了一种网络生长模型用以分析网络的结构演化过程；Backstrom等[7]在对从Live Journal上采集到的有关用户间所建立的朋友网络原始数据进行分析后发现个体加入社区的偏好以及社区的生长速度都以微妙的方式依赖于网络的底层结构；Leskovec和 Horvitz[8]利用微软 Messager即时通信系统采集的数据构建了一个无向网络模型，通过分析模型的结构发现人们倾向于与自己年纪相仿、语言相通或地区相近的人进行沟通，并且异性间的通信要远比同性间的通信更频繁和持续时间更长；Centola[9]通过研究在线社区上健康行为的传播特点分析了网络结构对行为传播的影响作用，分析结果表明行为在具有较好集群结构的网络中传播得更快、更远；孙鑫等[10]从社会工程学的角度研究了社交网络蠕虫的传播机制，通过将影响用户行为的若干因素进行量化，提出了微观节点上的基于用户安全意识的行为博弈模型，并且通过分析网络用户活动的习惯特性，构建了宏观网络上离散的基于用户习惯的社交网络访问模型。

以上模型大多数仅仅给出了节点间相互作用存在与否的定性描述，而未能体现出实际网络中节点间相互作用的强度，因而在反映网络性质与功能方面存在一定的缺陷。Yook等[11]在考虑到无权网络的这一缺陷之后，将“边权”这一表征节点相互作用强度、频率等意义的概念引入到网络模型中，于 2001年提出了一个加权的无标度网络模型；针对已有的一些加权网络模型未考虑到模型增长过程中权值的动态演化这一缺陷，Barrat等[12]提出了BBV模型，该模型在综合考虑了网络结构和节点权重等因素的基础上研究了网络的动态演化情况，研究发现随着 BBV模型规模的增大，模型的度、边权值和节点的权重都呈现无标度特性。随着加权网络模型的涌现，越来越多的研究者将目光投向了加权网络。

本研究在综合考虑信息传递的有向特性和信息传递的强度以及频率的基础上，结合信息传播所遵循的规律模拟信息传递的动态过程，通过构造加权有向拓扑模型以更好地仿真社交网络的拓扑结构。

2 信息传播的特点

信息传播具有小范围内有明确指向性、大范围呈网状发散性的特点。在现实生活中，每个人既是信息的接收者又是信息的传播者，而接收和传播信息的媒介主要包括大众媒介和人际网络。随着大众媒介的不断升级与变革，人们通过大众媒介获取和传播信息的途径越来越多，但是不同人群利用大众媒介获取和传播信息的能力是参差不齐的，这也为研究大众媒介对个人接收和传播信息的影响带来了一定的困难。相比于大众媒介，分析人际网络对个人接收和传播信息的影响似乎要容易得多。一般来说，一个人在人际网络中的个人影响力越大，其获得和传播信息的途径也就越多。

已有的一些研究已经对信息在人际网络中的传播特点进行了探讨。Leskovec等[13]为了探究信息在社会媒体中的传播过程及其规律，利用带标记的网络对从 3个在线社交网站中获得的数据进行分析，其结果显示社交网络中存在着大量的三角结构（由网络中的3个节点相互连接所形成的三角形），这些三角结构对于研究信息的传播以及人与人之间的相互关系具有重要的意义。Leskovec等的研究不仅对从在线社交网络中获得的实证数据进行了分析，而且还揭示了人际网络中信息传播的特点，即在人际网络中，人们总是倾向于通过自己的朋友获取信息或是将信息传递给自己的朋友。

社交网络是对现实中人际网络的一个真实反映，因此，社交网络中的信息传播就应该体现人际网络中信息传播的特点。因此，本研究在构建社交网络拓扑模型时，不仅考虑了个体在网络信息传播中的影响力，而且借鉴了Holme等[14]在HK模型中使用的演化规则即TF法则：如果节点v和节点w在演化过程的前一步中已经以择优规则连接了一条边，则在本步演化中，从节点w的邻居节点中选择一个节点与节点v进行连接。TF法则反映了现实生活中普遍存在的“三角推荐”现象，即人们新结识的朋友或喜欢的东西在很大程度上可能是由朋友介绍或推荐的。

3 拓扑模型

3.1 模型简介

本研究在考虑了社交网络中信息传播的有向性和强度的基础上提出了一种加权有向拓扑模型。在所构建的拓扑模型中，每个节点代表社交网络中的一个用户，节点间的有向边表示这2个节点所代表的用户之间存在信息传递，而边的权值反映的则是2个节点间信息传递的强度或频率。节点间有向边的权值越大，表明2个节点间信息传递的强度或频率越大。模型中的节点可能是信息的接收者，也可能是信息的传递者，或者兼具这2种角色。

在描述本文构建拓扑模型的具体过程之前，先介绍模型中用到的如下术语。

1) 节点出度（Odi）：以节点i为起点有向边的条数即为节点i的出度。

2) 节点入度（Idi）：以节点 i为终点有向边的条数即为节点i的入度。

3) 节点度（Di）：节点 i的出度与入度之和即为节点i的度，Di=Odi+Idi。

4) 节点出势（Osi）：以节点i为起点的所有有向边的权值之和即为节点i的出势。

5) 节点入势（Isi）：以节点 i为终点的所有有向边的权值之和即为节点i的入势。

6) 节点势（Si）：节点i的出势与入势之和即为节点i的势，Si=Osi+Isi。

7) 集合Outset和Inset：若节点j是集合Outseti中的一个元素，那么存在节点i指向节点j的有向边，表示为 Outseti={j|wij≠0}；类似地，若节点 j是集合Inseti中的一个元素，那么存在节点j指向节点i的有向边，表示为Inseti={j|wji≠0}。

3.2 模型构建过程

为了使本文构建的模型能够展现不同网络结构的拓扑特征，在模型的构建过程中引入了一个外部参数δ（1≤δ＜k）来控制新节点加入网络后新增有向边的数量，以此来改变网络的拓扑结构。

基于信息传播的社交网络拓扑模型的构建过程包括以下步骤。

1) 初始化

① 初始网络是由 n0个节点组成的全耦合网络，即网络中任意2个节点之间都存在2条方向相反且权值为1的有向边。

② 设定网络中新增边的权值都为1。

③ 设集合Seti表示节点i的邻居节点的集合，即Seti=Outseti∪Inseti；集合 BSeti中存放集合 Seti中所有节点的邻居节点，即BSeti={j | k∈Seti，j∈Setk}。

2) 模型生长演化

在每一个时间步内增加一个新的节点，直到网络规模为N。

① 新节点 i根据网络中已有节点的出势所占比重按概率选择一个节点j与新节点i建立有向连接，选择节点所依据的概率公式为

② 求出集合Seti中各个节点的邻居节点，具体过程为

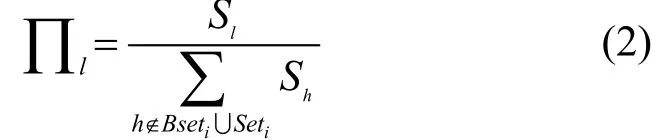
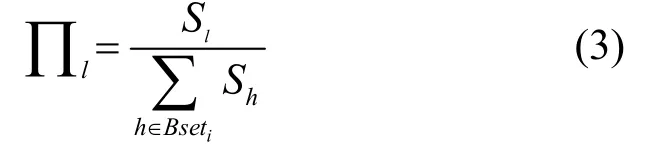
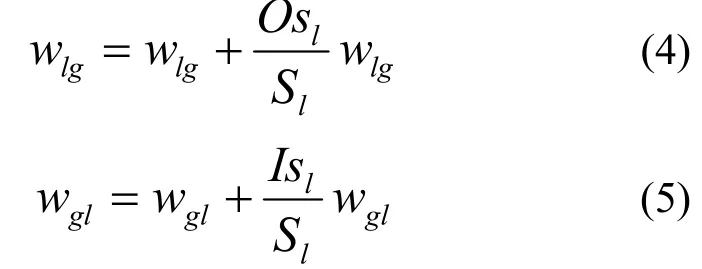
④ 返回步骤②。

考虑到社交网络中一个用户在刚进入网络时，一般倾向于与网络中较活跃的用户进行信息交流，而对于网络中的已有节点，当其出势很大时，通常表明其在网络中是一个很重要的信息源，因此，不论新节点是想从网络中获取信息还是向网络中传播信息，都会倾向于与网络中出势较大的节点建立连接，故而在新节点刚进入网络时，会根据节点出势选择已有节点与其建立连接。

由于模型中边的权值表示节点间信息交流的强度，因此节点的势越大，表明该节点在信息传递过程中的重要性越大，则新节点可通过与该节点建立连接从而迅速融入网络。

3.3 模型描述与分析

通过模型构建的具体过程可以看出，本文在构建模型时综合考虑了个体影响力和现实生活中普遍存在的朋友推荐现象对基于信息传播的社交网络拓扑结构的影响，并且通过引入外部参数δ来调节个体影响力和朋友推荐这2个因素对模型拓扑结构的影响。

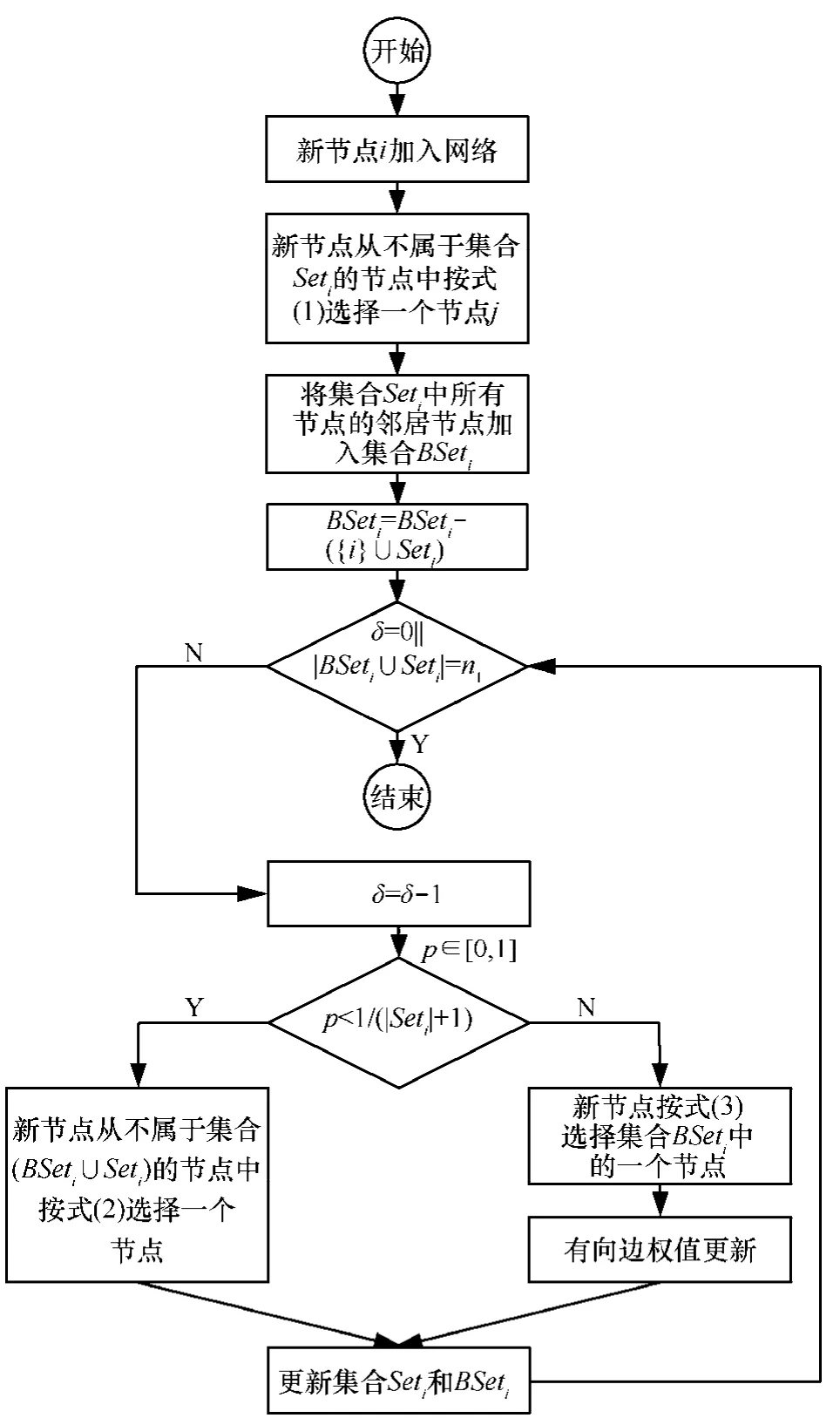
图1 一个时间步内构建模型的流程

如果设定外部参数δ的值为1，那么此时的模型仅考虑个体影响力对社交网络拓扑结构的影响，在网络的每一个生长演化时间步中，新节点根据节点的影响力选择与一个已有节点进行信息交流。

当外部参数δ的值大于1时，模型综合考虑个体影响力和朋友推荐这 2个因素对社交网络拓扑结构的影响。当一个新节点i进入网络后，首先会根据节点的影响力选择与一个已有节点 j进行信息交流；接着，新节点可能会再次从网络中选择一个影响力较大的节点k与之进行信息交流，或者新节点会接受与之通信的节点j的推荐，进而从节点j的邻居节点中选择一个节点进行通信；若演化时间步还未结束，新节点i还是会进行类似的上述过程，即通过已有节点的个体影响力或朋友推荐选择与一个节点交流信息，区别在于：随着演化过程的不断进行，新节点i的邻居节点在不断地增加，其获取信息或传播信息的途径相应地也就增多了，新节点可能不需要与个体影响力大的节点建立连接就能获取或传播足够的信息。而这一现象在模型中体现在模型的每一个演化时间步中，新节点选择与个体影响力较大的节点建立连接的概率在不断地减小。

下面具体分析模型中节点的度和节点的势在演化过程中可能发生的变化。

由模型的构建过程可知，当一个新节点i进入网络后，对于网络中已有的节点 j，可知其度值和势值受以下4个因素的影响。

1) 节点j在演化步骤①中被选中与新节点i建立连接，则其度值增加1，势值增加1。

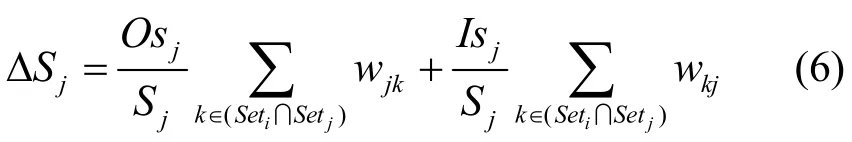
因此，一个时刻节点j的势Sj的变化为

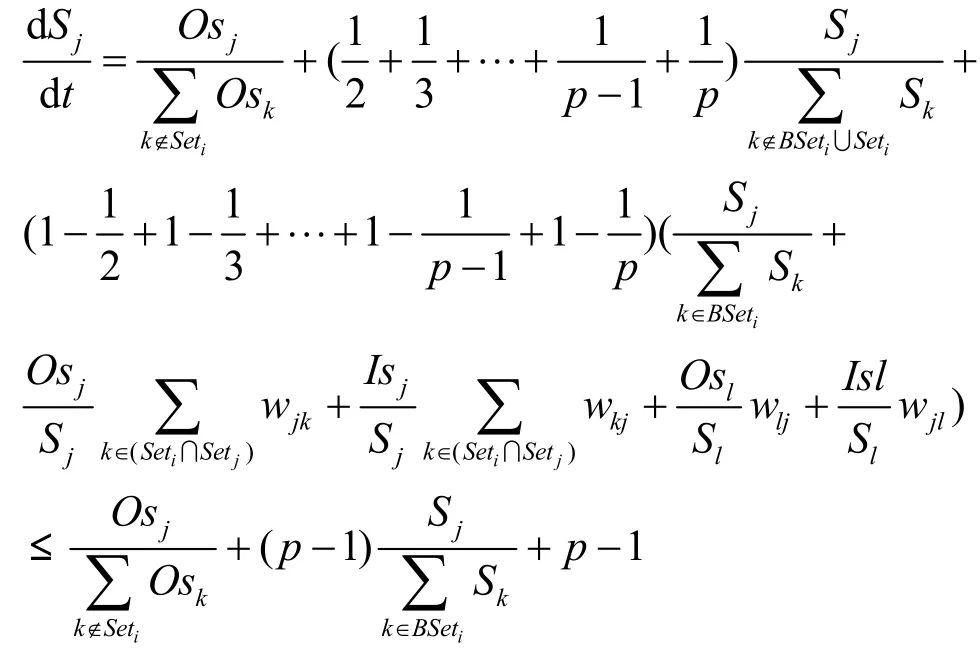
节点j的度Dj的变化为

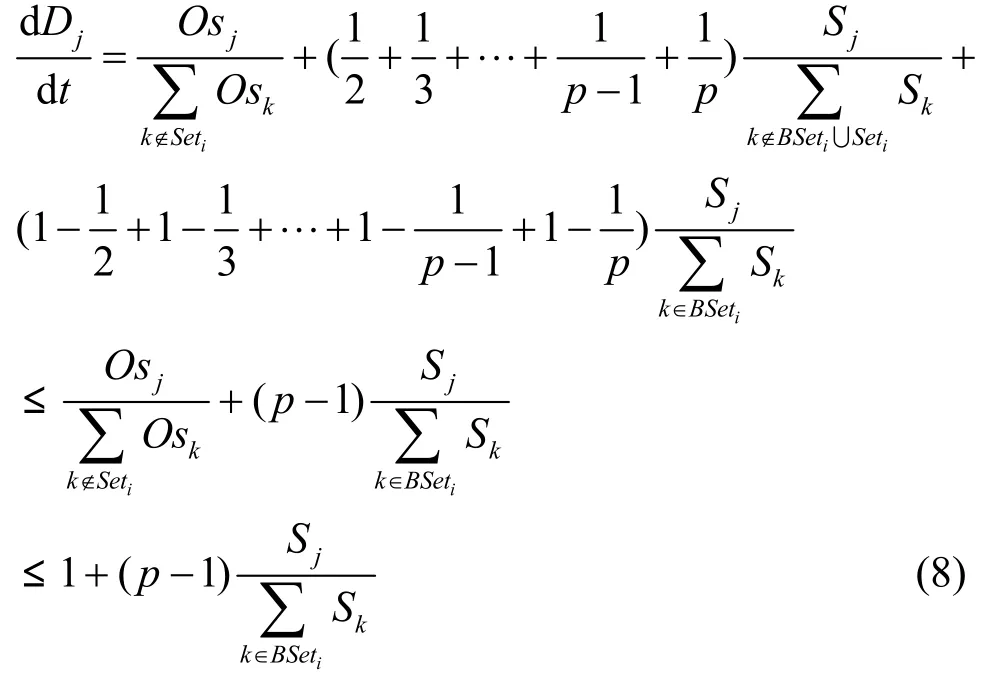
通过上述对某一时刻节点的度和势变化的数学分析（如式(7)和式(8)所示）可知，模型中节点的度分布和势分布是与参数p相关的，而由模型的具体演化过程可知参数 p的值是由外部参数 δ决定的，因此，可通过设定不同的δ值来改变模型中节点的度和势分布。

4 仿真实验

为了验证所构建的网络模型的有效性，本文利用多个评估参数对所生成网络的拓扑结构进行分析。在仿真实验中，设定初始网络规模n0=5，最后生成的网络规模为N=5 000。

实验中通过对比不同δ值下的节点度分布来分析外部参数δ对网络拓扑结构的影响。从图2中可以发现，对应不同的δ值，网络的节点度分布是不同的。当δ=1时，节点度分布服从指数为-2.35的幂律分布，此时的网络实际上就是以节点出势为衡量指标的择优模型；当δ=5时，网络的节点度分布服从指数为-2.73的幂律分布，此时的网络主要从已连接节点的邻居节点中选取节点。

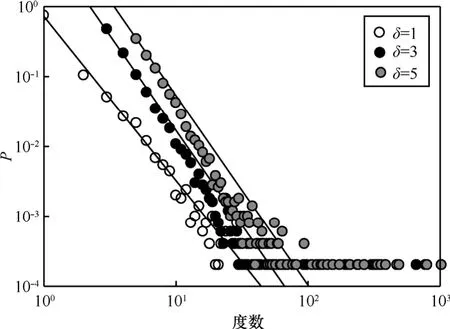
图2 不同δ所对应的节点度分布情况

在以下的仿真实验分析中，本文不再赘述不同δ值对网络拓扑属性的影响，而是设定δ=3。

4.1 节点度分布

实验中首先对模型中节点的度值分布进行研究。通过对实验数据的分析，发现本文所构建的社交网络模型中的节点出度和节点入度的分布都是服从幂律分布的，在对节点出度值和入度值的分布情况进行线性拟合后，发现节点出度服从幂指数为-2.19的幂律分布，节点入度服从幂指数为-2.16的幂律分布。图3表明了节点出度和节点入度在双对数坐标下的具体分布情况。

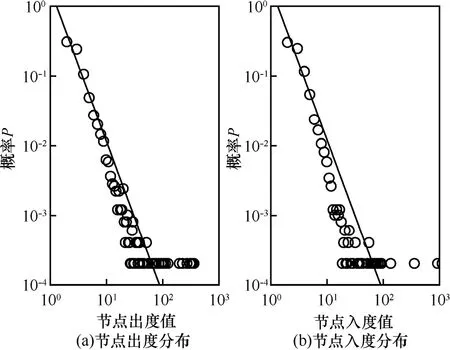
图3 节点出度和入度在双对数坐标系下的分布情况

4.2 节点势分布

通过仿真实验发现，不仅是网络中节点的出度与入度服从幂律分布，节点的出势与入势也是服从幂律分布的。在对节点出势值和入势值的分布情况进行线性拟合后，发现节点出势服从幂指数为-2.44的幂律分布，节点入势服从幂指数为-2.45的幂律分布。图4表明了节点出势和节点入势在双对数坐标下的具体分布情况。

4.3 度—势相关性

既然节点的度值与势值都服从幂律分布，那么节点的度值和势值之间是否也存在某种关联呢？对度—势相关性最早的研究是由 Barrat[15]等完成的。Barrat等在研究了大量实际网络数据集的基础上，发现加权网络中节点的度值与势值是存在幂律关系的，若用s表示节点的势，k表示节点的度，则节点的度值与势值的幂律相关性可以表示为

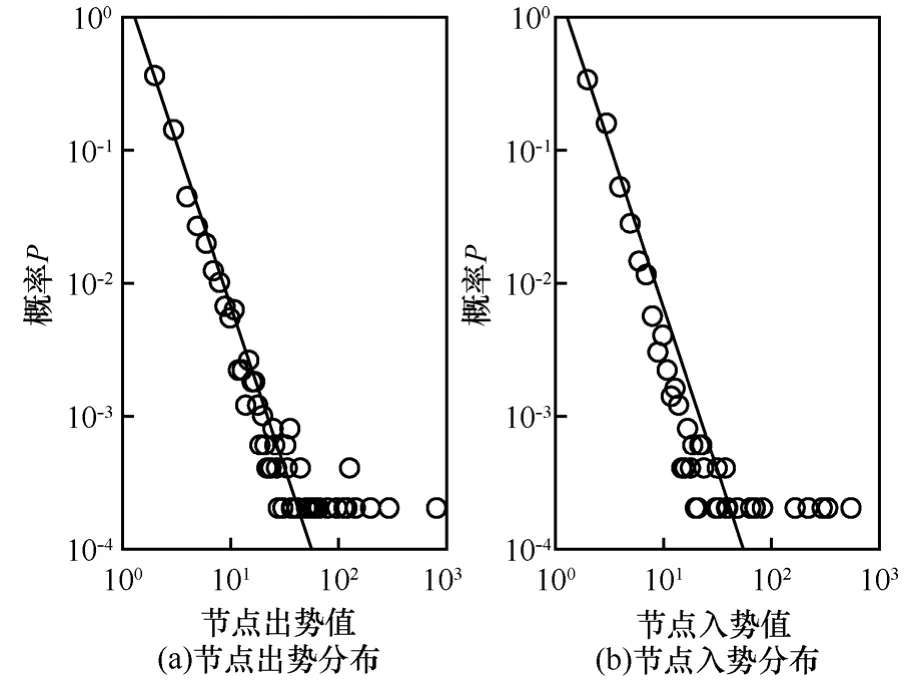
图4 节点出势和入势在双对数坐标系下的分布情况

Barrat等总结出幂律指数 β的值一般是介于1～2之间的。

本文对节点的度—势相关性进行了研究。通过对仿真实验得到的有关节点的度值与势值的数据进行线性拟合分析后发现，节点度值与势值之间的确是存在幂律关系的，图5(a)表明了节点出度与出势的相关性，其中，直线是经过线性拟合后得到的，其斜率为1.09；图5(b)表明了节点入度与入势的相关性，其中，直线也是经过线性拟合后得到的，其斜率为1.18，与实证数据相符[15]。

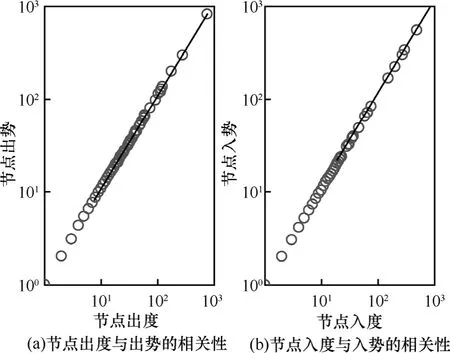
图5 节点度势相关性

4.4 聚集特性

随着对网络拓扑的进一步研究，人们发现仅用节点度的分布来刻画网络拓扑结构是远远不够的，满足同样幂律分布的网络完全可以呈现截然不同的拓扑结构。在幂律分布特性的基础上，人们开始研究网络拓扑中存在的聚集特性。聚集特性是反映网络节点关联性[16]的特性之一，并通过计算网络的聚集系数来反映网络的聚集特性。常用的计算无向图的聚集系数的公式为

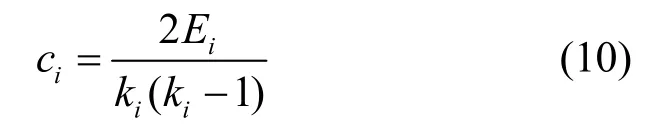
其中，ci表示节点i的聚集系数值，ki表示节点i的度值，Ei表示节点i的邻居节点间存在的连接数。

本文在探讨了节点度与势分布的基础上，对网络的聚集特性也进行了分析。由于节点的聚集系数是用来刻画一个节点与邻居之间的亲疏程度的，即对于一个节点而言，只要其邻居节点间在网络拓扑图中存在连边，则认为其邻居节点间是存在信息交流的，而不用考虑邻居节点间连边的具体方向，因此，在计算节点的聚集系数时是不需要考虑网络的有向性的。本文在计算节点的聚集系数之前，先对加权有向模型进行了无向化处理，然后再利用式(10)进行计算。具体的无向化处理方式为：对于网络中的节点i和节点j，只要wij和wji中有一个不为0，则令邻接矩阵A中Aij和Aji的值为1。图6表明了节点聚集系数与度数的关系，图6(a)中直线是经过线性拟合得到的，其斜率为-0.97。同时，本文还计算了网络的平均聚集系数，其值为 0.312，该值与Newman M E J对一些社交网络的平均聚类系数所做的统计相吻合。

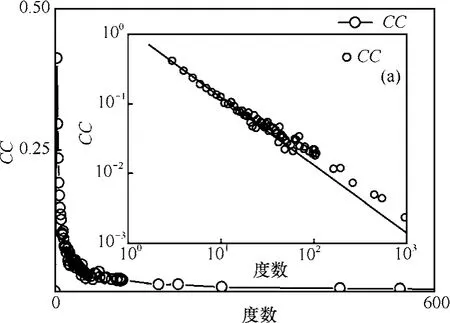
图6 聚集系数与度数的关系

4.5 网络层次性

为了研究社交网络自发的多层次性质，以核数[17]概念为基础，利用本文提出的社交网络模型对网络的层次性做定量分析，这不仅可以细致地刻画社交网络的特征，而且可以全面地描述网络拓扑结构。

若一个节点存在k-核，而在(k+1)-核中被移除，则称这个节点的核数为 k；其中，k-核是指原始图经过迭代消去所有节点度小于或等于k的节点后得到的子图。一个核数为k的节点可以出现在k核子图中，但不会出现在(k+1)核的子图里，笔者把所有节点核数中的最大值称为图的核数。

节点核数在某种程度上是比节点度数更能反映关联性的度量指标，可以表明节点在核中的深度。若一个节点的节点度数很高而节点核数很小，则说明其关联并不紧密。例如，在具有N个节点的星形网络中，其中心节点的度数为N-1，而核数为0，此时，它与邻居节点的连通性易于破坏。

图7表明了本文构建的社交网络模型中节点的核数和度数的关系，图7中直线是经过线性拟合得到的，从图7中可以发现当节点度小于100时，节点核数和度数呈现幂律关系，当节点度大于100时，节点的核数基本保持不变。

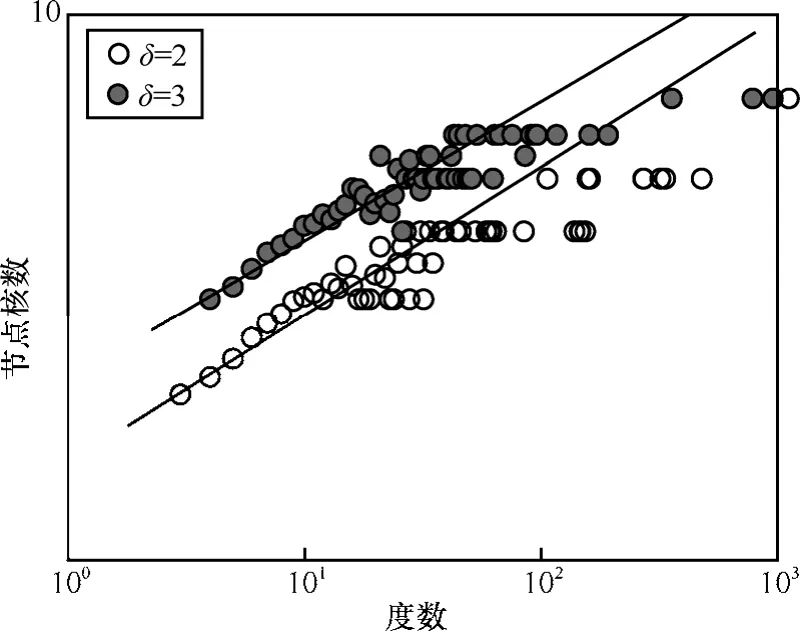
图7 节点核数与度数的关系

4.6 网络异质性

网络异质性是指网络中节点的属性不是大致相同的，而是存在着很大的差异。近年来的研究发现，绝大多数复杂网络都呈现出极强的异质性[18]。以节点的度值分布为例，在绝大多数网络中，节点的度值服从幂律分布，该幂律关系表明：网络中节点的度值分布并不像想象中的那样是均匀分布的，而是极其不均匀的，极少数节点的度值很大，而绝大多数节点的度值很小。为了定量地研究网络的异质性程度。本文利用经济学中描述收入分配程度不均的2个重要概念：洛伦兹曲线和基尼系数，来分析本文构建的社交网络模型的异质性。通过仿真实验发现洛伦兹曲线和基尼系数在分析网络拓扑结构的异质性方面具有很好的效果。

复杂网络的洛伦兹曲线和基尼系数[19]是如下定义的：设一个复杂网络具有 N个节点，记为 v1,v2,…,vN，将这 N个节点按照度值由小到大进行排序，将相应节点的度值记为则显然有对于即

复杂网络的洛伦兹曲线是以累计节点数除以总节点数为横轴，以累计度值除以总度值为纵轴所建立的直角坐标系中的一条曲线曲线（如图8中的曲线OED）。将基尼系数定义为图8中的曲线OED与直线OD之间的面积（用A表示）和三角形OCD的面积（A+B）的比值定义为基尼系数G，即

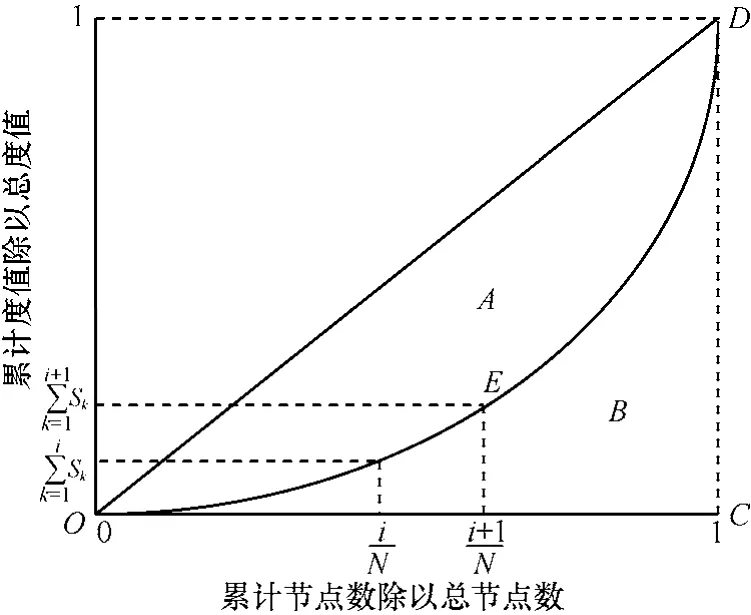
图8 复杂网络的洛伦兹曲线

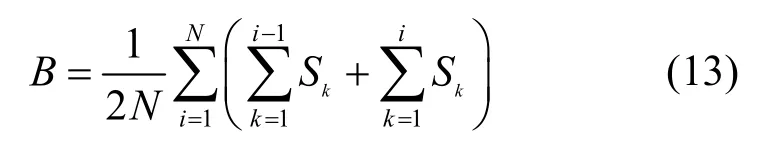
由于三角形OCD的面积为1/2，故可以得到复杂网络基尼系数的计算公式为

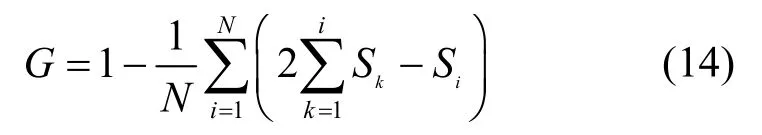
通过复杂网络基尼系数的计算公式（式(14)）可知：0≤G≤1，并且G的值越大，表明网络的异质性程度越大；G的值越小，则表明网络异质性程度越小。由此可见，通过计算复杂网络的基尼系数可以定量地衡量网络的异质性程度。

本文从节点度值与势值这2个方面对所构建的社交网络模型进行了异质性分析。节点度值的异质性分析结果显示：相比于节点入度，节点出度的异质性较小，其基尼系数为 0.496，如图 9所示。对节点势值的异质性分析也得到了与节点度值相似的情况，在此不再赘述。

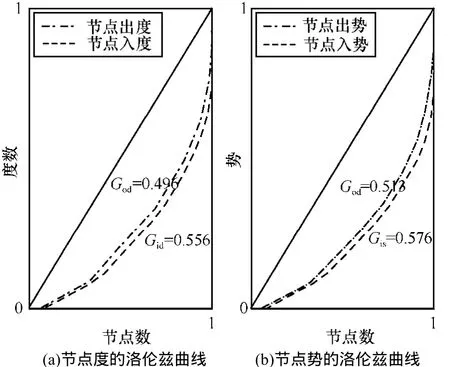
图9 洛伦兹曲线和基尼系数

5 结束语

本文探究了信息在人际网络中的传播特点，基于信息传递的有向特性，通过构造加权的有向拓扑模型模拟了信息传递的动态性，更好地仿真了社交网络的拓扑结构。利用该模型构建了社交网络拓扑，从度、势分布、度—势相关性、网络聚集特性、网络层次性和网络异质性等方面对网络拓扑结构进行了分析。结果表明所生成网络拓扑结构的度、势分布以及度—势相关性具有明显的幂律特性。同时，网络拓扑的聚类系数、核数和基尼系数均表明该模型能够较好地体现社交网络的聚集特性、层次性和异质性。综上所述，本文所构建的网络模型能够正确地体现实际人际关系网络的拓扑结构。

[1] ERDOS P, RENYI A. On the evolution of random graphs[J]. Publication of the Mathematical Institute of the Hungarian Academy of Science, 1960, 5(12)∶17-60.

[2] WATTS D J, STROGATZ S H. Collective dynamics of “small-world”networks[J]. Natrue, 1998, 393(6)∶440-442.

[3] FALOUTSOS M, FALOUTSOS P, FALOUTSOS C. On power-law relationships of the Internet topology[J]. Proceedings of SIGCOMM,1999, 29(10)∶251-262.

[4] BARABASI A, ALBERT R. Emergence of scaling in random networks[J]. Science, 1999, 286 (5439)∶509-512.

[5] EBEL H, MIELSCH L I, BORNHOLDT S. Scale-free topology of E-mail networks[J]. Physical Review E, 2002, 66(3)∶35-103.

[6] KUMAR R, NOVAK J, TOMKINS A. Structure and evolution of online social networks[A]. KDD[C]. New York, USA, 2006. 611-617.

[7] BACKSTROM L, HUTTENLOCHER D P, KLEINBERG J. Group

而折线OED下的面积（用B表示）实际上是N-1个梯形和一个三角形面积的和，即formation in large social networks∶ membership, growth, and evolution[A]. KDD[C]. New York, USA, 2006. 44-54.

[8] LESKOVEC J, HORVITZ E. Planetary-scale views on a large instant-messaging network[A]. Proceedings of WWW 2008[C]. Beijing,China, 2008. 915-924.

[9] CENTOLA D. The spread of behavior in an online social network experiment[J]. Science, 2010, 329(9)∶1194-1197.

[10] 孙鑫，刘衍珩，朱建启. 社交网络蠕虫仿真建模研究[J]. 计算机学报，2011, 34(7)∶1252-1261.SUN X, LIU Y H, ZHU J Q. Research on simulation and modeling of social network worm propagation[J]. Chinese Journal of Computers,2011, 34(7)∶1252-1261.

[11] YOOK S H, JEONG H, BARABASI A L. Weighted evolving networks[J]. Physical Review Letters, 2001, 86(25)∶5835.

[12] BARRAT A, BARTHELEMM Y, VESPIGNANI A. Weighted evolving networks∶ coupling topology and weights dynamics[J]. Physical Review Letters, 2004, 92(22)∶2287011-2287014.

[13] LESKOVEC J, HUTTENLOCHER D, KLEINBERG J. Signed networks in social media[A]. CHI[C]. New York, USA, 2010. 1361-1370.[14] HOLME P, KIM B J. Growing scale-free networks with tunable clustering[J]. Physical Review E, 2002, 65(2)∶1071-1074.

[15] BARRAT A, BARTHELEMY M, PASTOR-SATORRAS R. The architecture of complex weighted networks[J]. The National Academy of Sciences of The United States, 2004, 101(11)∶3747-3752.

[16] NEWMAN M E J. Properties of highly clustered networks[J]. Physical Review E, 2003, 68(2)∶26121-26126.

[17] 周苗，杨家海，刘洪波. Internet网络拓扑建模[J].软件学报，2009,20(1)∶109-123.ZHOU M, YANG J H, LIU H B. Modeling the complex Internet topology[J]. Journal of Software, 2009, 20(1)∶109-123.

[18] KOSSINETS G, WATTS D J. Origins of homophily in a evolving social network[J].American Journal of Sociology, 2009, 115(2)∶405-450.

[19] 王林，戴冠中. 复杂网络的Scale-free性、Scale-free 现象及其控制[M].北京∶科学出版社，2009.WANG L, DAI G Z. Scale-free Property, Scale-Free Phenomenon and Their Control in Complex Networks[M]. Beijing∶ Science Press, 2009.