一类密码函数的构造与分析

欧智慧，赵亚群,2，李旭

(1. 信息工程大学 四院，河南 郑州 450002；2. 数学工程与先进计算国家重点实验室，河南 郑州 450002)

1 引言

密码函数包括布尔函数和多输出布尔函数，它们是构成密码系统的重要组件。特别是在密码算法的非线性实现方面有着重要的应用，在序列密码中，密码函数多用于非线性反馈函数和非线性组合函数环节，在分组密码中多用于实现混乱作用的S盒。因此，对密码函数的研究是分析密码算法的基础性工作，具有十分重要的意义，国内外这方面的研究工作有许多[1~6]。因此，在密码函数的研究中，构造具有良好密码学性质的密码函数十分重要。由于密码函数的各个准则间具有一定的制约关系，构造具有良好密码学性质的密码函数并不容易。Bent函数是一类具有最大非线性度的布尔函数，在抵抗线性攻击方面十分优越，但它有不平衡性、不具有相关免疫性等缺点。2001年，Zheng等[7]提出Plateaued函数的概念，它是一类比Bent函数更广的布尔函数，具有很好的非线性度，可以满足相关免疫性、平衡性，而且可以不具有非零的线性结构，近年来已成为密码工作者研究的热点之一[8~11]。密码函数的各项刻画指标多是应对某种具体的密码攻击而提出的，例如，布尔函数的相关免疫性主要是针对相关攻击提出的，希望布尔函数具有较好的相关免疫性，布尔函数的代数免疫阶主要是针对代数攻击提出的，希望布尔函数具有较高的代数免疫阶。级联构造是一种常用的重要构造方法，形如的布尔函数，就是一种常见的级联构造。通过分析 f (x)和g(x)的密码学性质，得到 h (x,xn+1)的性质。反之，通过分析 h (x,xn+1)的性质，也有利于掌握 f (x)和g(x)的性质。

由于密码算法的设计中更多的是涉及多输出布尔函数，因此，在布尔函数研究相对成熟的基础上，各种研究向多输出布尔函数扩展。一方面，相关概念被推广到多输出布尔函数，如：相关函数、相关免疫性、扩散性、代数免疫性等，进而研究多输出布尔函数的此类性质及具有良好性质的多输出布尔函数的构造。另一方面，布尔函数与多输出布尔函数的关系也是研究的一个重要方面。由于多输出布尔函数的复杂性，关于它的研究，虽然国内外学者也做了不少工作[12~14]，总的来说相关研究并不像布尔函数那么成熟，因此还需做更深入的研究。

孙光洪等[11]通过级联构造了一类布尔函数，详细讨论了此类函数的密码学性质，指出当 f1(x)、 f2(x)、 f3(x)具有较好性质时，f 也具有较好的性质。受文献[11]工作的启发，通过级联t+1个n 元布尔函数，笔者构造了 n+t元布尔函数 G(x,y)，它是文献[11]工作的一般情况。以 Krawtchouk多项式[15]和Krawtchouk矩阵[16]为工具，给出了基函数和G(x,y)谱的确定关系，从而将对 G(x,y)的研究转化为对Krawtchouk多项式和 Krawtchouk矩阵的研究。分析了 G(x,y)的相关免疫性、扩散性和代数免疫性，指出在基函数性质较好的情况下，G(x,y)也具有较好的密码学性质。在特殊情况下，作为Plateaued函数，分析了基函数与G(x,y)的依赖关系。同时，更进一步将构造方法推广到多输出布尔函数，构造了一类多输出布尔函数 H(x,y)，分析了H(x,y)的相关免疫性和代数免疫性。

2 预备知识

记二元域 F ={ 0,1}，n是一正整数，以 Fn表示22n个 F2的笛卡尔积，称 F2n到 F2的任一映射 f (⋅)为n个变元的(Fn上的)布尔函数，即：若记2，则记x的汉明重量为(其中，#S表示集合S中元素的个数)，下面先给出一些基本定义和引理。

定义1[1]设 w ,x ∈F2n，x和w的点积定义为wx设f(x)为Fn2上的布尔函数， w ∈F2n，称为f(x)的Walsh循环谱。

定义2[1]设 f (x)是 Fn2上的布尔函数，如果对任意的，称f(x)为m阶相关免疫的(m阶弹性的)。

定义3[1]设 f1(x)，f2(x)是 Fn2上的布尔函数， s∈F2n， 称为f1(x)和 f2(x)在点 s的互相关系数；称为 f1(x)在点s的自相关系数。

定义4[1]设 f (x)是 Fn上的布尔函数，称 f (x)2满足严格雪崩准则(m阶扩散准则)，当且仅当

定义5[17]设 f (x)是 Fn上的布尔函数2如果对任意的，则称f(x)为r阶Plateaued函数。

引理1[18]设f(x)是 F2n上的布尔函数，则

引理2[15,19]

引理3[19]对于，有，其中，当i=j时,当i≠j时，δi,j= 0 ，称为Krawtchouk多项式的正交性。

3 级联布尔函数G(x, y)的密码学性质

3.1 基函数与G(x, y)的Walsh循环谱关系

下面的引理4和引理6从正反2个方面反映了G(x,y)与其基函数的关系，是考察G(x,y)的密码性质与该性质与其基函数密码学性质关系的基础。

证明 对 s =(α,β)，可得

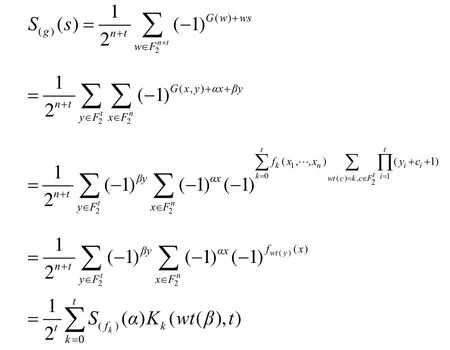
引理5 矩阵 At可逆，且

由引理4及引理5，易得下面的引理6。它是引理4的反演公式。

3.2 G(x, y)的相关免疫性

利用引理2的3)可得定理1和定理2。定理1是引理4的一个应用，这说明在一定条件下，基函数相关免疫性好时 G(x,y)相关免疫性也较好，这为构造高阶相关免疫函数提供了可能。定理2是引理6的一个应用，说明 G(x,y)相关免疫性较好时基函数相关免疫性也较好。

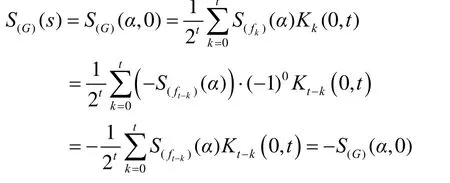
3.3 G(x, y)的扩散性

下面的引理7是分析G(x,y)的扩散性的基础，为方便，记

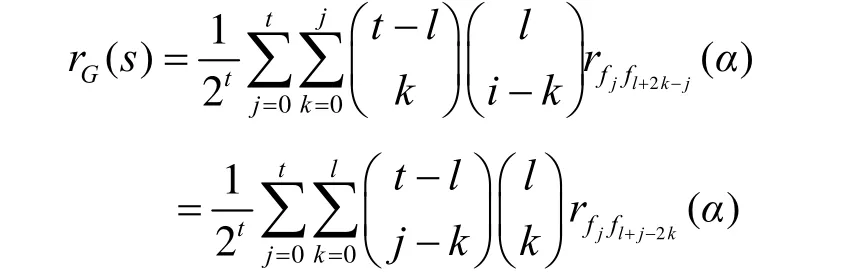
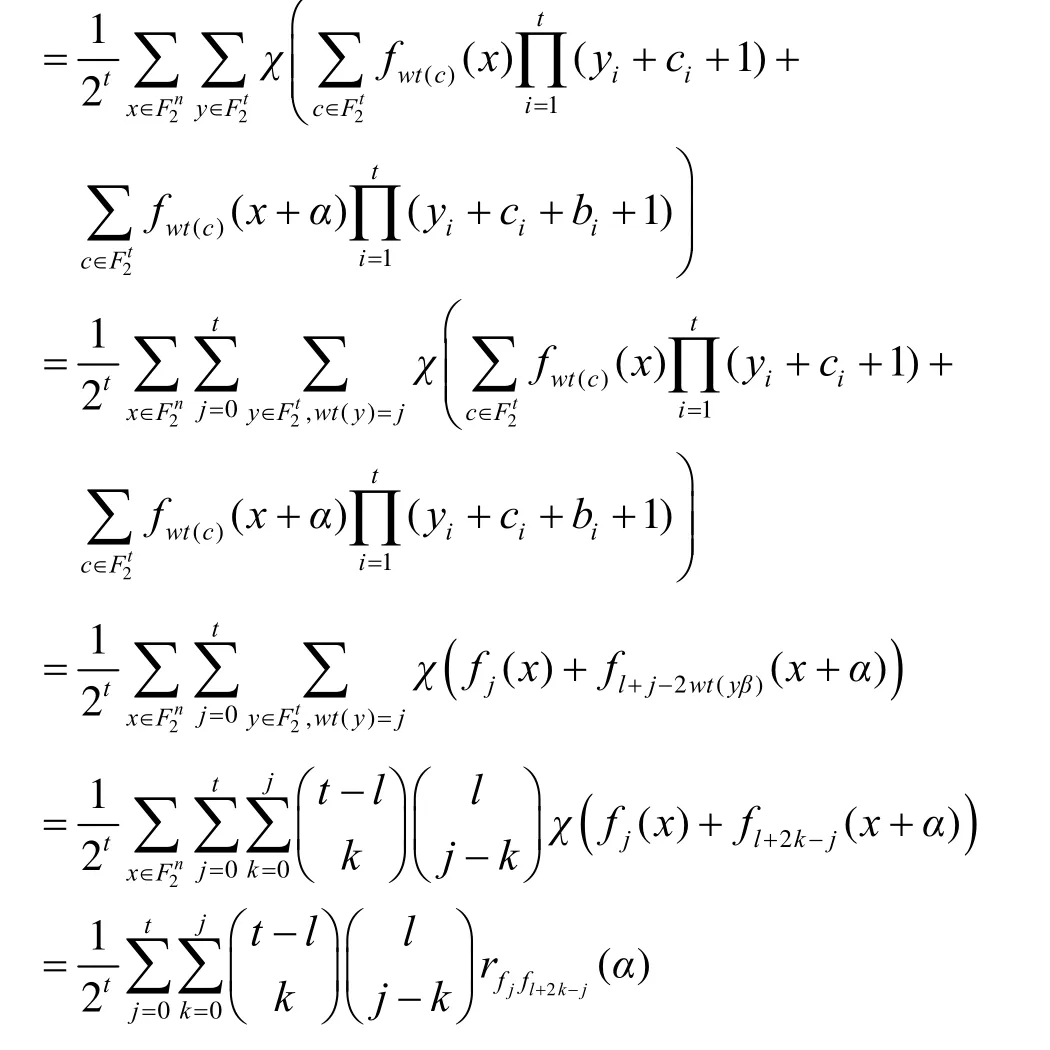
由引理7及推论4可得下面的定理3，它表明在一定条件下G(x,y)满足严格雪崩准则。

满足严格雪崩准则。

3.4 G(x, y)的代数免疫阶

对于 n元布尔函数 f (x)，如果存在布尔函数g(x)使得 f (x)g(x) = 0 ，称 g (x)为 f (x)的零化子。称 f (x)和 f (x)+1的非零零化子的最小代数次数为f(x)的代数免疫阶，记为 A I(f)。

另一方面，设h(x,y)为达到G(x,y)代数免疫阶的布尔函数，则 h(x,y)可表示成如下形式：，其中，为i的二进制表示。如果，则即，取代入上述等式可得，其中，i的二进制表示为；如果同样取，则其中，i的二进制表示为由题设条件知又由，其中

3.5 t=2时G(x, y)的性质

122

2) G是r阶Plateaued函数，对任意 u ∈Fn，

2或，则都是r阶Plateaued函数。

4) 对任意 u ∈Fn，若2，代入式(1)得；若，代入式(1)得且，又由于

是r阶Plateaued函数，故G是r+2阶Plateaued函数。

4 基函数与构造的多输出布尔函数的关系

本节将上述构造推广到多输出布尔函数上，先引入一些基本的定义与结论。

设m，n为正整数且m≤n，称F2n到F2m的任一映射为 (n, m)多输出布尔函数，其中，是Fn2上的布尔函数。

定义 6[1]设 F(x)为(n, m)多输出布尔函数，，称为F(x)的广义Walsh循环谱。

定义7[1]设F(x)为(n, m)多输出布尔函数，，随机向量如果对任意的及有uz与统计独立，则称多输出函数 F (x)是k级j阶相关免疫的。

定义8[20]设F(x)为(n, m)多输出布尔函数，给定输出，若存在n元布尔函数Fy(x)使得任意都有，则称 F (x)为输出y的y状态函数。记 A Iy(F)为输出非零状态函数的代数次数的最小值，当输出y遍历时，称 A Iy(F)的最小值为多输出布尔函数F(x)的代数免疫阶，记为 A I(F )。

引理8[1]设F(x)为(n, m)多输出布尔函数，则F(x)是 k级 j阶相关免疫的充要条件是对任意的及有

类似于引理4和引理6，可以得到下面的引理9和引理10，它们是互为反演的。

利用上面的 2个引理可以方便地讨论基函数与H(x,y)的相互关系，从而构造密码学性质好的多输出布尔函数。作为应用，给出下面的定理6和定理7。

定理6 若任意 Fi(x)是k级j阶相关免疫的，，对于u ∈ F2s+1及任意的，有，则H(x,y)是k级j阶相关免疫的。

5 结束语

通过级联t+1个n元布尔函数构造了n+t元布尔函数 (,)Gxy，将对G(x,y)与基函数的关系研究转化为对Krawtchouk多项式和Krawtchouk矩阵的研究，得到了彼此间循环谱的相互表达式。分析了G(x,y)的相关免疫性、扩散性和代数免疫性。当t=2时，分析了该类函数与基函数作为 Plateaued 函数的依赖关系。同时将上述构造方法推广到多输出布尔函数，通过级联t+1个(n, s+1)多输出布尔函数的分量函数，构造了一类(n+t, s+1)多输出布尔函数H(x,y)。同样利用Krawtchouk矩阵给出了该类函数的广义Walsh循环谱与基函数的广义Walsh循环谱之间的相互表达式。分析了H(x,y)的相关免疫性和代数免疫性。对Krawtchouk多项式和Krawtchouk矩阵的深入研究是进一步分析 G(x,y)和 H(x,y)密码学性质的基础。

[1] 冯登国.频谱理论及其在密码学中的应用[M]. 北京: 科学出版社,2000.FENG D G. Sectrum Theory and the Application in Cryptography[M].Beijing: Publishing Company of Science, 2000.

[2] 何业锋, 马文平. 3类 semi-Bent函数的构造[J]. 电子学报, 2011,39(1):233-236.HE Y F, MA W P. Constructions of three classes of semi-Bent functions[J]. Chinese Journal of Electronics, 2011, 39(1):233-236.

[3] 谢佳, 王天择. 寻找布尔函数的零化子[J].电子学报, 2010, 38(11):2686-2690.XIE J, WANG T Z. Finding the annihilators of a Boolean function[J].Chinese Journal of Electronics, 2010, 38(11):2686-2690.

[4] HU B, JIN C H, SHAO Z Y. Relationship among three kinds of cryptographic Boolean functions with special Walsh spectrum[J]. Journal on Communications, 2010, 31(7):104-109.

[5] MEIER W, PASALIC E, CARLET C. Algebraic attacks and decomposition of Boolean functions[A]. Advances in Cryptology-Eurocrypt 2004[C]. Berlin, Germany, 2004. 474-491.

[6] CLAUDE C. Relating three nonlinearity parameters of vectorial functions and building APN functions from bent functions[J]. Des Codes Cryptogr, 2011, 59(1-3):89-109.

[7] ZHENG Y, ZHANG X M. On Plateaued functions[J]. IEEE Transactions on Information Theory, 2001, 47(3):1215-1223.

[8] 胡斌, 金晨辉, 冯春海. Plateaued 函数的密码学性质[J]. 电子与信息学报, 2008, 30(3): 660-664.HU B, JING C H, FENG C M. Cryptographic properties of Plateaued functions[J]. Journal of Electronics & Information Technology, 2008,30(3):660-664.

[9] 王维琼, 周宇, 肖国镇. Plateaued函数的正规性[J]. 电子与信息学报, 2008, 30(9): 2283-2286.WANG W Q , ZHOU Y, XIAO G Z. Normality of Plateaued functions[J]. Journal of Electronics & Information Technology, 2008,30(9):2283-2286.

[10] CARLET C, PROUF E. On Plateaued functions and their constructions[A].Fast Software Encryption 2003[C]. Lund, Sweden, 2887. 54-73.

[11] 孙光洪, 武传坤. 级联函数的密码学性质[J]. 电子学报, 2009, 37(4):884-888.SUN G H, WU C K. Some cryptographic properties of Boolean functions by concatenation[J]. Chinese Journal of Electronics, 2009, 37(4):884-888.

[12] YING D H, ZHAO Y Q, FENG D G. Correlation functions of mulioutput m-valued logical functions and relation between correlation functions and spectra[J]. Zhengzhou Univ NatSci.Ed, 2007,39(2):21-24.

[13] 王秋艳, 金晨辉. 多输出布尔函数与布尔函数代数免疫阶之间的关系[J]. 电子学报, 2011, 39(1):124-127.WANG Q Y, JIN C H. Relationship between the algebraic immunity of multi-output Boolean functions and Boolean functions[J]. Chinese Journal of Electronics, 2011, 39(1):124-127.

[14] 胡斌, 金晨辉, 史建红. 多输出 Plateaued 函数的密码学性质[J].电子与信息学报, 2009, 31(6):1433-1437.HU B, JIN C H, SHI J H. Cryptographic properties of multi-output Plateaued functions[J]. Journal of Electronics & Information Technology, 2009, 31(6):1433-1437.

[15] MACWILLIAMS F J, SLOANE N J. The Theory of Error-Correcting Codes[M]. North Holland: Elsevier, 1977.

[16] FEINSILVER P, KOCIK J. Krawtchouk matrices from classical and quantum random walks[J]. Contemporary Mathematics, 2007, 287(2001):83-96.

[17] CARLET C. Partially-bent functions[J]. Des Codes Cryptogr, 1993,3(2):135-145.

[18] 丁存生, 肖国镇. 流密码学及其应用[M]. 国防工业出版社, 1994.DING C S, XIAO G Z. Stream Cipher and Its Applications[M]. National Defence Industry Press, 1994.

[19] KRASIKOV I, LITSYN S. On integral zeros of krawtchouk polynomials[J]. Journal of Combinatorial Theory, 1996, 74(1):71-99.

[20] FISCHER S, MEIER W. Algebraic immunity of S-boxes and augmented functions[A]. Advances in FSE 2007[C]. Berlin, Germany,2007. 366-381.