两种过程质量评价指标的西格玛水平转换

江 华

（中国航空工业空气动力研究院，辽宁 沈阳 110034）

在六西格玛管理中，很重要的一个内容是通过质量数据的计算分析结果，判定目前的过程、产品或服务的质量水平。评价质量水平涉及到的几个重要评价指标有：过程能力指数、百万机会缺陷数（DPMO）和西格玛水平（Z）等。过程能力指数是反映过程加工质量满足产品技术要求程度的评价指标；百万机会缺陷数也常用来综合度量过程质量；西格玛水平同样是描述过程质量满足规定要求能力的评价指标。作为过程质量评价指标，过程能力指数与西格玛水平、百万机会缺陷数（DPMO）与西格玛水平之间有着怎样的定量关系，过程能力指数、百万机会缺陷数又如何转换为西格玛水平，本文致力于这方面的研究。

1 西格玛水平（Z）

“西格玛”源于统计学中标准差σ的概念。标准差σ表示数据相对于平均值的分散程度，对于连续的可计量的质量特性，用σ来衡量其总体上对目标值的偏离程度。“西格玛水平”（即σ水平）则是将过程输出的平均值、标准差与顾客要求的目标值、规格限联系起来并进行比较。其中目标值是顾客要求的理想值；规格限是顾客允许的质量特性的波动范围。

1.1 过程无偏移的西格玛水平Z0

假定过程输出质量特性服从正态分布，并且过程输出质量特性的分布中心与目标值重合，即过程输出无偏移，西格玛水平Z0是指规格限与2σ的比值：

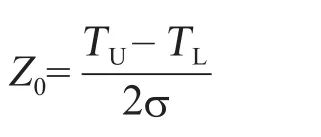
例如：某袋装绵白糖的平均重量是1 000ɡ，行业标准规定TL=982ɡ，TU=1 018ɡ，假定过程无偏移，当标准差σ=6ɡ时，西格玛水平为：

西格玛水平Z0=6时就是六西格玛管理追求的6σ质量目标，这时正态分布从-6σ到+6σ均在规范下限到规范上限范围内，过程输出的绝大多数都集中在顾客要求的目标值附近，过程满足顾客要求的能力很高。实现6σ质量目标需要持续改进过程质量，不断减小标准差。

1.2 生产中心漂移的西格玛水平

实际上，过程输出质量特性的分布中心与目标值完全重合的可能性很小，这种产品质量特性分布的均值μ与公差中心M不重合的现象称为生产中心的漂移。产品质量的变异由系统误差和随机误差叠加而成。

经验表明，在当前的科技水平下，生产过程稳定时中心漂移量能保持在1.5σ之内，漂移量过大时表明过程出现了异常变异，通过实施过程控制可以及时发现而重新调整到1.5σ之内，考虑到1.5σ的偏移，西格玛水平修正为：

例如：某送餐公司为某学校送午餐，学校希望在中午12:00送到，但实际总有误差，因而提出送餐时间限定在11:55分至12:05分之间，即TL为11:55分，TU为12:05分。过去一个星期来，该送餐公司将午餐送达的时间为：11:50，11:55，12:00，12:05，12:10。

这里，将送达时间按相对于目标值12:00的差值进行变换，记录为-10，-5，0，5，10，则平均送餐时间：假设本例的送餐时间服从正态分布，则样本标准差s为：

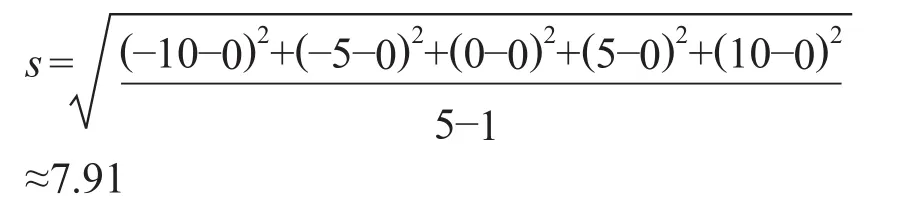
即该公司准时送餐的西格玛水平为2.13。

2 过程能力指数到西格玛水平的转换

2.1 过程能力指数

过程能力指数（Process Capability Index, Cp）反映了过程加工质量满足产品技术要求的程度，对于双侧公差情况，其计算公式为：

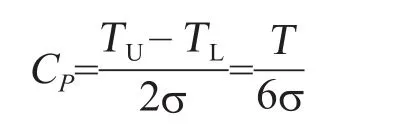
T为技术公差的幅度，即所允许的规格限，它反映了对产品的技术要求，而σ反映了过程加工质量的一致性。

当存在生产中心漂移时（如图1所示），修正后的过程能力指数为：

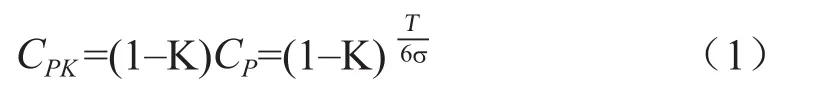
记分布中心µ对于公差中心M的偏移为ε=|M–µ|，则µ对于M的相对偏移（偏移度）K为：

例如：某种规格的轴，其直径要求为18±0.15 mm。长期检验结果表明，其直径服从X～N（18.06，0.042），则该规格轴生产的过程能力指数为：

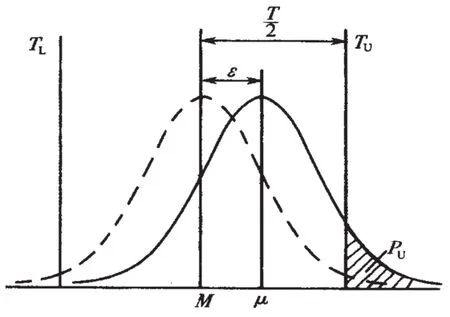
图1 产品质量分布的均值μ与公差中心M不重合的情况

采用控制手段，通过质量改进将生产中心漂移量控制为0.045 mm，标准差降为0.03，即当其直径服从X～N（18.045，0.032）时，则该规格轴生产的过程能力指数为：

2.2 过程能力指数到西格玛水平的转换

如上例中当某种规格轴直径服从X～N（18.06，0.042）分布，直径要求为18±0.15mm时，其过程能力指数为0.75，由已知可见存在生产中心漂移，且漂移量为ε=1.5σ，采用过程能力指数与西格玛水平转换公式，则该规格轴生产的西格玛水平为：

质量改进后，当该规格轴直径服从X～N（18.045，0.032）分布，直径要求不发生改变时，其过程能力指数为1.17，由已知得漂移量ε仍为1.5σ，则该规格轴生产的西格玛水平为：

可见西格玛水平的高低受到过程能力指数的影响，间接表现为受到与过程能力指数相关的生产中心漂移量和正态分布标准差的影响。在上下规格限一定、且稳定的生产过程分布中心与容差中心偏移量为1.5σ的情况下，正态分布的标准差越小（这时所允许的偏移量也小），过程能力指数越高，西格玛水平越高。因此，要提高西格玛水平就要提高技术能力（表现为标准差σ的减小）和技术管理能力（表现为减少偏移量）。

3 DPMO与西格玛水平的关系

3.1 用西格玛水平计算百万机会缺陷数（DPMO）

与不同西格玛水平对应是不同的不合格品率，下面我们来计算3σ水平下的不合格品率。由西格玛水平定义公式可计算3σ水平下T为6倍的标准差。

3.1.1 当质量特性X分布不存在偏移

设质量特性X服从正态分布N（µ，σ2），可知上规格限TU为µ+3σ，下规格限TL为µ–3σ，则产品质量特性X的不合格品率为：

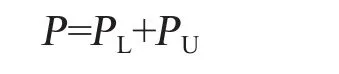
其中PL为X低于下规格限的概率，PU为X高于上规格限的概率，即：

3.1.2 当质量特性X分布存在偏移

设分布中心左偏移1.5σ，可知上规格限TU为µ+4.5σ，下规格限TL为µ–1.5σ，则产品特性X的不合格品率为P=PL+PU=Φ(–1.5)+[1–Φ(4.5)]=[1–Φ(1.5)]+[1–Φ(4.5)]=2–Φ(1.5)–Φ(4.5)，通过查标准正态分布函数Φ(x)表，得3σ水平对应的不合格品率为0.066 81，则每一百万个产品该质量特性的不合格数，即缺陷数为0.066 81×106=66 810。

可见，在3σ质量水平时，如果生产中心无漂移，DPMO=2700；如果生产中心有1.5σ漂移，DPMO=66 810。在过程稳定状态下，1.5σ是漂移量的上限，所以在3σ质量水平时实际的缺陷率是在0.27%～6.681%之间。在6σ质量水平时，如果生产中心无漂移，DPMO=0.002，几乎是零缺陷；如果生产中心有1.5σ漂移，DPMO=3.4。实际上，由于过程在长期运行中总会受到来自人、机、料、法、测、环（即5M1E）方面的影响，其输出质量特性的分布中心常常会向左或向右移动1.5σ，因此，通常所说的六西格玛质量水平对应的是3.4ppm缺陷率。

通过对不同西格玛水平的计算，我们可以求出在任何西格玛水平下的不合格品率，当用ppm单位表示不合格品率时，即可以求出每百万产品质量特性的缺陷数DPMO。

3.2 百万机会缺陷数DPMO到西格玛水平的转换

在3.1中我们反复提到的每一百万个某质量特性的缺陷数即为百万机会缺陷数（DPMO），它是六西格玛管理中常用的度量指标，其计算公式为：

如果我们统计了过程输出的缺陷数和缺陷机会数，利用上面公式就可以计算出百万机会缺陷数DPMO。例：某物料清单上有4个需要填表之处，均可能会发生填写错误，即该物料清单有4个缺陷机会。

在六西格玛管理中常常将DPMO折算为西格玛水平。DPMO对应于过程输出质量特性超出规格限的比率，可以通过对图2所示的正态分布中规格限外的部分求积分而获得。此时，标准正态分布中的分位数点Z，就是过程的西格玛水平。六西格玛管理中常用的西格玛水平值与DPMO换算的对应表见表1。

图2 缺陷率与过程输出西格玛水平的对应关系

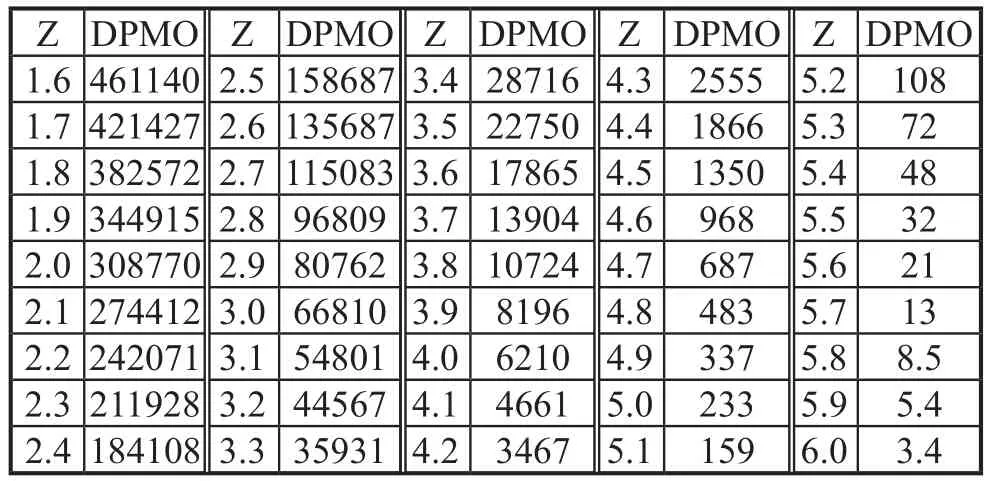
表1 西格玛水平值与DPMO对应表（考虑±1.5σ偏移时）

在应用中当我们求得了某质量特性的DPMO后，可通过查西格玛水平值与DPMO对应表获得该质量过程的西格玛水平，如上例中，查表可得该填写物料清单过程的西格玛水平为3.5（考虑到±1.5σ偏移）。通过给出西格玛水平值与DPMO二者之间的定量对应关系，解决了计算特性过程只能用合格率/不合格率来反映的问题。

4 结束语

建立过程能力指数与西格玛水平、百万机会缺陷数DPMO与西格玛水平的定量对应关系，在已知或通过计算得出其中一种评价指标的数值时，能很方便地通过换算获得生产过程质量特性的西格玛水平，便于各过程质量评价指标的同一平台比较，为质量管理工作者带来了方便，也为企业间的过程质量评价指标互信提供了基础。

[1] 全国质量专业技术人员职业资格考试办公室．质量专业理论与实务[M].北京：中国人事出版社，2011.

[2] 陶靖轩．六西格玛管理中的数据转换研究[J].统计与决策，2005（1）.

[3] 李平，张根保．西格玛水平与过程能力指数关系模型探讨[J]，现代制造工程，2007（2）.