格子-Boltzmann方法模拟霜结晶生长

龚建英 孙金绢 李国君

(西安交通大学能源与动力工程学院热流科学与工程教育部重点实验室 西安 710049)

格子-Boltzmann方法模拟霜结晶生长

龚建英 孙金绢 李国君

(西安交通大学能源与动力工程学院热流科学与工程教育部重点实验室 西安 710049)

为了研究冷壁面上霜结晶的生长过程以及各参数的变化规律，利用格子-Boltzmann方法(LBM)方法，建立一个二维介观模型，实验验证了模型的可靠性，分析了霜层温度变化和密度增长规律，并直观模拟出霜结晶凝聚变化过程。结果表明:霜层表面温度在早期阶段迅速增加，但增加率随着结霜时间增加而减小;霜层内部温度随霜层厚度的增加呈线性增长;霜层平均密度随结霜时间增加呈现出先慢后快的规律;随着结霜过程的进行，由于越往上，霜晶体积分数越小，导致霜层内部密度随霜层厚度的上升而减小。

格子-Boltzmann方法 冷壁面 霜结晶

1 引言

结霜现象的研究是涉及制冷、空调、航空、航天，农业等多领域中具有重要意义的一项基础性研究。霜的存在不仅降低系统的传热性能，增加压力损失，而且会导致除霜的能耗和运行成本的增加。因此，研究霜结晶生长的物理机制一直受到国内外学者的普遍关注。

近几十年中，结霜现象的研究方法主要分为数学模拟和实验方法。Lee等［1］把霜层看作多孔介质，提出了一个不同的理论模型。Sahin 发现霜的密度不仅仅是影响霜层有效导热系数的唯一参数。许多学者还通过实验方法研究了霜的形成过程，如，Tao等［3］用显微镜拍摄结霜过程，并把结霜过程分为3个阶段:结晶生长期，霜层生长期和霜层充分生长期。Kandula［4］用实验方法分析了冷壁面层流下霜的生长。虽然已经对霜层生长作了许多研究，霜结晶凝聚的物理机制和影响过程尚未完全明确，有必要采用更加先进有效的数学模拟方法结合实验，揭示霜结晶凝聚本质规律。

随着数值计算的快速发展，格子-Boltzmann方法(LBM)是近些年出现的一种新颖的数值计算方法，该方法基于分子动理论，具有清晰的物理背景，在宏观上是离散方法，微观上是连续方法，因而被称为介观模拟方法。该方法近些年来已成功地模拟流体流动和复杂结构的一个新工具［5］。与传统模拟方法相比，由于格子-Boltzmann方法对于复杂结构的适应性受到了广泛的关注，该方法在许多传统计算方法难以胜任的领域，如多孔介质、多相流等中取得了众多成功的应用［6］。

本文采用LBM对冷壁面霜晶生长过程进行数值模拟，并对模型的可靠性进行验证。从介观层面揭示了霜层表面温度和密度的变化规律，并阐明机理，直观模拟出霜晶体生长的二维变化图像，并对其进行深入分析。

2 格子-Boltzmann方法

格子-Boltzmann方法经过多年发展，很多模型被提出用以满足不同的应用要求。其中最基本最常用的模型，大致分为3部分:(1)等温模型;(2)非等温模型;(3)其它非标准模型。其中，本文中流场和温度场均采用了等温模型Bhatnagar-Gross-Krook(BGK)［7］近似法中的D2Q9模型。流体流动的格子-Boltzmann方程表达如下:

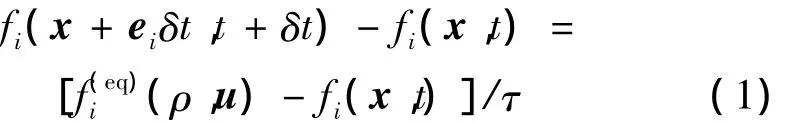
式中:fi是粒子速度分布函数，ei是离散速度，δt是时间步长，τ是无量纲松弛时间，与运动粘度v=cs2(τ-0.5)δt有关。平衡态分布函数定义为:

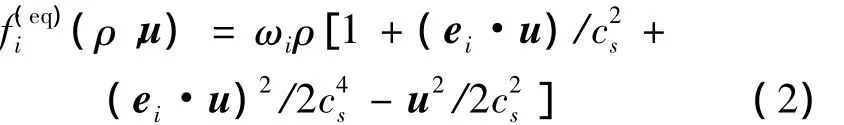
式中:声速cs=δx RT/δt，δx 是网格步长，RT=1/3。权系数分别为 ω0=4/9;当 i=1、2、3、4 时，ωi=1/9;当 i=5、6、7、8 时，ωi=1/36。离散速度 ei可以表达为:

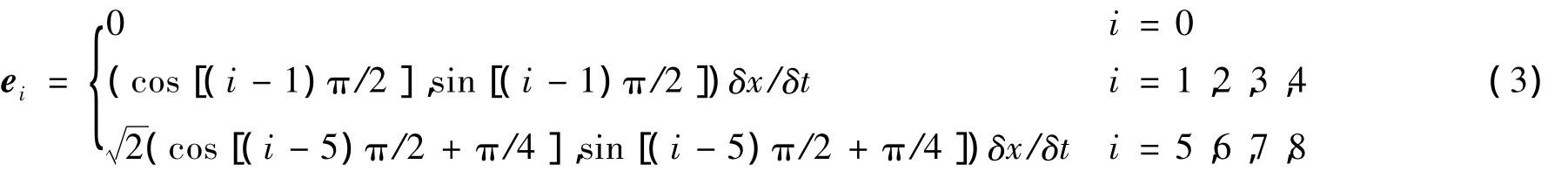
因此，模型的宏观密度和速度可以用以下方程计算:

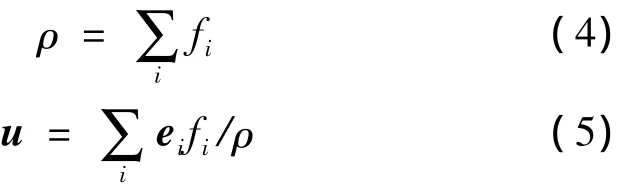
通过Chapman-Enskog展开方法，格子-Boltzmann方程可以推导出Navier-Stokes下的连续方程和动量方程［8］。

温度场中的演化方程如下所示:

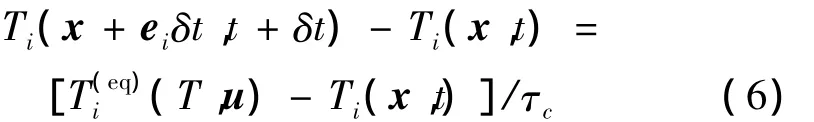
式中:Ti是温度分布态函数，τc是无量纲松弛时间。温度的平衡态函数T(eq)i表达如下:

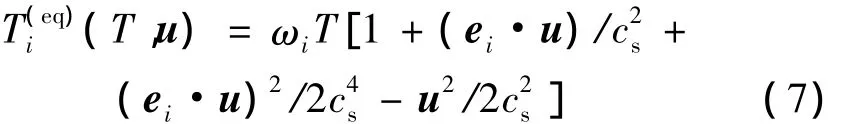
权系数ωi和等温声速cs与速度场中介绍的一样。模型的温度T定义如下:T=∑i

Ti(8)

通过Chapman-Enskog展开方法，格子-Boltzmann方程可以推导出本模型下对应的Navier-Stokes温度宏观方程［9］。

格子-Boltzmann方程的演化过程比较清晰，主要包括迁移和碰撞两个过程，迁移和碰撞是两个相对独立的粒子运动过程。

粒子迁移:

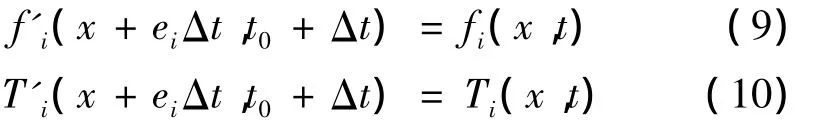
粒子碰撞:

3 边界条件

LBM中，边界条件通过分布函数获得。空气来流速度保持为恒定的初始速度，空气上方、出流的格点速度与冷壁面格点速度均为0，空气上方、来流和出流的格点温度保持恒定湿空气温度，而冷壁面格点温度保持与冷板温度一致。对于冷壁面格点和固体格点均采用无滑移边界条件中的反弹格式［7］，即当粒子到达格点后被原路返回到流体内部，且运动方向和入射方向相反。符合准静态假设，虽然边界只提供了一阶精度，但是该方法需要较少的计算时间，能有效地处理复杂结构的无滑移条件。如图1a所示，边界格点(i，1)的未知分布函数可由式(13)获得，即:

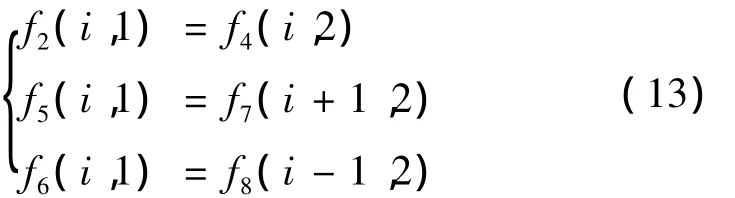
除了以上格点采用反弹格式，其余格点均采用了非平衡态外推格式［7］，这种格式数值稳定性好，计算量小并且适用范围广泛。边界格点上的分布函数主要分为平衡态和非平衡态两部分，其中平衡态部分是由一个新构造的平衡态分布来近似，非平衡态部分是由一个一阶精度的外推方法来获得。如图1b所示，格点EOA位于边界上，格点BCD位于流场内，格点FGH位于流场外。边界格点O的未知分布函数f2，5，6(xO，t)，可由式(14)获得，即:

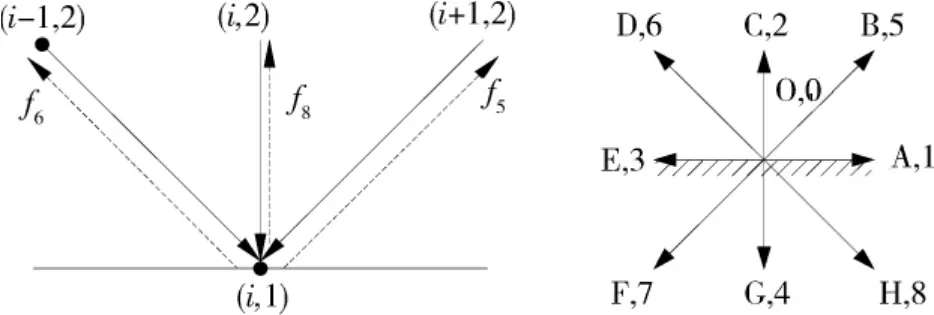
图1 边界格式Fig.1 Boundary scheme

4 模拟结果和讨论

运用LB模型模拟介观尺度下冷壁面上霜结晶生长过程及其各参数变化规律。采用的几何结构被划分为800×400的二维网格。首先，给定各个物理变量的初始值，如空气的湿度、速度、温度、密度，冷壁面温度，松弛时间，晶格大小，以及边界条件等。在网格底部，分布有一定数量的随机晶核。晶核的数量由霜晶体初始体积分数决定。根据方程(2)和方程(7)，求出流场和温度场初始的平衡态分布函数。初始的粒子速度分布函数为fi(x，t0)=feqi(x，t0)，温度分布函数为Ti(x，t0)=Teqi(x，t0)。然后，通过成核理论［10］求得霜晶体质量增加，并得到霜晶体新一步的体积分数。而格点随着霜晶体体积分数增加，由流体相变为固体相。最后，由式(1)—式(8)结合边界条件，求得流场和温度场的分布函数和湿空气在每一个格点上的密度、速度和温度的分布。

图2是霜层表面温度随霜结晶生长的变化曲线。圆圈代表Lee的实验数据，线代表模型计算出的结果。从图中可以看出，模拟的结果与文献中的实验数据的变化趋势是比较一致的，证明了模型的可靠性。

图2 霜表面温度随时间的变化Fig.2 Effect of frost time on frost surface temperature

霜层表面温度是一个重要的参数，对通过水分子凝聚在冷壁面造成的霜晶体的密度变化及形态影响很大，由图2可知，在霜晶体生长初期阶段，霜表面温度变化迅速，但是随着时间的推移，温度的变化速率变得缓慢，并不断趋近于三相点温度。

图3是在矩形域内霜结晶生长二维几何结构的温度分布图。图中纵坐标代表的霜晶体纵向生长的高度，横坐标表示的是霜晶体的横向生长。从图中可以直观地观察到晶体的凝聚与温度随结霜时间的变化过程，底部靠近冷壁面的位置，霜晶温度较低，越往上温度越高，而由于周围环境中温度较高的湿空气向内扩散，冰晶空隙处温度较高。图4显示了不同时刻霜层内温度随厚度的变化曲线，从图中可以看出在任一结霜时刻，霜层内部温度随霜层厚度增大几乎都呈线性增长。在相同霜层厚度处，随时间的推移温度不断降低，但变化幅度很小。

图3 霜结晶凝聚直观图Fig.3 Simulated temperature field at different times

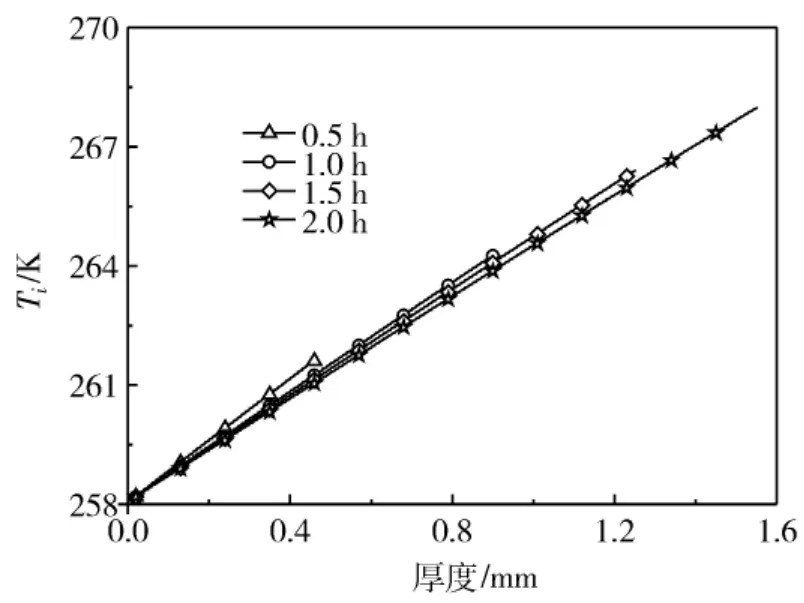
图4 霜内部温度不同时刻随霜层厚度的变化Fig.4 Effect of frost thickness on frost internal temperatures

图5给出了霜的平均密度随结霜时间的变化曲线。由图可见:霜的密度随时间在不断增加。在结晶初期，由于霜晶呈现较强的枝状生长，表现在霜层厚度的增加，而密度增长较慢，所以初期曲线呈凹形。随着霜结晶的进行，湿空气分子不断扩散和凝华，使密度后期不断增大，所以后期曲线斜率较大，即增长速率较大。除此之外，霜内部密度还随着霜层的厚度而变化，如图6所示。从图中可以看出，同一时刻，随着霜层厚度的增加，霜层密度在降低，这是由于越往上，霜晶体积分数越小，而密度越接近空气密度;在相同霜层同一厚度处，随着时间的增加，密度越来越大，原因在于水蒸气分子不断沉积凝聚到霜晶体中，导致密度不断增大。

图5 霜的平均密度随时间的变化Fig.5 Effect of frost time on frost average density

5 结论

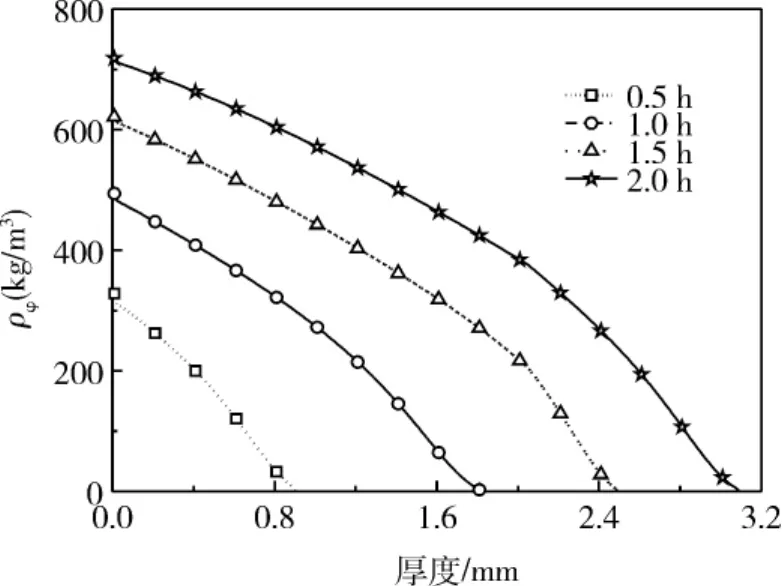
图6 霜内部密度不同时刻随霜层厚度的变化Fig.6 Effect of frost internal density onfrost layer thickness

建立了与传统方法不同的格子-Boltzmann模型成功模拟霜表面温度和密度随霜结晶生长的变化过程。模拟结果与文献中的实验数据较为吻合，得出以下主要结论:

(1)霜层表面温度在早期阶段迅速增加，但增加率减小。此外，内部温度随霜层厚度的上升呈线性曲线。

(2)直观模拟出晶体的凝聚与温度随结霜时间的变化过程，霜层靠近冷壁面的位置，霜晶温度较低，沿冷壁面法线方向越往上霜层温度越高。

(3)霜层平均密度随结霜时间增加呈现出先慢后快的规律;霜层内部密度随霜层厚度的上升而减小，原因在于随着结霜过程的进行，越往上，霜晶体积分数越小，导致密度减小。

1 Lee K S，Kim W S，Lee T H.A one-dimensional model for frost formation on a cold flat surface［J］.International Journal of Heat and Mass Transfer，1997，40(18):4359-4365.

2 Sahin A Z.Effective thermal conductivity of frost during the crystal growth period［J］.International Journal of Heat and Mass Transfer，2000，43(4):539-553.

3 Tao Y X，Besant R W，Rezkallah K S.A mathematical model for predicting the densification and growth of frost on a flat plate［J］.International Journal of Heat and Mass Transfer，1993，36(2):356-363.

4 Kandula M.Frost growth and densification on a flat surface in laminar flow with variable humidity［J］.International Communications in Heat and Mass Transfer，2012，39(8):1030-1034.

5 Pan Chongxun，Luo Li-Shi，Miller C T.An evaluation of lattice Boltzmann schemes for porous medium flow simulation［J］.Computers ＆Fluids，2006，35(8-9):898-909.

6 Guo Zhaoli，Zhao T S.A lattice Boltzmann model for convection heat transfer in porous media［J］.Numerical Heat Transfer，Part B:Fundamentals:An International Journal of Computation and Methodology，2005，47(2):157-177.

7 郭照立，郑楚光.格子Boltzmann方法的原理及应用［M］.北京:科学出版社，2009.

8 Hou Shuling，Zou Qisu，Chen Shiyi，et al.Simulation of cavity flow by the lattice Boltzmann method［J］.Journal of Computational Physics，1995，118(2):329-347.

9 Ergun S.Fluid flow through packed columns［J］.Chemical Engineering Progress，1952，48(2):89-94.

10 Becker R，Doring.W The kinetic treatment of nuclear formation in supersaturated vapors［J］.Annals of Physics-Leipzig，1935，24:719.

Frost crystal growth simulation by lattice Boltzmann method

Gong Jianying Sun Jinjuan Li Guojun

(MOE Key Laboratory of Thermo-Fluid Science and Engineering，School of Energy and Power Engineering，Xi’an Jiaotong University，Xi’an 710049，China)

In order to calculate the frost crystal growth process on a cold flat surface and study the variation laws of parameters，a two-dimensional mesoscopic model was proposed based on LBM.The predicted results were found to be in good agreement with the data reported in the literatures.This simulation was concerned with temperature and density variation of the frost.The results show that the surface temperature increases rapidly in the early-stage，but the increase rate decreases with frosting.In addition，the interior temperatures rise in a linear curve with increase of the frost layer thickness.The average frost layer density increases with increasing frosting time.It was also found that the nearer the frost layer gets to the cold flat surfaces the higher the frost density is.

lattice Boltzmann method;frost crystal growth;cold flat surfaces

2013-03-07;

2013-06-14

国家自然科学基金项目(51106013、50806059)、中国博士后科学基金(2012M511998)。

龚建英，女，36岁，博士、讲师。

TB611、TK121

A文章编号:1000-6516(2013)04-0010-04