热沉调温系统中的热学模型分析

王紫娟 丁文静 刘 然 付春雨

(北京卫星环境工程研究所 北京 100094)

热沉调温系统中的热学模型分析

王紫娟 丁文静 刘 然 付春雨

(北京卫星环境工程研究所 北京 100094)

通过分析热沉调温系统中热沉、载冷剂、试件间的热量传递关系，在工程应用允许的范围内，基于一定的假设，对热沉与载冷剂、热沉与试件以及试件本身3部分分别进行了热学模型的建模分析，并将以上3个模型通过模糊PID控制算法进行关联，仿真模拟了载冷剂先通过对流换热控制热沉温度，热沉再通过辐射换热来控制试件温度的整个调温过程。结果显示调温过程初期试件温度迅速降低;接近目标温度后，载冷剂温度升高带动热沉温度升高，从而减小试件温度降温速度;系统稳定到目标温度设定偏差范围内后，试件温度收敛，热沉与载冷剂温度维持恒定状态。

调温系统 模型 热沉 控制框图

1 引言

冷黑空间环境是航天器在飞行轨道中经历的主要环境之一，模拟空间冷黑环境的热沉是航天器热试验的3个基本条件之一［1］。目前对于热沉的研究重点多集中于制冷剂与不同结构热沉间的换热性能上，如姜传胜分析了不同热沉片结构对支管流量分配的影响［2］，于涛对影响管板式热沉热均匀性的因素进行了研究［3］，袁修干改进了管板式热沉温度均匀性的理论计算和工程设计方法［4］，张磊通过建立不锈钢板式热沉的几何结构模型，用流体力学理论和有限元方法对热沉换热性能进行数值计算，探讨流速和进出液口布置形式对板式热沉强化传热的效果［5］。

热沉调温系统是指利用外部温度控制设备，通过向热沉中通入温度和流量可控的介质，将热沉温度控制在规定的温度范围内，从而利用热沉温度的改变来实现试件温度的升高、降低以及试件温度控制的温度控制系统。该方法在真空热试验中，不需要配置真空环境下的电加热装置对试件进行加热或温度控制。

由于试验的目的不同，热沉调温系统配置往往差别很大，可根据试验的温度范围采取不同的途径去实现，温度循环流程不同使得热真空试验设备也会有很大差别，而且在做试验过程中因设备的温度循环流程不同而带来操作的难易差别也很大。

空间电子产品真空热试验的温度范围一般为-40℃至+60℃，对应的热沉温度范围一般为-70℃至+80℃。-80℃至+150℃温区的热真空试验，通常有低温酒精与红外加热配合的调温流程、气氮调温流程以及宽量程导热油调温流程3种热沉温度调控系统。其中导热油在较宽温区内(-80℃至+150℃)都是液体状态，试验操作方便，同时导热油具有较大的热容量，温度滞后小，可更加真实的模拟试件的温度变化。所以，以导热油为载冷剂的热沉调温系统可满足一般电子产品热真空试验的需求，本文将对以导热油为载冷剂的热沉调温系统热学模型进行分析研究。

2 热学模型建模

热学模型建立需进行如下假设:

(1)工作介质为不可压缩的牛顿流体;

(2)流体重力和由于密度差引起的浮升力忽略不计;

(3)热沉板与载冷剂的辐射换热忽略不计;

(4)载冷剂在热沉内强制流动且流速较低，忽略载冷剂流动时因粘性耗散产生的热效应;

(5)载冷剂在热沉内均匀流动。

2.1 热沉-载冷剂(导热油)换热数学模型

热沉采用不锈钢材料的板式热沉，为建模的方便，取单位面积热沉进行分析。热沉内表面为与载冷剂的对流换热，考虑到载冷剂物性参数沿长度方向的变化，将热沉划分为n个节点，取长度为dl的微元体作为控制体(图1)。

对流换热问题的完整数学描述包括连续性方程、动量守恒方程和能量守恒方程。

连续性方程:

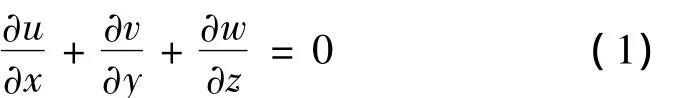
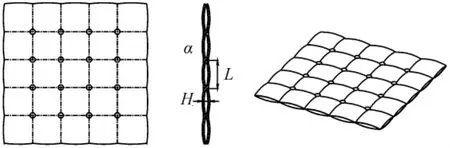
图1 不锈钢板式热沉结构示意图Fig.1 Structural diagram of the plate heat sink

式中:u、v、w 为速度矢量在 x、y、z方向上的分量。

i方向直角坐标系中的动量守恒方程:

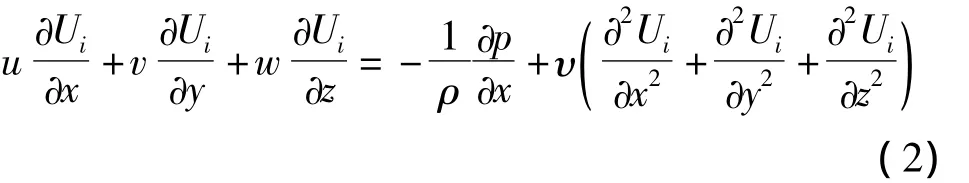
式中:ρ为流体密度，p为压力，υ为运动粘度，Ui为i方向的速度分量。

能量守恒方程:

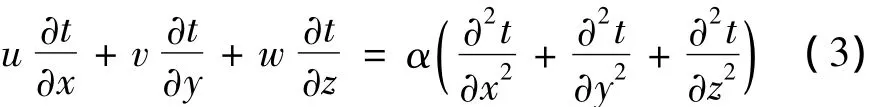
式中:α为热扩散系数，t为流体温度。

当使用上述控制方程描述湍流流动时，u、p、t等均为瞬时值。采用RNG模型的k-ε方程对湍流进行模拟［6］:

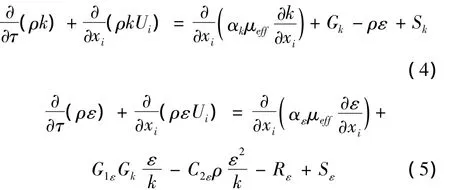
式中:Gk为由平均速度而产生的湍流动能;G1ε、G2ε为模型常量，分别为 1.42 和 1.68;αk、αε为 k 方程和ε方程的湍流Prandtl数;Sk、Sε根据具体条件进行定义。

其中对于层流:Nuf=4.364，对于湍流和过渡流:采用格尼林斯基(Gnielinski)公式［7］:

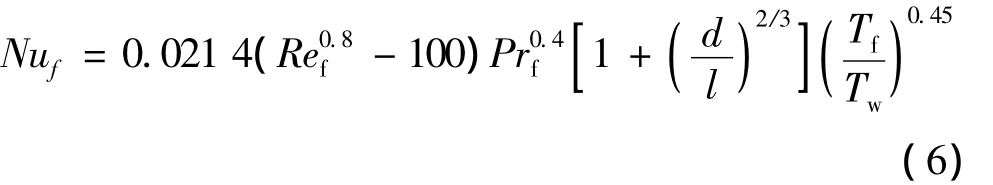
式中:Tf、Tw为流体、壁面平均温度。

2.2 试件换热数学模型

对试件的处理可简化为两种情况进行分析:一种试件为金属等导热系数大的材料，其在与外界换热过程中，内部温度场均匀，可以将其内部导热热阻忽略，即采用集总参数法。

由集总参数法能量守恒方程:

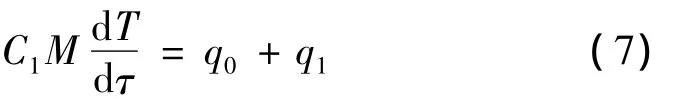
式中:C1为试件比热容;M为试件质量;q0为试件内热源;q1试件与热沉辐射换热量。

对于不能利用集总参数法的试件，如一些内部热阻较大的非金属材料，可以将试件简化为和实际试件相同材质、质量、外表面积的实心圆柱体，从而便于按一维导热处理问题。如图2所示，将试件结构分成m层。

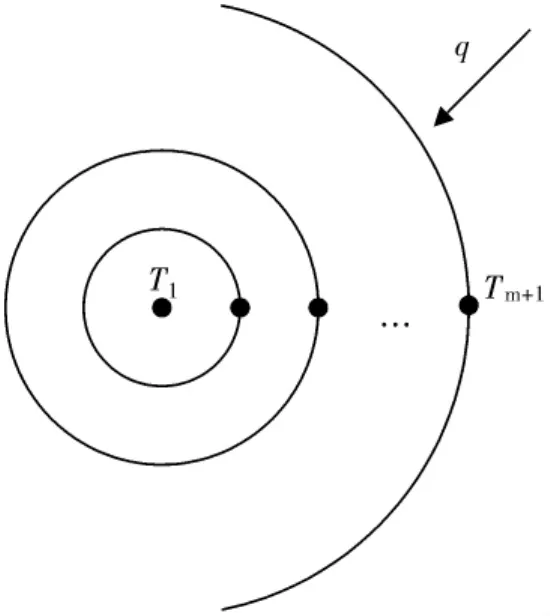
图2 试件换热模型Fig.2 Heat transfer model of specimen

对于圆柱形物体的一维导热有:

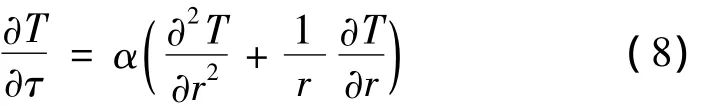
式(8)右边按二阶精度离散化后为:

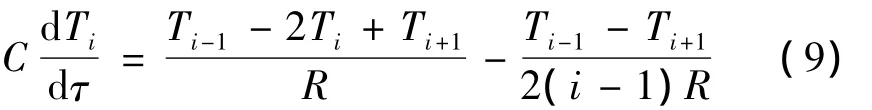
式中:C为试件的单位比热容，C=Δrρcp，R 为热阻，R=Δr/λ。

对于核心点，该点控制体内能的变化等于由它向第二个控制体导出的热量，有:

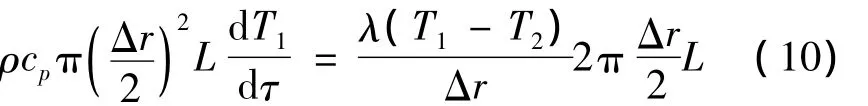
式中:L为试件简化后圆柱体长度。

则试件各个节点的换热方程如下:

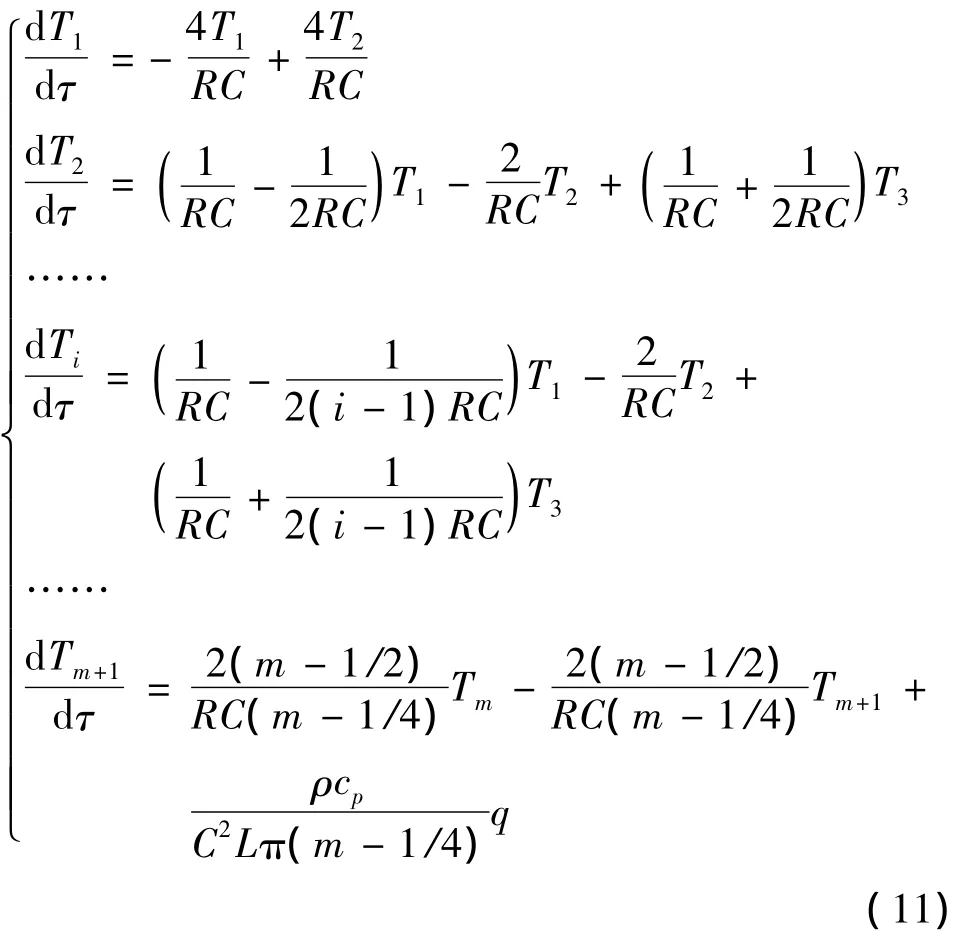
2.3 热沉与试件间的辐射换热模型

热沉与容器壁以及热沉与试件的辐射换热可以看成是辐射换热的基本类型:两等温表面的灰体辐射换热。两表面的辐射换热公式［8］:

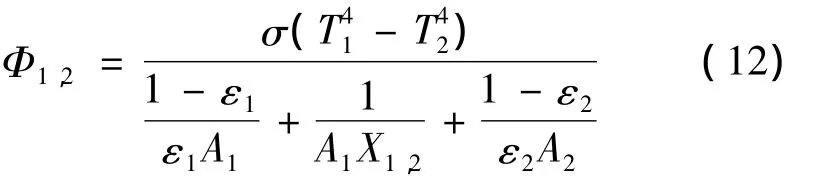
式中:T1、T2为两物体的温度，σ=5.67×10-8W/(m2·K4)为斯忒藩 -玻耳兹曼常量，ε1、ε2为两物体表面发射率，A1、A2为辐射表面积，X1，2为表面1对表面2的角系数。

3 调温过程模拟及分析

以采用宽量程导热油进行热沉温度调控的热沉调温系统为例，进行调温过程分析。导热油在-80℃到+150℃温区范围内为液体状态，导热油在热沉管内流动，通过对流与传导来调控热沉温度，当热沉降温时，制冷机组开启，通过板换来冷却导热油，导热油通过循环泵来冷却热沉;当热沉升温时，则有电加热器提供热源，加热后的导热油通过循环泵给热沉升温。通过以上流程分析可以看出，通过确定进入热沉的导热油的温度和流量，就可以对热沉的温度实现精确调控。

3.1 热沉调温系统

热沉调温系统如图3所示，主要包括制冷机组、电加热器、循环泵、冷却器、导热油缓冲容器、热沉及温度压力测点等设备。

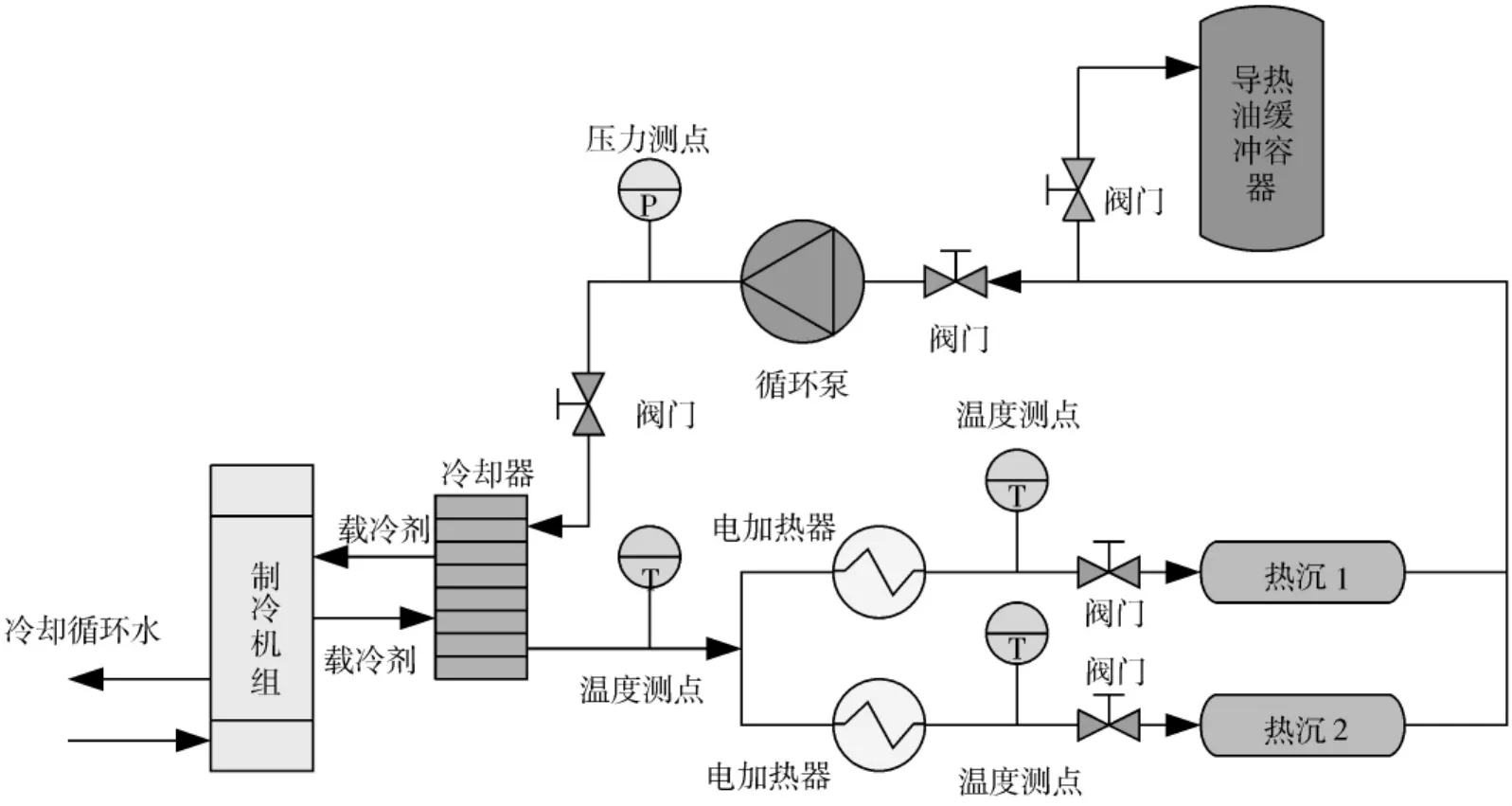
图3 调温系统图Fig.3 Thermal regulating system diagram

3.2 调温过程分析

调温系统采用导热油为载冷剂，主要由导热油温度控制设备(制冷机组和电加热器)、配套管路及相应的阀门、传感器组成，系统中的压力传感器，传感器状态信号通过模拟量输入模块接入PLC中。

开度阀门通过PLC的模拟量输出控制，开关阀通过PLC的数字量输出模块控制。

导热油调温方式中采用改变导热油温度从而使热沉温度改变的手段，来达到控制试件温度的目的。控制过程分为两个闭环负反馈系统:其一为通过调节导热油温度来调节热沉温度的闭环系统(简称热沉闭环);其二为通过调节热沉温度来调节试件温度的闭环系统(简称试件闭环)。这两个闭环系统之间是串联的关系。

热沉闭环控制算法为模糊PID控制的控制方式，即通过调整电加热器提供给导热油的加热功率，从而改变进入热沉的导热油温度的，以达到调整热沉温度的目的。由于控温仪输出通用模拟信号0—10 V或4—20 mA，热沉闭环中配置1台控温仪控制热沉温度。控制结构框图如图4所示。

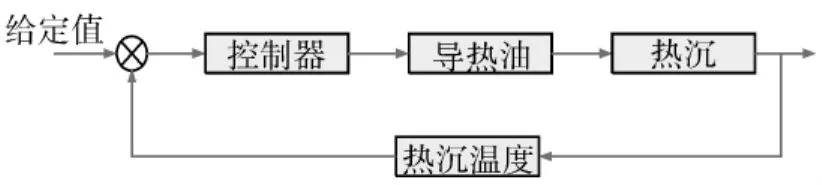
图4 热沉温度控制框图Fig.4 Shroud temperature control block diagram

试件闭环控制算法为二级模糊PID控制的控制方式，即通过调整电加热器提供给导热油的加热功率或调整进入热沉的导热油流量，从而改变热沉温度，以达到调整试件温度的目的。其控制框图如图5所示。该控制算法在上位组态软件中实现。

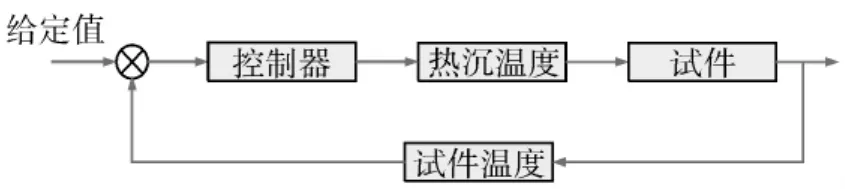
图5 试件温度控制框图Fig.5 Specimen temperature control block diagram

3.3 热沉调温仿真计算

热沉调温系统仿真如图6所示。由仿真结果可以看出，试件温度在调温初期下降较快，但当试件温度接近目标温度时，为防止温度超调过大，控制参数进行整定，升高载冷剂温度，从而提升热沉温度使得试件温度下降速度降低。当系统稳定后，由于稳态误差的存在，试件温度与目标温度有一定偏差，但在允许范围之内。仿真结果同时显示了载冷剂的温度变化:调温刚开始时温度变化不大，当试件温度接近目标温度时有明显升温，调温后期载冷剂温度基本保持稳定。由于试件温度曲线是收敛的，在实际操作中，可以设定当偏差在一定范围内时，载冷剂温度保持不变。

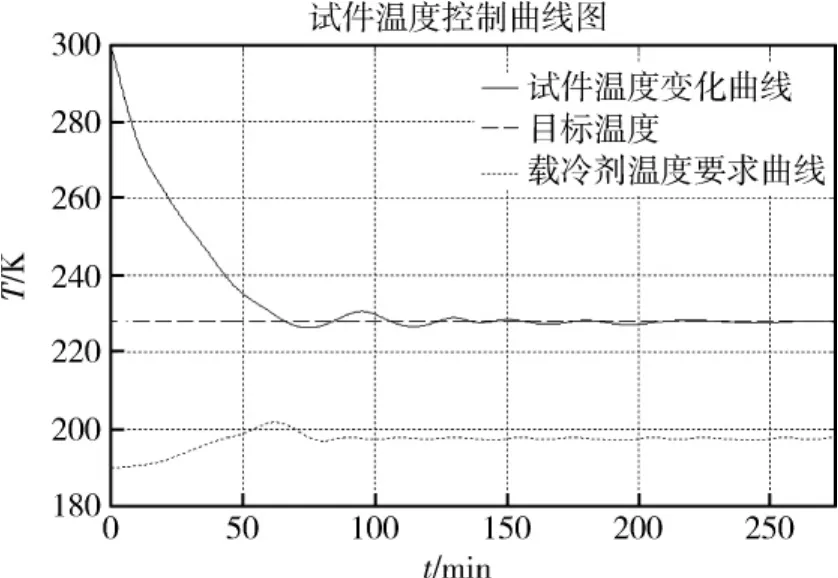
图6 模型仿真结果Fig.6 Model simulation result

4 结论

热沉调温系统是通过载冷剂温度、流量的变化来控制试件的温度，使试件达到试验要求的目标温度值。本文通过对热沉与载冷剂、热沉与试件以及试件本身进行建模分析，并通过控制算法将以上热学模型进行关联，得到了载冷剂与热沉、热沉与试件以及试件自身间的热量传递计算模型，模拟分析了采用载冷剂系统进行热沉调温的整个过程，为此类系统热沉调温技术及控温软件的开发奠定了基础。

1 王浚，黄本诚，万才大.环境模拟技术［M］.北京:国防工业出版社，1996:490.

2 姜传胜，王浚.大型空间环模器热沉热设计研究［J］.北京航空航天大学学报，2001，27(3):305-308.

3 于涛，刘敏，邹定忠.航天器空间环境模拟器热沉热均匀性分析［J］.中国空间科学技术，2006(6):37-41.

4 袁修干，刘国青，刘敏，等.大型液氮热沉中流动与传热均匀性数学模拟与分析［J］.低温工程，2008(2):18-21.

5 张磊，刘敏，刘波涛.流速及进出液口形式对板式热沉换热性能影响［J］.航天器环境工程，2012(5):98-102.

6 Yakhot V，Orzag S A.Renormalization group analysis of turbulence:basic theory［J］.Journal of Scientific Computing，1996(1):3-11.

7 陶文铨.数值传热学(第二版)［M］.西安:西安交通大学出版社，2001.5.

8 杨世铭，陶文铨.传热学［M］.北京:高等教育出版社，1998:134.

Numerical model analysis on thermal regulating system

Wang Zijuan Ding Wenjing Liu Ran Fu Chunyu

(Beijing Institute of Spacecraft Environment Engineering，Beijing 100094，China)

The heat models of shroud and refrigerating fluid，shroud and specimen，and specimen itself were established based on some hypothesis to analyze the heat transfer relationship among the shroud，refrigerating fluid and the specimen.Three models were related by PID control theory and used to simulate the whole temperature regulating procedure of the specimen.The results show that at the beginning，the temperature of the specimen drops rapidly to the target temperature，and then the temperature of the shroud increases with the temperature increasing of refrigerating fluid to slow down the cooling velocity of the specimen.When the system stabilizes in the range of the designed error，the temperature of the specimen converges and the temperature of the shroud and refrigerating fluid keeps stable.

thermal regulating system;model;shroud;control block diagram

TB611、V416.5

A

1000-6516(2013)04-0041-04

2013-05-09;

2013-06-27

王紫娟，女，36岁，高级工程师。