带挠性伸杆机构小卫星的复合振动控制*

任善永 楚中毅

(北京航空航天大学惯性技术重点实验室新型惯性仪表与导航系统技术国防重点学科实验室，北京 100191)

带挠性伸杆机构小卫星的复合振动控制*

任善永†楚中毅

(北京航空航天大学惯性技术重点实验室新型惯性仪表与导航系统技术国防重点学科实验室，北京 100191)

为了满足空间探测任务的要求，需采用轻质的伸杆机构支撑各类探测载荷远离卫星本体以避免平台剩磁对空间测量信息的干扰，而挠性伸杆的弹性振动会耦合影响到卫星本体，从而降低卫星本体的姿态控制精度．考虑到挠性附件振动的复杂性及其对航天器本体的耦合影响，采用最优指令整形抑制挠性伸杆的低阶模态振动，并在本体控制中设计自适应扰动抑制滤波器进一步抵消挠性伸杆的残余振动对本体的干扰作用．仿真结果表明，此复合振动控制方法可显著的提高此小卫星的姿态控制精度．

挠性伸杆， 最优指令整形， 自适应扰动抑制滤波器， 复合振动控制

引言

近年来小卫星以成本低、质量轻、体积小、易发射、研制周期短等优点，使其在侦查、导航、测绘等领域得到了广泛的应用．然而，日－地空间环境(特别是地球空间磁场模式)会影响到各种空间任务的工作特性，甚至会降低航天器的可靠性，所以对日－地空间环境的探测工作是非常必要的．与此同时，为了满足探测任务的性能要求，避免卫星台本身的剩磁对空间信息的干扰，须采用伸杆机构支撑各类探测载荷或传感器使其远离卫星本体，从而保证探测数据的准确性和空间信息的精确度．受运载空间、运载能力和能源消耗的限制，往往将伸杆做成轻质、可伸缩或可折叠的结构，所以伸杆具有一定的挠性特性．挠性伸杆的弹性振动不可避免地会耦合影响到小卫星本体，导致卫星本体的振动，从而影响小卫星的姿态控制精度和稳定度．因此如何有效地抑制挠性伸杆的振动及其对卫星本体的耦合影响是提高此类小卫星姿态控制精度的关键问题之一．

国内外对挠性航天器的振动控制问题进行了大量的研究，主要有鲁棒控制［1］、变结构控制［2］、指令整形［3，4］等控制方法．鲁棒控制方法将稳定性和可靠性作为首要目标，要求过程的动态特性已知，且不确定因素的变化范围可以预估，不需要精确的模型，但鲁棒控制器的阶数往往偏高，限制了其在航天领域的应用．变结构控制器采用任意快速开关强迫系统变量沿优化的相空间轨迹滑动，其鲁棒性较好，但会带来输出抖动的问题．指令整形是一种简单的前馈控制方法，非常适合用来抑制挠性结构的残余振动．他将脉冲序列与一定的期望输入相卷积，所形成的指令作为输入来控制系统运动，其中脉冲序列与系统的振动频率以及阻尼有关，在工程中已经得到广泛的应用［5］．但它的一个缺点就是会引入时滞，特别是当需要抑制多阶模态振动时，仅采用此方法会引入相当长的时滞．考虑到弹性振动通常具有周期性的特点，可考虑在反馈控制系统中引入滤波器来抵消振动干扰的影响，且此方法易于工程实现．本论文针对上述问题对带挠性伸杆小卫星的振动控制方法进行了研究．

1 动力学模型

现只考虑卫星本体的单轴机动以及挠性伸杆在其坐标系平面内绕关节的转动和杆的弯曲变形，忽略其平面外的耦合影响，则此挠性小卫星可简化为图1所示模型

如图所示，卫星由刚性本体、挠性伸杆一和杆二构成．OXY为轨道坐标系，o0x0y0为航天器本体坐标系，oixiyi(i=1，2)为附件坐标系．θ0为本体相对于惯性轴的转角，θ1，θ2分别为杆与本体坐标系中o0x0轴的夹角，u1，u2为杆的弹性形变．

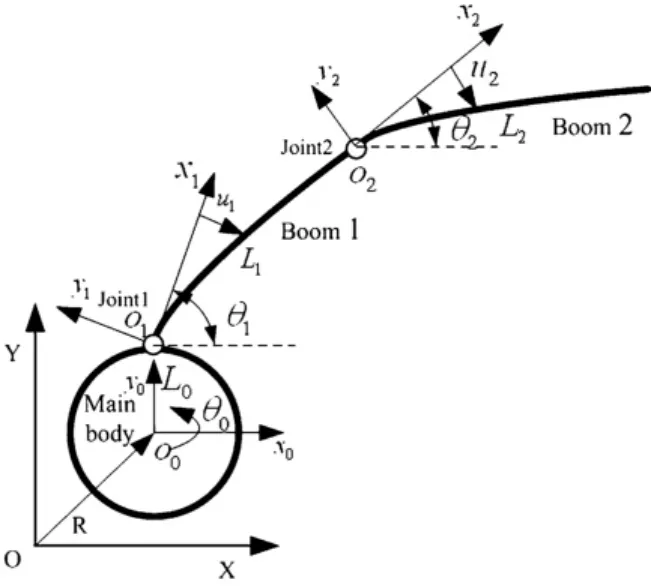
图1 带挠性伸杆的航天器模型Fig．1 Model of spacecraft with flexible booms

若只考虑挠性杆的横向振动，忽略轴向以及剪切变形，则挠性伸杆可视为Euler－Bernoulli梁．弹性形变u1，u2可由假设模态法表示为

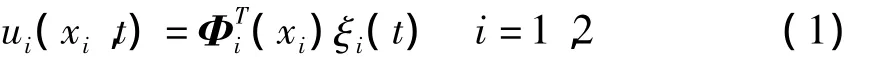
式中Φi(xi)为模态振型函数，ξi(t)为振型的广义坐标．

现定义广义坐标向量q=［xyθ0θ1θ21］，则整个系统的动能和势能可以表示为

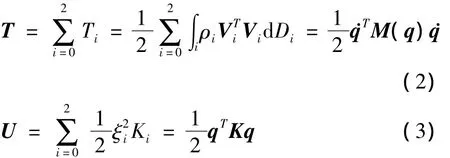
定义拉格朗日函数为

对拉格朗日函数求微分得

将式(2)、(3)、(4)代入式(5)中，得到矩阵形式的动力学方程

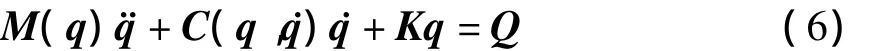
式中，M(q)、C(q，q)、K和Q分别是系统的广义质量矩阵、阻尼矩阵、刚度矩阵和广义力［6］．

2 控制器设计

系统的控制框图如图2所示，挠性伸杆的控制中采用最优指令整形器抑制其结构振动，同时在卫星本体控制中采用自适应扰动抑制滤波器来进一步减小挠性伸杆的残余振动对本体姿态控制的耦合影响．

图2 系统的控制框图Fig．2 Structure of control system

2．1 基于最优指令整形器的挠性伸杆振动控制

模型中的挠性伸杆是振动的源头，要想从整体上提高卫星的姿态控制精度就必须对其进行振动抑制，本文采用指令整形技术对其结构振动进行抑制．

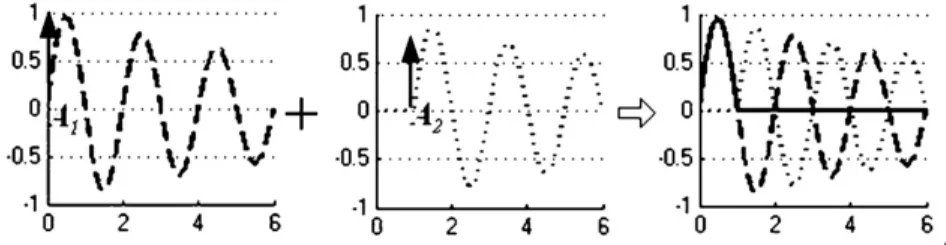
图3 指令整形技术的原理Fig．3 Theory of input shaping technology

如图3所示，将两个不同幅值的脉冲信号适时地作用到一系统，则脉冲A1δ(t－t1)引起的系统响应与脉冲A2δ(t－t2)引起的系统响应叠加后就可以使时刻后的系统响应为零．

常规指令整形器的延迟时间是系统半振动周期的整数倍，受振动频率制约，为了提高系统的相应速度，降低引入系统的时滞，通常选用时间最优指令整形器，设二阶系统的状态方程为

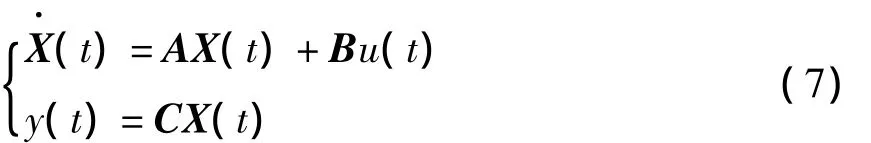
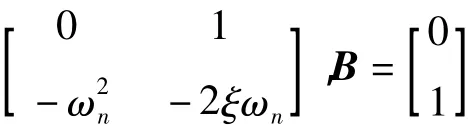
假设系统是线性的，且初始状态为零，以上状态方程的解可用状态转移矩阵Ψ(t，τ)表示

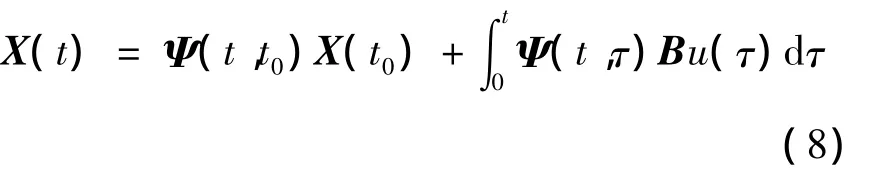
为了设计时间最优的指令整形器，选取二次型目标函数［7］

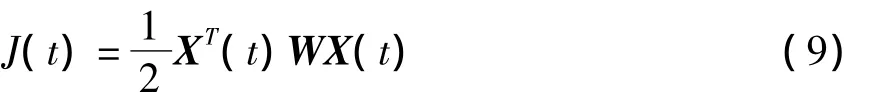
式中，W为二阶单位正定加权阵．

设指令整形器的传递函数为

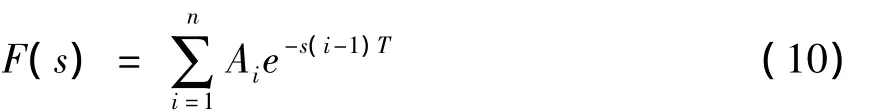
则其单位脉冲响应为

取n=3，A1=1，X(0)=0，则目标函数可简化为

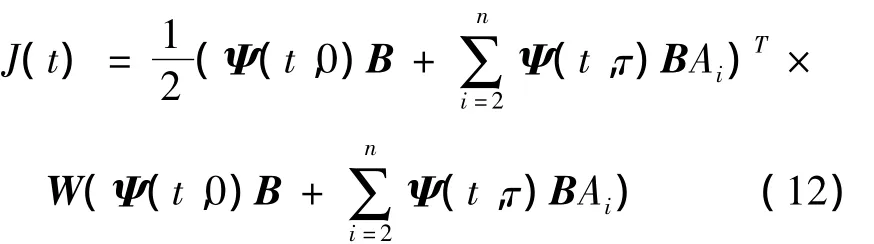
令 Φ(t)=［Ψ(t，T)BΨ(t，2T)B］，f=［A2A3］T，则式(12)可简化为

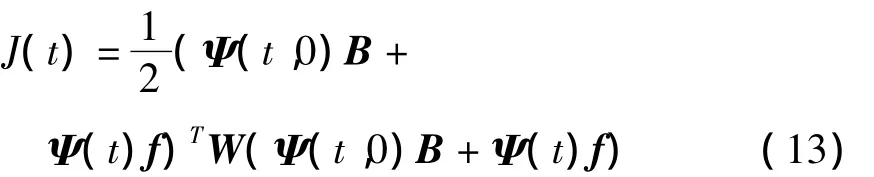
根据优化理论，目标函数最小的充要条件为

求解方程(14)、(15)，得

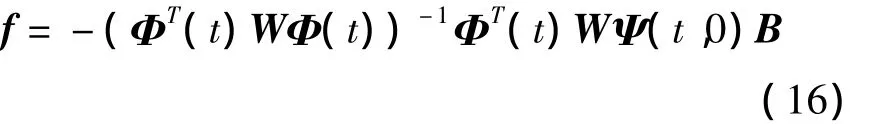
将状态转移矩阵代入式(16)，并进行归一化处理，可得

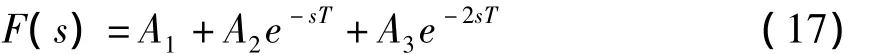
其中，脉冲的幅值为

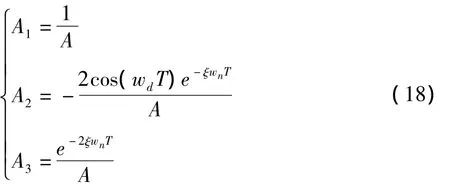
式中，带阻尼固有频率延迟时间从理论上讲是可以任意设定的，但实际中要根据振动抑制的效果和响应速度而合理的选取，最优指令整形引入系统的时滞为2T．

为避免对系统引入较长的时滞，本文采用的最优指令整形只对挠性伸杆的一阶模态振动进行抑制，并配合使用简单的PD反馈控制以降低控制算法的复杂性．

2．2 基于自适应扰动抑制滤波器的本体振动控制

由于系统的非线性特征，挠性伸杆的振动不可能得到完全的抑制，而它的残余振动仍然会耦合作用到本体，所以在本体控制中设计自适应扰动抑制滤波器来进一步减小残余振动等效干扰力矩对本体的影响．

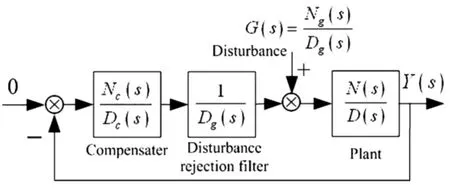
图4 基于内模原理的闭环扰动抑制系统Fig．4 Closed － loop disturbance rejection control system based on internal model principle

扰动抑制滤波器是基于内模控制原理的，内模控制原理是指将干扰的极点置于控制系统的内回路中，从而消除不稳定的干扰极点对系统输出的影响［8，9］，其原理如图 4 所示，干扰G(s)的极点对应于干扰的频率，此闭环控制系统的传递函数为

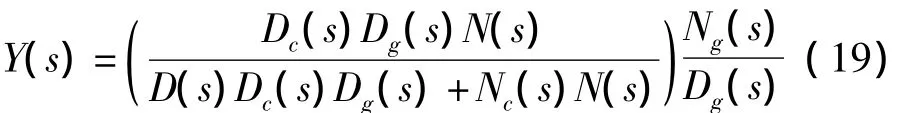
由式(19)可以看出干扰的极点被消除，从而达到抑制干扰的效果．

根据上述原理可将扰动抑制滤波器设计为

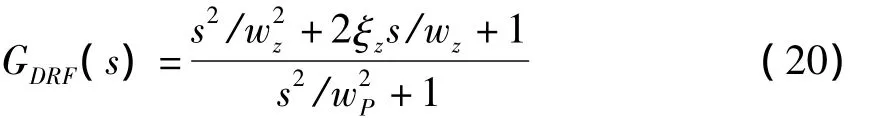
其中，wP就是系统的一阶模态振动频率，可通过计算和仿真得到．wz=kwp，k＜1，且当阻尼系数 ξz确定后，调节k的值使系统的响应时间和稳态精度达到最优．

扰动抑制滤波器原理简单、计算量小、易于实现，但其对变频干扰的鲁棒性较差，所以这里引入频率估计算法实时地调整滤波器的参数以提高其鲁棒性．卫星的姿态角速度信号中含有本体受到的振动干扰信息，稳态时姿态角速度信号可以用一正弦函数表示

其中wp就是振动干扰的频率，现对式(21)做如下变形处理［10］

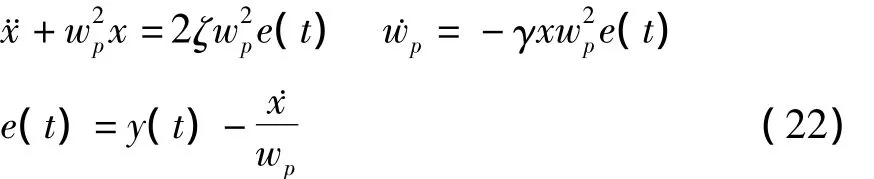
式中，x=－Acos(wpt+φ)，参数ζ和γ用于调节频率估计的精度和收敛速度．振动频率wp就可以作为一个状态量被估计出来，而后自适应地调节滤波器的参数以提高扰动抑制滤波器的鲁棒性．

3 仿真结果与分析

本体姿态控制的执行机构为基于金字塔构型的单框架控制力矩陀螺簇，忽略空间干扰力矩．小卫星的模型参数为

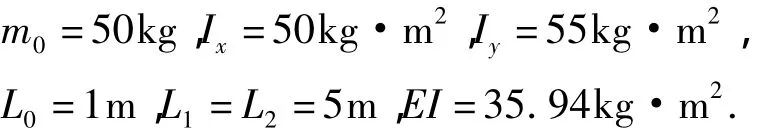
本体和挠性伸杆的PD控制参数分别为:

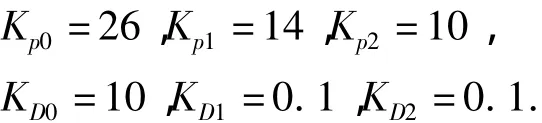
自适应扰动抑制滤波器的参数设置为:

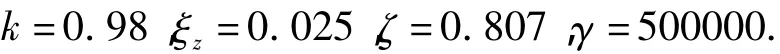
本体与伸杆的运动指令为:本体在100s内单轴机动20°，杆一、杆二在50s内分别转动20°．

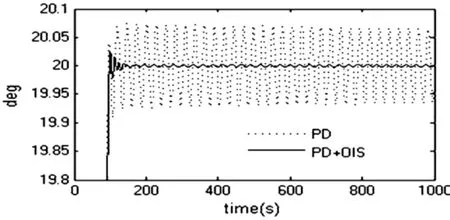
图5 本体姿态角Fig．5 Main body attitude angle

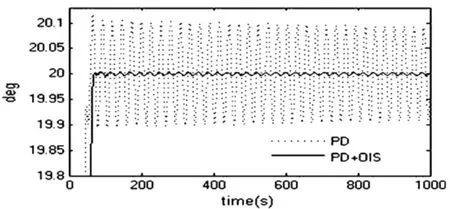
图6 关节转角1Fig．6 Joint angle of boom one

如图5～7所示，当只使用经典的PD控制器时，本体姿态角和两关节转角的控制精度并不高，分别只有 ±0．07°、±0．1°和 ±0．045°．而在挠性伸杆的控制器中加入最优指令整形器(OIS)后挠性伸杆的振动得到了大幅的抑制，两关节转角的控制精度分别提高到了 ±0．004°和 ±0．002°，从而卫星本体的姿态控制精度也提高到了±0．0025°．

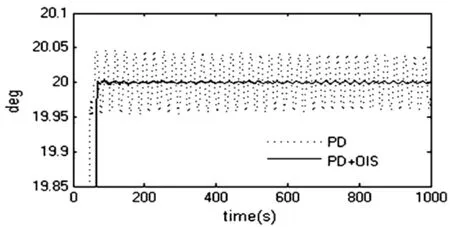
图7 关节转角2Fig．7 Joint angle of boom two

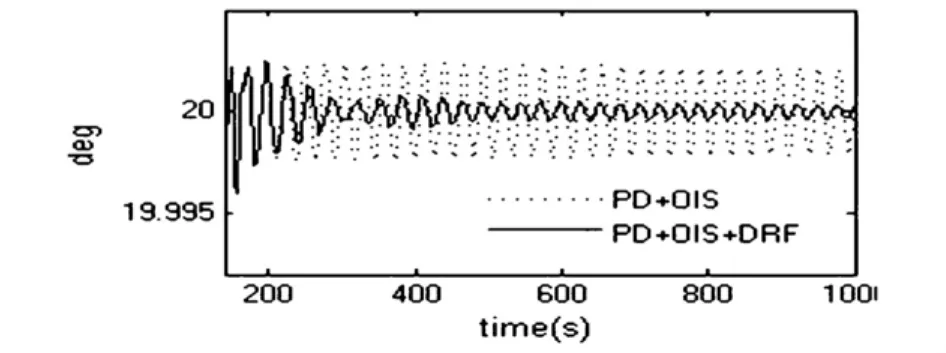
图8 基于本文复合振动控制方法的本体姿态角Fig．8 Main body attitude angle based on the proposed control method

由图8可以看出，ADRF进一步减小挠性伸杆的残余振动对航天器本体姿态控制的耦合影响，从而使卫星本体的姿态控制精度得到了进一步的提高，达到了 ±0．0006°．

4 结论

在最优指令整形器有效抑制挠性伸杆的低阶结构振动的基础上，卫星本体控制中的自适应扰动抑制滤波器进一步减小了挠性伸杆的残余振动对本体姿态控制精度的耦合影响．仿真结果表明，这种前馈补偿与反馈控制联合的控制策略，算法简单、计算量小、时滞小，为解决此类挠性卫星高精度姿态控制中的振动抑制问题提供了一种参考．

1 W Wang，P P Menonl，D G Batesi，et al．Robustness analysis of attitude and orbit control systems for flexible satellites．The Institution of Engineering and Technology，2010，4(12):2958～2970

2 Zeng Y，Araujo A D，Singh S N．Output feedback variable structure adaptive control of a flexible spacecraft．Acta Astronautica，2010，44(1):11～22

3 Rhim S，Book W J．Adaptive command shaping using adaptive filter approach in time domain．Proc Amer Contro Conf，San Digeo，CA，1999，6(1):81～85

4 孔宪仁，杨正贤，叶东等．基于指令整形的挠性航天器振动闭环抑制方法研究．振动与冲击，2010，29(3):72～77(Kong X R，Yang Z X，Ye D，et al．Feedback control in conjunction with input shaping for flexible spacecraft vibration suppression．Journal of Vibration and Control，2010，29(3):72～77(in Chinese))

5 Singhose W．Command shaping for flexible systems:A Review of the First 50 Years．International Journal of Precision Engineering and Manufacturing，2009，10(4):153～168

6 Chen Y，Meirovitch L．Control of a flexible space robot executing a docking maneuver．Journal of Guidance Controland Dynamics，1995，18(4):756～766

7 董明晓，梅雪松．时滞滤波器理论及其工程应用．北京:科学出版社，2008(Dong M X，Mei X S．Theory of time－delay filter and its engineering application．Beijing:Science Press，2008(in Chinese))

8 Wie B，Liu Q，Bauer F．Classical and robust control redesign for the hubble space telescope．Journal of Guidance Control and Dynamics，1993，16(6):1069～1077

9 Lau J，Joshi S S，Agrawal B N，et al．Investigation of periodic－disturbance identification and rejection in spacecraft．Journal of Guidance Control and Dynamics，2006，29(4):792～798

10 Mojiri M，Bakhshai A R．Estimation of n frequencies using adaptive notch filter．IEEE Transactions on Circuits and Systems，2007，54(4):338～342

*The project supported by the National Science Foundation of China(50905006)，and the Research Fund for the Doctoral Program of Higher Education(20091102120027)

† Corresponding author E－mail:ren．shanyong@163．com

COMPOSITE VIBRATION CONTROL METHOD FOR SMALL SATELLITE WITH FLEXIBLE BOOMS*

Ren Shanyong†Chu Zhongyi
(Science＆Technology on Inertial Laboratory，Key Laboratory of Fundamental Science for National Defense－Novel Inertial Instrument＆Navigation System Technology，Beihang University，Beijing100191，China)

In order to avoid the magnetic influence of satellite to the measurement information in the space detection missions，lightweight flexible booms are required to support various types of payload on their tip away from the satellite platform．While the elastic vibration of flexible booms will affect the attitude control accuracy of the satellite．Considering the complexity of appendages vibration and its effect on the satellite，an optimal input shaping(OIS)is applied to the flexible booms to suppress its low－order mode vibration，and then an adaptive disturbance rejection filter(ADRF)is designed to reject the disturbance caused by the residual vibration of booms further．Simulation results show that the proposed composite vibration control method can improve the satellite attitude control accuracy greatly．

flexible booms， optimal input shaping， adaptive disturbance rejection filter， composite vibration control

18 July 2012，

31 August 2012．

10．6052/1672－6553－2013－013

2012－07－18 收到第 1 稿，2012－08－31 收到修改稿．

*国家自然科学基金(50905006);教育部博士学科点专项基金(20091102120027)资助项目

E－mail:ren．shanyong@163．com