半车非线性悬架的非平稳随机振动及控制*

罗璇 靳艳飞

(飞行器动力学与控制教育部重点实验室，北京理工大学宇航学院，北京 100081)

半车非线性悬架的非平稳随机振动及控制*

罗璇 靳艳飞†

(飞行器动力学与控制教育部重点实验室，北京理工大学宇航学院，北京 100081)

研究了1/2车非线性悬架模型在路面随机激励下的非平稳振动响应，并基于随机最优控制理论对其进行主动控制．首先利用等效线性化方法将具有非线性阻尼及迟滞刚度的非线性悬架模型线性化，然后将主动、被动悬架非平稳随机响应进行比较，结果表明非线性主动悬架的性能要优于被动悬架．最后，通过Monte－Carlo数值模拟验证了理论结果．

非线性悬架， 非平稳随机响应， 等效线性化， 随机最优控制

引言

悬架系统的设计对于车辆的行驶平顺性、操纵稳定性及可靠性具有重要影响．相对于被动悬架，主动悬架具有高度的自适应性，已在一些车辆中得到应用并日益受到人们的重视．在主动悬架的研究中，不少的学者致力于针对线性主动悬架或四分之一车非线性悬架模型的研究［1－5］，研究了车辆非线性振动特性并设计了一些有效的控制方法，常用的有神经网络控制、模糊控制及自适应控制等．尽管非线性随机振动分析方法已有很大发展［6－7］，但还较少应用于车辆动态分析中．为了更好地反应车辆系统的动力学特性和实际工作情况，一些学者采用滤过白噪声来模拟路面的随机激励，分析车辆悬架系统的随机振动响应及最优控制［8－10］，但是大多局限于平稳随机激励下四分之一车的线性或非线性被动悬架系统的研究．然而，实际行驶中的车辆受到的路面不平度的随机激励很多情况下是非平稳的［11－12］，对于车辆非线性悬架系统的非平稳随机振动响应的分析较少．

本文考虑悬架系统的非线性特性，建立基于二分之一车悬架系统的动力学模型．采用一阶滤过白噪声来模拟路面的随机激励，利用等效线性化方法对非线性悬架的随机振动响应进行了分析，考虑了由于速度变化导致的系统非平稳响应情况，并基于随机最优控制理论对其进行主动控制．

1 悬架系统的非线性模型

1．1 动力学模型

考虑如图1所示的1/2车非线性主动悬架模型．其中，M是车身质量，J是车身俯仰转动惯量，m1，m2分别是前、后非簧载质量，c1，c2分别是前、后悬架线性阻尼系数，c'1，c'2分别是前、后悬架非线性二次方阻尼系数，前、后悬架具有迟滞特性弹簧的参数，ktf，ktr分别是前后轮胎刚度，a，b前轴、后轴到质心的距离．由图1可建立系统的运动微分方程组为:

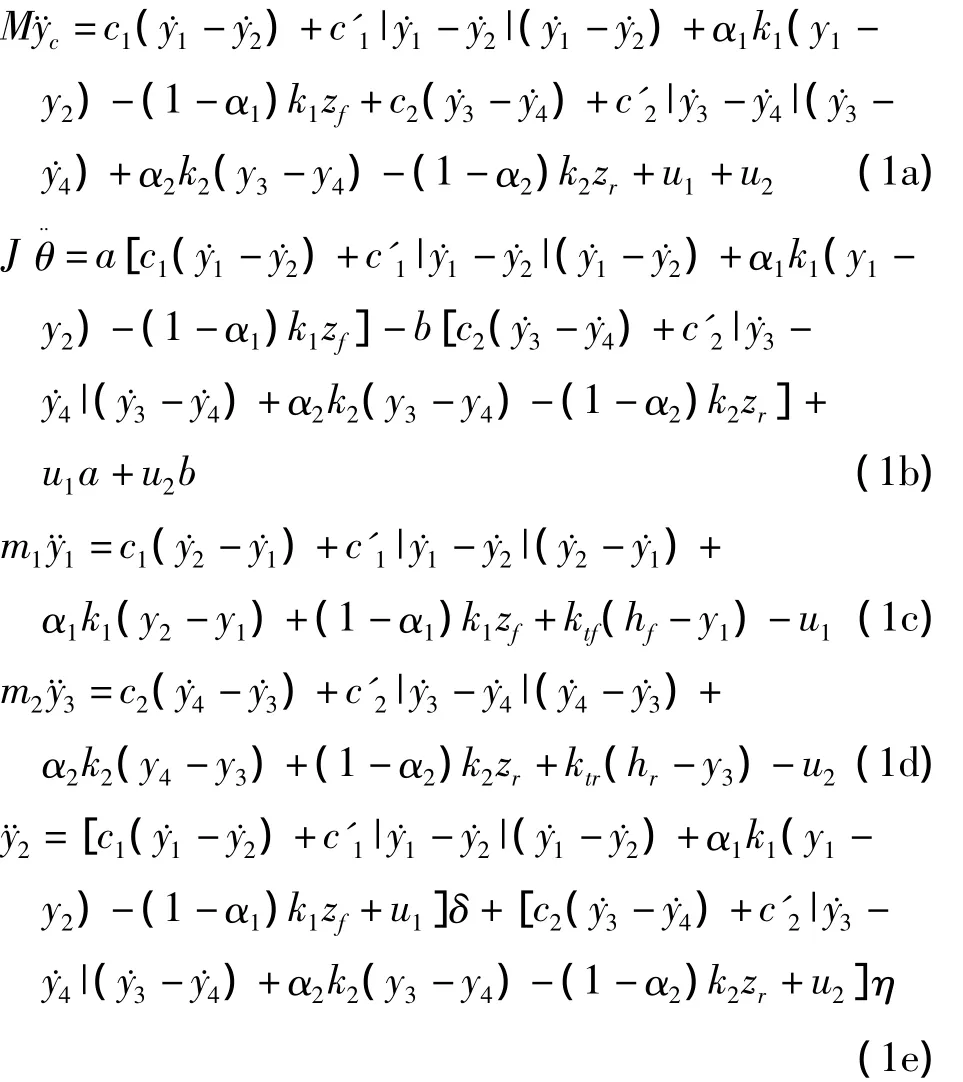
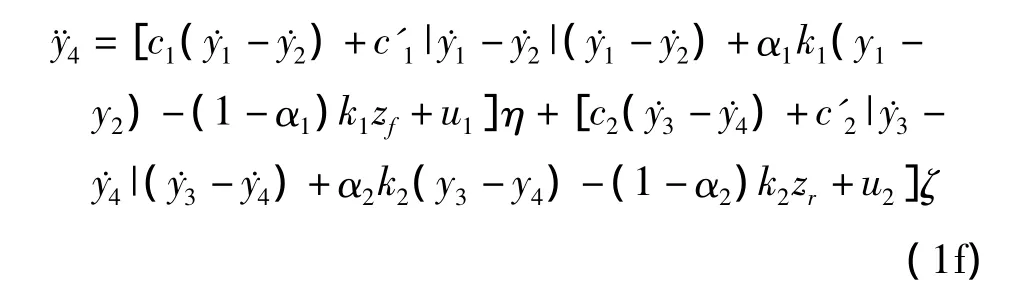
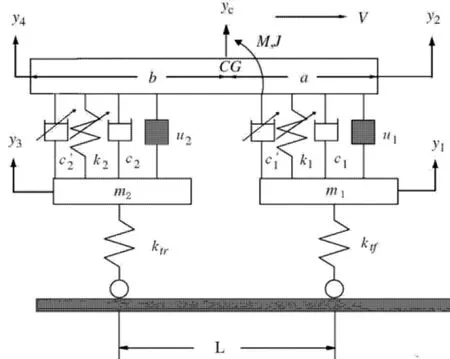
图1 1/2车非线性主动悬架模型Fig．1 Half－ car nonlinear suspension vehicle model

其中 δ=1/M+a2/J，η =1/M+ab/J，ζ=1/M+b2/J，y2=yc+aθ，y4=yc－bθ．y2，y4分别是车体前后端的绝对位移，y1，y3分别是前后簧载质量的绝对位移，hf，hr分别是前后轮的路面输入，u1，u2分别是前后控制力，α1，k1和 α2，k2分别是前后悬架迟滞特性弹簧参数，zf，zr分别是前后悬架迟滞位移．迟滞位移由下面的Bouc－Wen模型微分方程确定

其中 γf，βf，Af是前悬架迟滞参数，γr，βr，Ar是后悬架迟滞参数．这些参数和参数n影响迟滞力－位移曲线的形状和光滑度．

1．2 悬架模型的等效线性化

多自由度非线性系统的运动微分方程可表示为如下矩阵形式

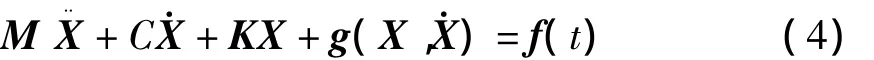
其中X是包括迟滞位移的状态矢量，f(t)为零均值n维 Gauss随机激励，g(X，)为表征系统本构关系的n维矢量非线性函数．

假设矢量非线性函数g(X，)各个元素gi都是自变量的单值奇函数．方程(4)可用等效线性系统来代替［6］

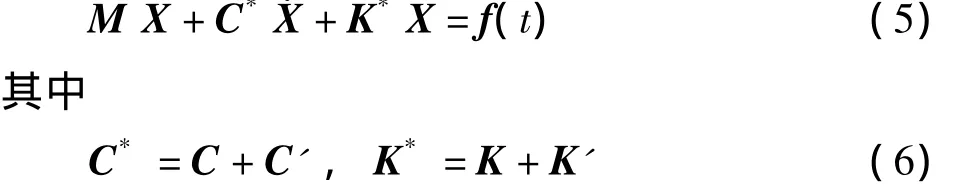
C和K分别表示线性阻尼与刚度矩阵，C'和K'分别为待定的等效阻尼及刚度矩阵．等效线性化目标是使系统(4)在一定意义下与系统(5)偏差最小，从而可取方程(5)的解作为方程(4)的近似解．常用的做法是使两方程之差

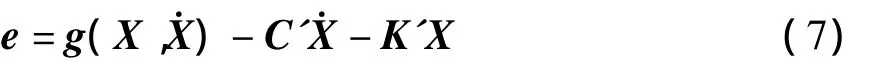
的均方值E［eTe］最小．

可以证明，使均方值E［eTe］最小的必要条件为

式中，ki和ci分别为矩阵K'和C'的第i行分量，z=［X］T．

当激励f(t)为Gauss随机过程时，等效线性系统(5)的响应也是Gauss随机过程．在此条件下，Atalik和Utku证明［7］等效参数可以显式表达．等效矩阵C'及K'的元素可表示为

应用上述结论，对1/2车四自由度悬架模型(1)－(3)进行等效线性化，可得

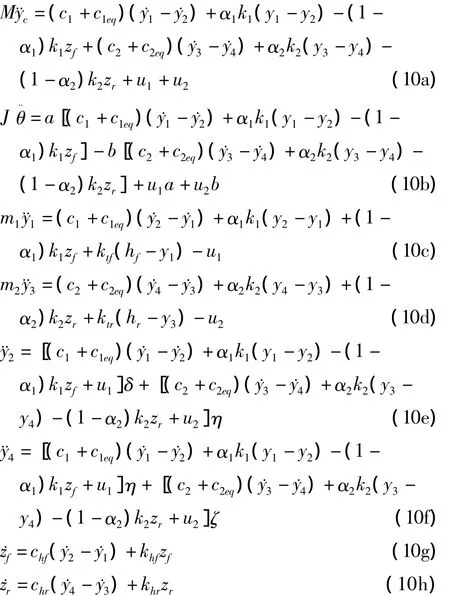
式中c1eq，chf，khf分别是等效的阻尼和刚度系数

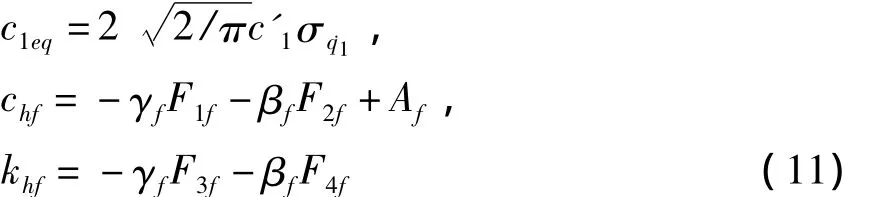
上式中的参数

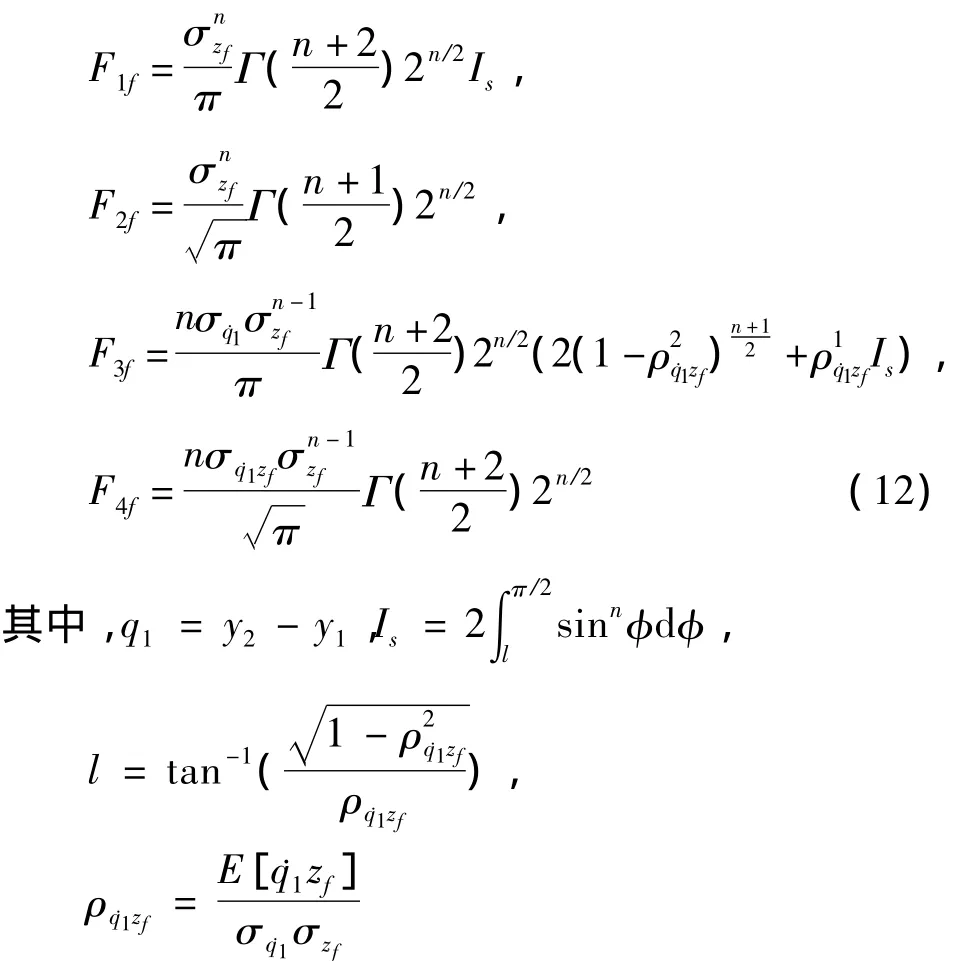
类似地，后悬架的等效参数c2eq，chr，khr也可由类似于(11)－(12)的等式给出．

2 路面随机激励模型

通常视路面不平度在空间上为白噪声的一阶滤波平稳输出［6］

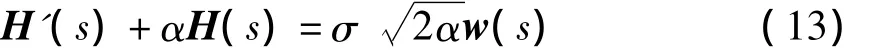
式中，'表示对道路走向长度s的微分，s表示车辆沿着路面的行程，α与σ均由路面等级决定的常量．当车辆以变速度行驶于路面时，此时路面不平度在时间域中不再是一平稳随机过程，其在时域中模型为

其中 H(t)=［hf(t)，hr(］T，w(t)=［w1(t)，w2(t)］T．w1(t)，w2(t)是零均值平稳高斯白噪声过程．w(t)的协方差矩阵可表示为E［w(t2)w(t1)］=Qδ(t2－t1)，Q是二阶单位矩阵．

3 悬架系统的最优控制

3．1 系统的状态空间描述

引入状态矢量Xa=［x1x2x3x4x5x6x7x8x9x10x11x12］T，x1=y1;x2=y1;x3=y2;x4=y2;x5=y3;x6=y3;x7=y4;x8=y4;x9=zf;x10=zr;x11=hf;x12=hr．将悬架系统等效线性化方程(10)－(12)及路面输入模型(14)联合表示为

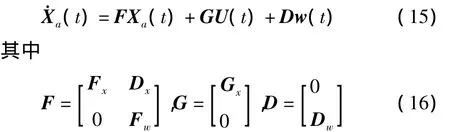
3．2 最优控制算法

悬架系统最优控制的目标是在综合考虑前后悬架的乘坐舒适性、悬架动挠度、操纵稳定性和控制能量情况下提高悬架的总体性能指标．非平稳响应控制是有限时间最优控制问题，悬架系统的综合性能指标为

其中J1=E［］+E［］为车体前后端加速度均方值以衡量乘坐舒适性;J2=E［(y1－y2)2］+E［(y3－y4)2］为悬架动挠度均方值;J3=E［(y1－hf)2］+E［(y3－hr)2］为轮胎变形量均方值用来衡量操纵稳定性;J4=E［］+E［］为系统反馈控制力均方值;ρ1、ρ2、ρ3、ρ4为相应的权系数;S1=S(t1)为对称的终态权矩阵;(t0，t1］为控制时间．

将综合性能指标变换成标准形式，如下式

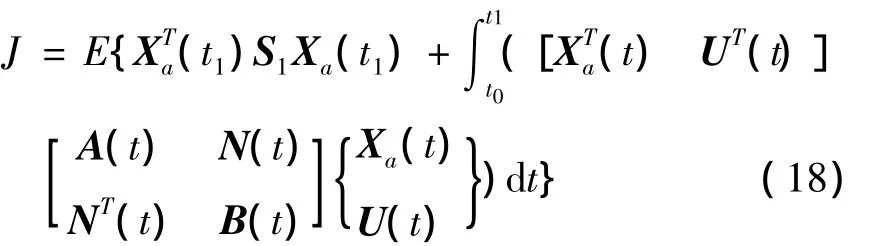
其中矩阵A(t)，B(t)分别为对称的半正定和对称正定矩阵．

假定系统的状态向量Xa(t)在t时刻是完全可测的，则求解以上线性随机最优控制问题随机最优控制律为［13］

其中C(t)是反馈控制增益矩阵，由下式给出

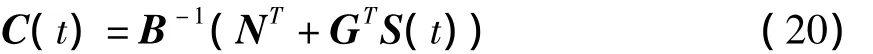
式中，S(t)是对称的半正定矩阵，是如下Riccati矩阵方程的解令上述方程的终态值为S(t1)．

系统响应的方差矩阵 P(t)=E［Xa(t)XTa(t)］，是如下Lyapunov矩阵微分方程的解

令上述方程的初始条件为P(t0)，是t=t0时的方差矩阵．

Riccati矩阵方程(21)是已知终时状态值的微分方程组，对其求解需要进行逆序积分．由于矩阵F与系统的响应统计量有关，而Riccati矩阵方程的求解同时又与系统矩阵F有关，需要通过迭代求得系统响应统计量．首先计算线性悬架(忽略所有非线性因素)的反馈控制增益矩阵C(t)，再由C(t)求解非线性悬架的响应统计值．然后利用当前的响应统计值求解非线性悬架的控制增益矩阵．重复进行此迭代过程，直至任意时刻下控制增益矩阵中各分量与响应统计量都收敛．

求得控制增益矩阵C(t)和系统响应的方差矩阵 P(t)后，各个性能指标J1，J2，J3，J4可表示为:

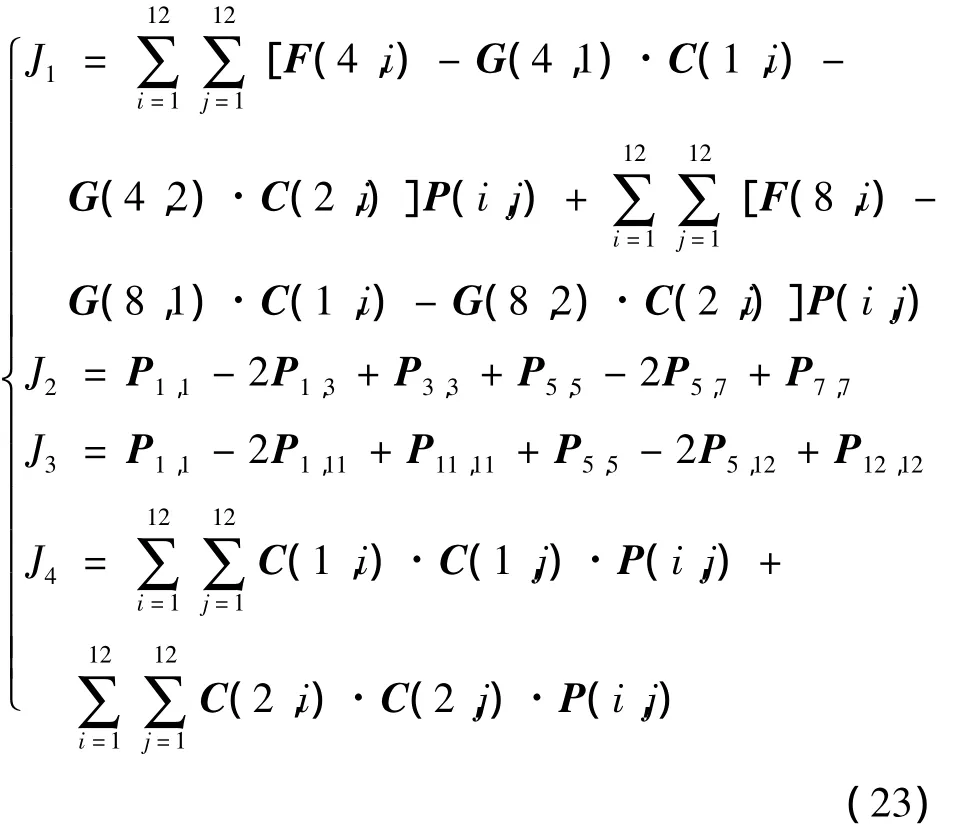
3．3 初始条件

在求解Lyapunov矩阵方程(22)的过程中，需要给出初始条件P(t0)的值．假定车辆由静止开始进行匀加速运动．由于路面不平度为空间上的均匀随机场，则有

由于初始时刻车辆处于静止状态，有

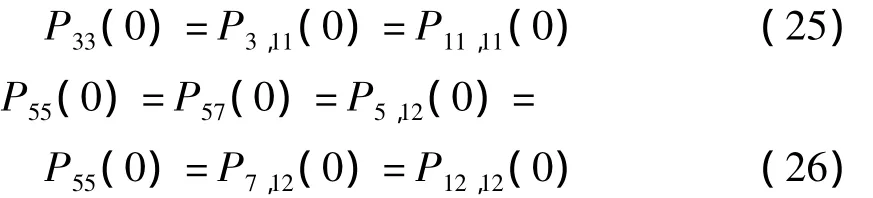
考虑到方差矩阵P(t)的对称性，有

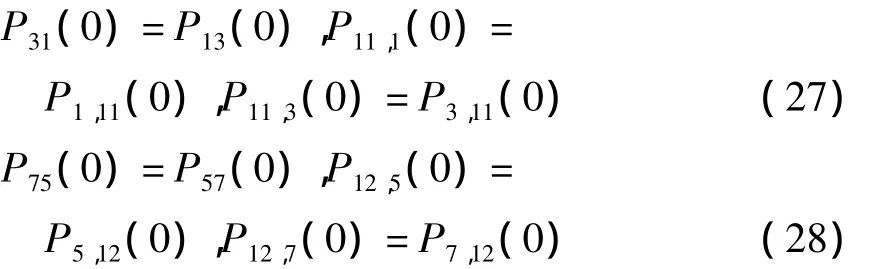
P(0)中其余分量为零．

3．4 计算结果及分析

1/2车非线性悬架模型的参数选取为:

权系数选取为 ρ1=1，ρ2=104，ρ3=104，ρ4=10－6．Bouc－Wen迟滞模型的参数为:α1=α2=0．2，γf=γr=0．5，βf=βr=0．5，Af=Ar=1．5 选取路面参数为:α =0．12m－1，σ =15mm．

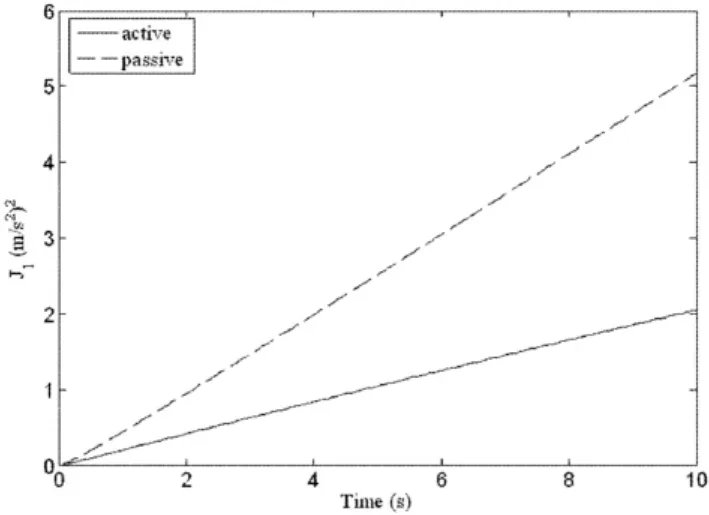
图2 簧载质量加速度均方值Fig．2 The rms sprung mass acceleration

图3 悬架动挠度均方值Fig．3 The rms stroke responses

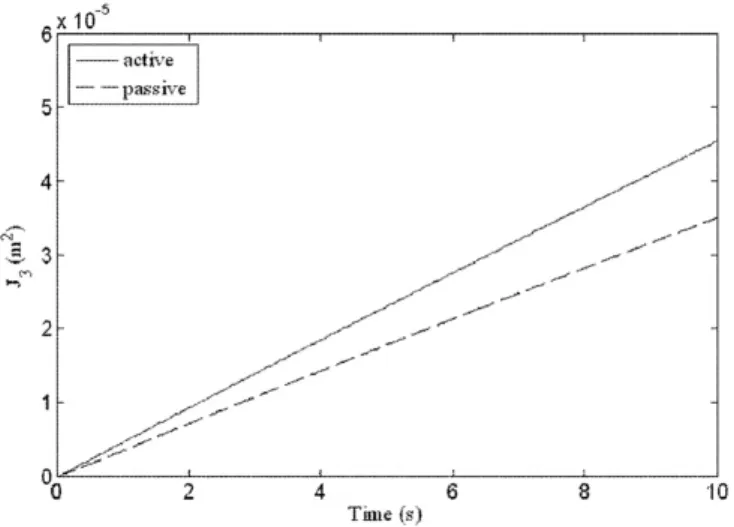
图4 轮胎变形量均方值Fig．4 The rms values of the tyre deflection

图5 控制力均方值Fig．5 The rms values of the control force

图6 悬架综合性能指标Fig．6 The overall performance of the suspension

图2－6给出了主动悬架与被动悬架在ac=2m/s2下各个性能指标的比较．图2为乘坐舒适性指标J1随时间的变化情况，可以看出主动悬架的乘坐舒适性要明显优于被动悬架;随着时间的增长，被动和主动悬架的乘坐舒适性都会逐渐恶化，但主动悬架的乘坐舒适性指标的变化相对被动悬架要缓慢．图3为悬架动挠度均方值J2随时间的变化，结果与图2相似．图4为轮胎变形量均方值J3随时间的变化情况，被动悬架的操纵稳定性要稍好于主动悬架，可能是由于本文所考虑的权系数更侧重于乘坐舒适性导致的．图5为控制力均方值J4随时间的变化，随着时间的增加主动悬架所需的控制力变大．图6为主动悬架与被动悬架的综合性能指标J随时间的变化，可以看出虽然在操纵稳定性上主动悬架的表现略差于被动悬架，但主动悬架能很好地改善悬架的综合性能和其他性能指标．

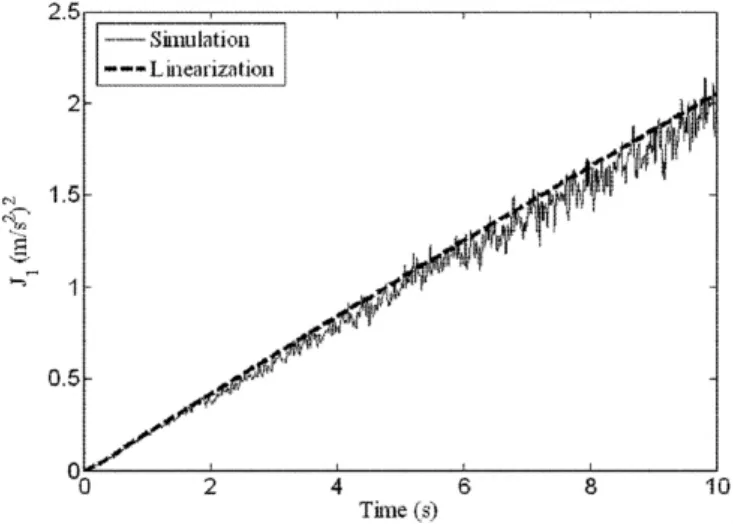
图7 簧载质量加速度均方值Fig．7 The rms sprung mass acceleration

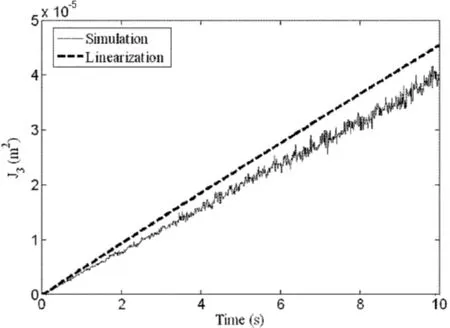
图9 轮胎变形量均方值Fig．9 The rms values of the tyre deflection

为验证等效线性化方法的可行性及精确性，利用Monte－Carlo模拟对1/2车非线性悬架系统非平稳随机响应进行验证．以匀加速情况下的主动悬架为例进行说明，见图7－11．可以看到等效线性化结果与数值模拟结果基本吻合，表明等效线性化方法能有效处理随机激励下的非线性被动悬架系统和基于随机最优控制的主动悬架的非平稳响应分析，且计算量和计算时间要远远小于数值模拟方法．

图10 控制力均方值Fig．10 The rms values of the control force

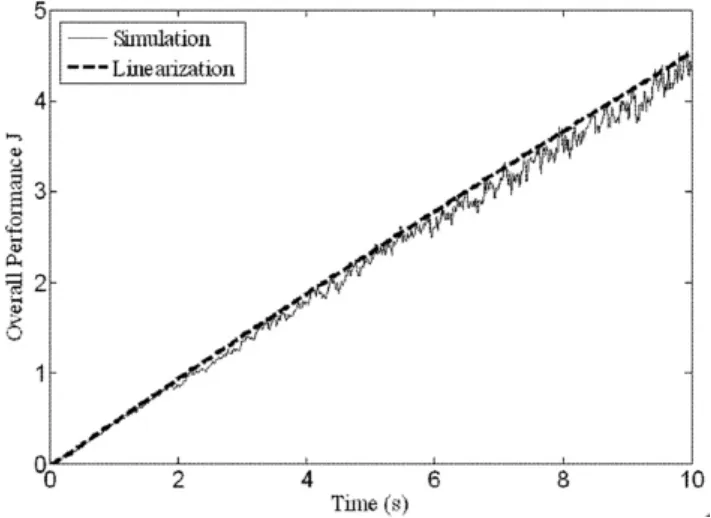
图11 悬架综合性能指标Fig．11 The overall performance of the suspension

4 结论

本文研究了具有二次阻尼和迟滞刚度的1/2车非线性悬架系统的非平稳随机响应及主动控制问题．利用等效线性化方法研究了考虑路面随机激励输入时，非线性主动悬架系统的近似响应量．结果表明:在本文考虑的权系数下，相对被动悬架，主动悬架能很好地改善乘坐舒适性，悬架动挠度和系统的综合性能，但操纵稳定性略有恶化．最后，采用数值模拟方法验证了等效线性化方法的有效性，说明等效线性化方法可以有效处理迟滞系统在随机激励下的响应计算．

1 张庙康，胡海岩．车辆悬架振动控制系统研究的进展．振动、测试与诊断，1997，17(1):7 ～15(Zhang M K，Hu H Y．A review of recent advances in research and development of vibration controls on vehicle suspension system．Journal of Vibration，Measurement＆Diagnosis，1997，17(1):7～15(in Chinese))

2 钟顺，陈予恕．分段线性非线性汽车悬架系统的分岔行为．应用数学和力学，2009，30(6):631 ～638(Zhong S，Chen Y S．Bifurcation of piecewise－linear nonlinear vibration system of vehicle suspension．Applied Mathematics and Mechanics，2009，30(6):631 ～638(in Chinese))

3 郭大蕾，胡海岩．基于磁流变阻尼器的车辆悬架半主动控制研究－建模与直接自适应控制．振动工程学报，2002，15(1):10 ～ 14(Guo D L，Hu H Y．Semi－active control of vehicle suspensions based on magnetorheological damper:modeling and directive adaptive control．Journal of Vibration Engineering，2002，15(1):10 ～ 14(in Chinese))

4 Thompson A G．An active suspension with optimal linear state feedback ．Vehicle System Dynamics，1976，5(4):187～203

5 江雄．四分之一车模型的非线性悬架随机最优控制．［博士学位论文］南京:南京航空航天大学，2009(Jiang X．Stochastic optimal control of nonlinear suspension of quarter Car Model［PhD Thesis］．Nanjing:Nanjing University of Aeronautics and Astronautics，2009(in Chinese))

6 方同．工程随机振动．北京:国防工业出版社，1995(Fang Tong．Engineering random vibration．Beijing:National Defense Industry Press，1995(in Chinese))

7 Atalik T S，Utku S．Stochastic linearization of multi－degree－of－freedom nonlinear systems．International Journal Earthquake Engineering and Structural Dynamics，1976，4:411～420

8 Wagner U Von．On nonlinear stochastic dynamics of quarter Car Models．International Journal of Nonlinear Mechanics，2004，39:753～765

9 Gopala Rao L V V，Narayanan S．Sky－hook control of nonlinear quarter car model traversing rough road matching performance of LQR control．Journal of Sound and Vibration，2009，323:515～529

10 Turkay S，Akcay H．A study of random vibration characteristics of the quarter car model．Journal of Sound and Vibration，2005，282:111～124

11 曹友强，罗红，董红亮．主动悬架最优控制性能函数的加权系数研究．系统仿真学报，2007，19(23):5459～5462(Cao Y Q，Luo H，Dong H L．Study on weight number of performance function by optimum control for active suspension．Journal of System Simulation，2007，19(23):5459～5462(in Chinese))

12 陈无畏，沈云鹤，张启群．汽车主动悬架的最优控制及计算机仿真．振动与冲击，1996，15(4):53～58(Chen W W，Shen Y H，Zhang Q Q．The optimal control and computer simulation of active suspension for automobile．Journal of Vibration and Shock，1996，15(4):53 ～58(in Chinese))

13 Kwakernaak H，Sivan R．Linear optimal control systems．New York:John Wiley and Sons Inc，1972

17 April 2012，

14 June 2012．

*This work was supported by the National Natural Science Foundation of China under(10972032，11272051)and the Excellent Young Scholars Research Fund of Beijing Institute of Technology under(2010YS0101)

† Corresponding author E－mail:jinyf@bit．edu．cn

NON-STATIONARY RANDOM VIBRATION AND OPTIMAL ACTIVE CONTROL OF A HALF-CAR NONLINEAR SUSPENSION*

Luo Xuan Jin Yanfei†
(Key Laboratory of Dynamics and Control of Flight Vehicle Ministry of Education，School of Aerospace Engineering，Beijing Institute of Technology，Beijing100081，China)

This paper studied the non－stationary stochastic response and the optimal control of a half－car dynamical model with nonlinear active suspension under the excitation of random road surface．Using the method of equivalent linearization，the response statistics and stochastic optimal control of the nonlinear suspension were obtained．The comparison and analysis of the non－stationary response of active and passive suspension show that the nonlinear active suspension is better than the passive suspension．Finally，the accuracy of the equivalent linearization technique was verified by Monte Carlo simulation．

nonlinear suspension， non－stationary random response， equivalent linearization， stochastic optimal control

10．6052/1672－6553－2013－012

2012－04－17 收到第 1 稿，2012－06－14 收到修改稿．

*国家自然科学基金(10972032，11272051)、北京理工大学优秀青年教师资助计划持续支持项目(2010YS0101)资助

E－mail:jinyf@bit．edu．cn