含磨损故障的齿轮传动系统非线性动力学特性

王晓笋，巫世晶，周旭辉，胡基才

(1.武汉大学 动力与机械学院，武汉 430072;2.武汉第二船舶研究所，武汉 430064)

齿轮传动系统是目前机械系统中使用最为广泛的传动方式，其通过轮齿啮合实现载荷和运动的传递［1］。而由于其内部存在的齿侧间隙、时变啮合刚度和内部误差激励等非线性因素，使得齿轮传动系统的负载运行的过程中呈现复杂的非线性动力学特征。Kahraman等［2－4］考虑了齿侧间隙和轴承间隙等非线性因素，建立单级齿轮传动系统单自由度、二自由度和三自由度非线性动力学模型，应用解析法和数值法对模型进行求解，发现系统存在的跳跃不连续和混沌等典型非线性现象。Theodossiades等［5］和 Raghothama 等［6］分别采用多尺度法和增量谐波平衡法对齿轮传动系统非线性动力学模型进行了求解，发现了系统存在的亚谐波共振和超谐波共振现象。刘梦军等［7］采用数值积分的方法研究了单级齿轮传动系统所具有的分岔与混沌现象。Kahraman 等［8］和 Parker等［9］分别建立了齿轮传动系统非线性动力学试验系统，通过试验测试获得的幅频特性曲线验证了系统存在的跳跃不连续现象。Cai等［10－11］考虑了齿轮传动系统的非线性支撑力，通过数值积分的方法研究了啮合阻尼和激励频率对于齿轮传动系统振动特性的影响。

而轮齿在运行的过程中由于受到载荷和齿面润滑状态的影响，齿面会出现不间断的磨损现象。齿面磨损的直接结果是导致齿面金属材料的非均匀去除［12］，但同时也会进一步引起齿轮传动系统振动与噪声的加剧［13］，由此可能使得轮齿的动载荷急剧增加，并由此可能引起轮齿受到更大的冲击载荷作用，最终将导致轮齿折断。分析含有磨损故障特征的齿轮传动系统非线性动力学特性是揭示齿轮传动系统在出现磨损之后会出现早期失效的有效途径之一。为此，本文考虑了齿面磨损可能引起的直齿轮传动系统的特性参数的变化，建立了含有齿面磨损故障的齿轮传动系统非线性动力学模型并对其进行数值特性分析，以变步长积分方法计算获取了系统的分岔图和对应的李雅普诺夫指数谱，由此分析系统在某个关键参数变化时的全局非线性动力学特性。同时，通过Poincaré映射、功率谱对系统出现的周期、拟周期和混沌运动进行深入细致地研究，揭示系统由周期经分岔进入混沌的途径以及非线性系统内部所蕴含的一些普适性规律。

1 三自由度动力学的模型

一对直齿轮的三自由度平移－扭转耦合的动力学模型如图1所示，模型中θ表示角位移，y表示竖直方向位移，k表示刚度，c表示阻尼，I表示转动惯量，m表示质量，R为基圆半径，T表示扭矩，F表示力，e表示内部误差激励。下标g1，g2，b1，b2分别代表主从动齿轮和主从动齿轮的支撑轴承，h表示啮合齿轮对，eq代表等效。符号“—”表示带有量纲的变量。为消除系统内存在的刚体位移，引入轮齿之间动静态传递误差之差，由此建立齿轮传动系统三自由度动力学方程如式(1)所示。

图1 三自由度直齿轮传动系统动力学模型Fig.1 Three-degree-of-freedom dynamic model of a spur gear pair transmission system

引入标称尺度bc和时间尺度t=ωn，无量纲广义坐标表示为ybi=bi/bc(i=1，2)，δ=/bc，可以得到方程式(1)的无量纲形式如式(2)所示。

Kahraman等［2］通过研究发现，轴承的间隙与齿轮的齿侧间隙均可以用分段非线性函数描述，其中主动轴轴承和从动轴轴承的间隙可以描述为:

齿侧间隙可以描述为:

2 齿面磨损故障特征的引入

2.1 齿面累积磨损量的计算

为研究齿面磨损对于系统动力学特性的影响，首先采用Archard公式［12］计算齿面动态磨损特性，主要考虑轮齿啮合的动载荷、啮合点滑移速度等计算轮齿负载运行一定周期之后的累积磨损量，其中主从动齿轮齿面的累积磨损量可以描述为:

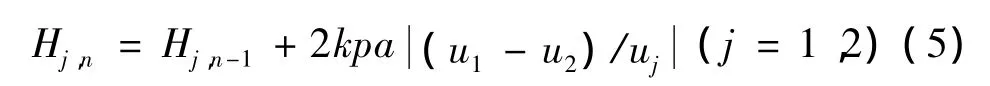
式中:uj(j=1，2)为主从动齿轮的滚动速度，k和p分别为当前啮合点的动态磨损系数和最大接触力，α为当前啮合点处Hertz接触宽度。

2.2 轮齿啮合刚度的计算

根据 Weber-Banaschek公式［17］，单个轮齿中线和啮合线的交点(图2中P点)在啮合线方向的变形量包括弯曲剪切变形量 δZ，基础部分变形量 δR和由于轮齿接触而产生的载荷作用点到 P点的接近量 δpW。δZ，δR和 δpW可以分别采用式(6a)，(6b)和(6c)计算获取。一对轮齿啮合时，轮齿在啮合线方向总体变形量与啮合刚度分别用式(6e)和(6f)表示。

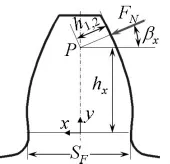
图2 轮齿的几何参数Fig.2 Geometry parameters of Gear Tooth

式(6(a)～(d))各参数如图2所示，E为等效弹性模量，b为齿宽，ρ1和ρ2为接触点的当量圆柱体半径。

齿面累积磨损造成渐开线齿廓的变化，为此在式6((a)～(c))中引入从动齿轮的齿面累积磨损量H1和H2，由此计算出现磨损之后轮齿的啮合刚度。

2.3 算例

取主动齿轮齿数z1=30，从动齿轮齿数z2=40，模数 m=4，齿宽 b=0.03，标准压力角 φ =20°，输入力矩Tin=60 N·m，输出负载为Tout=80 N·m，主从动齿轮弹性模量 E1=E2=207 GPa，a=1.33 ×10－8(m2/N)，磨损系数 k=5 × 10－16(m2/N)［12］，通过式(5)计算获得轮齿运行105次之后的累积磨损量沿啮合线的分布如图3所示，在节点附近的单齿啮合区间内磨损量最小，因为单齿啮合区间内虽然载荷由单个轮齿承担，但滑移速度较小，因而最终的累积磨损量相对较小;在靠近齿顶处的双齿啮合区间1和靠近齿根处的双齿啮合区间2的磨损量则相对较大，特别在齿顶处累积磨损量是整个轮齿上最大的。

图3 啮合齿轮对齿面累积磨损量Fig.3 Accumulated surface wear of gear pair

采用式(6(a)－(f))计算获得齿轮对啮合刚度如图4所示，齿轮对啮合刚度与磨损量一样分为双齿啮合区间1、单齿啮合区间和双齿啮合区间2。考虑啮合齿轮对长期负载运行之后出现较为严重的磨损，对比未磨损的齿轮对啮合刚度和出现磨损之后的啮合刚度可以发现，沿渐开线齿廓不均匀分布(如图4所示)磨损量使得单个轮齿的啮合刚度在齿顶和齿根位置减小，但在节点处变化相对较小。

图4 未磨损与出现磨损的轮齿时变啮合刚度Fig.4 Time-varying mesh stiffness of worn and unworn gear pair

3 非线性系统的数值特性分析

在建立齿轮传动系统动力学方程时，时变啮合刚度通常进行一定的简化处理，将图4所示的啮合刚度以一系列三角函数和的形式进行描述，从而便于求解处理。本文采用Raghothama等［6］提出的式(7)表达时变啮合刚度，由于齿面磨损引起的啮合刚度的变化通过分析发现主要体现在εr在上。通过对图4的磨损齿轮对的啮合刚度进行傅里叶级数展开，可以得到一系列的εr在值，本文取r=3。

系统的诸多非线性因素会引起系统可能出现周期、拟周期和混沌响应，为全面获得系统的动力学响应特性，本文采用了典型的定性和定量分析方法，其中分岔图采用基于闪频(Stroboscopic)原理，能够观察系统随某一个关键参数变化经由周期进入混沌的途径，也可以发现系统的周期运动区域和混沌运动区域;但对于系统是否为拟周期或混沌运动通过分岔图则不易判断，而对于多自由度系统是否处于超级混沌状态也不能够由分岔图加以判断，为此，需要利用李雅普诺夫指数谱进行区分，本文引入 Wolf等［14］提出的 GRAMSCHMIDT正交化方法计算多自由度系统的李雅普诺夫指数谱。其它定性分析方法，如自相关功率谱和Poincaré映射等则能够准确描述系统在某一特定参数设置下的动态响应特性，可作为分岔图和最大李雅普诺夫指数谱计算结果的重要验证方法。

本文所建立的三自由度齿轮传动系统属于强非线性系统，为此采用变步长的Gill积分方法对系统的动力学方程(式(2))进行数值积分计算。非线性系统对于初值具有敏感性特征，同时系统在起始阶段还具有瞬态响应。为确保数值计算的结果为系统的稳态响应，将开始的800个周期的解舍弃，利用800周期之后数值积分结果获取分岔图、Poincaré映射和功率谱曲线。系统的动力学方程(式(2))中的各个参数取值分别为 ζ11= ζ22=0.01，ζ33= ζ23=0.012 5，ζ33=0.05，k11=k22=1.25，Fb1=Fb2=0.1，Fm=0.3，FaH=0.6，bb1=bb2=0，bc=bh=0.12 mm，ε1=0.3，ε2=0.1，ε3=0.05。对式(2～4)进行数值积分求解，选取的初始条件为初始位移为0.1，初始速度为0，系统的无量纲激励频率Ω从0.7增加到2.7，获得系统的分岔图与李雅普诺夫指数谱如图5所示。Eckmann［15］归纳出走向混沌的3种途径:Feigenbaum途径，Ruelle-Takens-Newhouse途径和Pomeau-Manneville途径。从计算的结果可以发现，随着激励频率Ω的变化，系统出现了多个周期运动、拟周期运动和混沌运动区间，而上述3种进入混沌的典型途径在分岔图上都可以发现，但是系统由于系统内部存在着多种间隙，进入混沌主要通过倍周期分岔以及不同形式的拟周期经由锁相进入混沌的途径。

图5 随激励频率变化的分岔图与对应的李雅普诺夫指数谱Fig.5 The bifurcation diagram and the corresponding Lyapunov exponents of the system with the excitation frequency as the vary parameter

3.1 倍周期分岔途径

通过倍周期序列进入混沌是非线性系统的常规途径，其特点为系统的响应的周期数目随参数变化而不断加倍，最终进入混沌。从分岔图中可以发现，在激励频率区间 Ω∈［1.34，1.4］这个区间内存在这一个倍周期分岔序列(按照激励频率从大到小的变化趋势)。

图6 系统的Poincaré映射Fig.6 Poincaré maps

图7 系统的功率谱Fig.7 The power spectrums

系统从周期1运动开始(图6(a))，经过不多的周期加倍，经历周期2(图6(b))，周期4(图6(c))，周期8(图6(d))和周期16(图6(e))，最终系统进入混沌运动(图6(f))。在Poincaré映射上，周期n运动对应这n个不动的离散点，而功率谱则对应着在1/n基频及m/n(m为正整数)处存在尖峰(图7(a)～(e))。当系统进入混沌运动之后，Poincaré映射上出现了奇怪吸引子(图6(f))，功率谱曲线则表现为具有噪声背景的连续谱，同时在1/8及m/8基频处存在尖峰，表明了系统访问奇怪吸引子8个不同区域的严格周期性(图7(f))。通过相轨线、Poincaré映射和功率谱的计算结果验证了分岔图与李雅普诺夫指数谱的正确性。

3.2 拟周期分岔途径

通过拟周期分岔进入混沌是系统存在的主要途径之一，在分岔图上可以观察到多个经由拟周期分岔途径进入混沌的区域，而各个不同区域其具体的分岔途径又存在差异，下面选取两个具有代表意义的拟周期途径进行分析。

3.2.1 拟周期分岔途径1

在区间 Ω∈［1.2，1.22］存在着一个典型的拟周期进入分岔的途径，当系统的激励频率Ω=1.22时，系统处于周期2运动状态，如图8(a)所示，此时Poincaré映射上是两个稳定的焦点，功率谱上对应m/2倍基频处存在着尖峰图9(a)。随着激励频率的变化，当Ω=1.217 2时，稳定的焦点失去稳定性，并经由Hopf分岔变成两个吸引环图8(b)，此时，除了在m/2倍基频处存在着尖峰，分析其频域特性，如图9(b)所示，系统的频域上存在1/7，2/9，3/11，9/23 等一系列不可约频率分量，而通过研究发现这些频率分量之间存在着以下关系:

这表明在系统的拟周期频域区间的频率分量之间满足周期相加法则［16］(period-adding law)。继续改变激励频率，系统Poincaré映射上的吸引环呈现面积不断增大的趋势(图8(b))，再次观察功率谱曲线(图9(b))可以发现系统的响应上出现了更多的频率分量。随后Poincaré映射上的吸引环开始发生变形(图8(c))和环面上的自缠绕(图8(d))，系统的功率谱上出现了更多不可公约的特征频率(图9(c)～(d))。环面上的拟周期运动逐渐失去稳定性，此时稍有扰动就会过渡到另外一个周期解，拟周期运动中的两频率之比将从无理数变成与之接近的有理数，当Ω=1.207现，系统出现了周期8响应(图8(e))，频率谱上(图9(e))也出现了m/8基频处出现了尖峰。最终通过多周期锁相进入混沌状态(图7(f))，系统的功率谱变成了具有噪声背景的连续谱(图9(f))，对应在Poincaré映射上也出现了具有分维数的奇怪吸引子。特别的，在功率谱上面对应m/2基频处也存在着尖峰，代表系统周期性的访问Poincaré映射上的两个混沌区间。这种经过周期运动→拟周期→锁相→混沌是系统进入混沌的常规途径之一。

3.2.2 拟周期分岔途径2

在区间 Ω∈［1.8，1.82］也存在拟周期分岔进入混沌的途径，随着激励频率Ω的改变，Poincaré映射上首先出现的是多周期离散点(图10(a));此时系统处于周期13运动状态，接着周期运动通过Hopf分岔被拟周期运动替代，Poincaré映射出现了具有扭曲缠绕特性的T1环面(图10(b));不稳定的拟周期运动再次进入P107多周期运动状态，即锁相(图10(c));随后是进一步扭曲变形的T1环面(图10(d));不稳定拟周期运动再次被P94多周期运动所替代(图10(e));从图10可以发现，系统经历了多次类似拟周期和多周期锁相的交替出现，即具有扭曲T1环面的拟周期运动(图10(f))→P81多周期锁相(图10(g))→扭曲T1环面的拟周期运动(图10(h))→P136多周期锁相(图10(i))→扭曲T1环面的拟周期运动(图10(j))→P55多周期锁相(图10(k))。最终系统在经历上述多次拟周期→多周期锁相之后，在Poincaré映射出现了具有连续功率谱的混沌运动(图10(l))。这种经历多次拟周期→多周期锁相的通向混沌的演化路径是非常规通路，说明了含有磨损故障齿轮传动系统经由拟周期运动通向混沌的复杂性和多样性。

图8 系统的Poincaré映射Fig.8 Poincaré maps

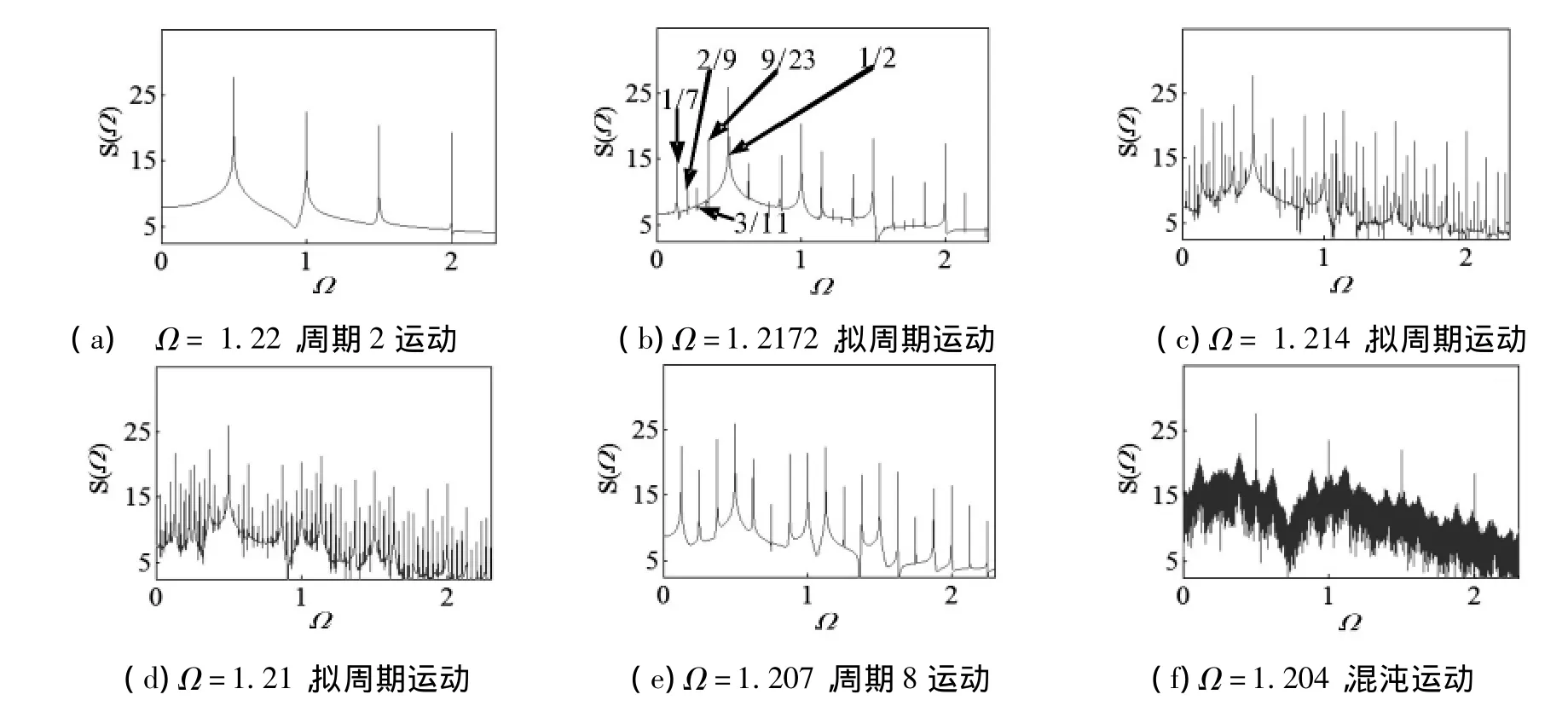
图9 系统的功率谱Fig.9 Power spectrus

同时，还可以发现嵌套在拟周期运动区间内相邻的多周期运动之间周期数存在一个有趣的现象，相邻三个周期运动中间一个的周期数等于第一个和第三个周期运动周期数之和，当Ω=1.807 5，系统处于周期13运动(图10(a));而当Ω=1.814 8，系统处于周期94运动(图10(e))，在这两个周期窗口之间，当 Ω=1.813 6，存在着一个周期107运动区间(图10(c))，而107=13+94。同时，系统另外三个嵌套在拟周期运动区间的多周期窗口也满足上述规律，当Ω=1.816 8，系统处于周期81运动(图10(g));而当Ω=1.821，系统处于周期55运动(图10(k))，在这两个周期窗口之间，当Ω=1.818 8，存在着一个周期136运动区间(图10(i))，而136=81+55。从分岔图和李雅普诺夫指数谱上还可以发现，在系统进入混沌运动之后，混沌振动区间内依然间或出现了大量的多周期窗口，这种交替出现的混沌、多周期运动最终导致了超级混沌运动的出现，对应的李雅普诺夫指数谱具有［+，+，－，－，－，－］的形式。

图10 系统的Poincaré映射Fig.10 Poincaré maps

4 结论

本文结合Archard和Weber-Banaschek公式分别研究了齿面动态磨损特性和由此引起的轮齿时变啮合刚度的动态变化，从而在齿轮传动系统的动力学方程中可以引入齿面磨损故障特性。

建立了考虑磨损的三自由度齿轮传动系统的多间隙非线性动力学方程，通过分岔图、李雅普诺夫指数谱、Poincaré映射和功率谱等定性和定量分析方法对系统的非线性特性进行了研究。通过研究发现了多间隙的齿轮动力学模型内部所蕴含的丰富非线性现象，发现以倍周期分岔为代表的常规进入混沌的途径，也发现了以交替出现的拟周期→锁相为途径的非常规途径，说明了含有磨损故障的多间隙齿轮传动系统非线性特性的复杂性和多样性。

发现了系统在拟周期运动时功率谱上的不可约频率分量之间满足频率相加法则，也发现了嵌套在拟周期运动窗口内部的三个相邻多周期运动之间满足两边的周期运动周期数之和与中间的周期运动周期数相等的规律。这都表明在齿轮传动系统非线性动力学模型也满足非线性系统的诸多普适性规律。

通过分岔图和对应的李雅普诺夫指数谱还可以发现具有［+，－，－，－，－，－］的混沌振动区间和具有［+，+，－，－，－，－］的超级混沌振动区间总共大致存在7个。而一般齿轮传动系统的工作区间选取在亚临界和超临界区间，本文研究系统非线性动态特性随系统激励频率的变化规律，能够为齿轮传动系统动态设计与动态性能优化提供依据。

本文在考虑齿面磨损对于动力学方程的影响只是考虑了对于时变啮合刚度的变化幅值的影响，而实际上齿面磨损可能还会引起齿侧间隙、齿面误差激励幅值等其它动态特性参数的变化，为此需要定量的研究齿侧间隙和齿面误差激励等随磨损的动态变化规律，今后将进行更加深入和系统的研究。

［1］李润方，王建军.齿轮系统动力学——振动、冲击、噪声［M］.北京:科学出版社，1997:1－3.

［2］Kahraman A，Singh R.Nonlinear dynamics of a geared rotorbearing system with multiple clearances［J］.Journal of Sound and Vibration，1991，144:469 －506.

［3］Kahraman A，Singh R.Interactions between time-varying mesh stiffness and clearance nonlinearities in a geared system［J］.Journal of Sound and Vibration，1991，146:135 －156.

［4］Blankenship G W，Kahraman A.Steady state forced response of a mechanical oscillator with combined parametric excitation and clearance type non-linearity［J］.Journal of Sound and Vibration，1995，185:743 －765.

［5］Theodossiades S，Natsiavas S.Non-linear dynamics of gearpair systems with periodic stiffness and backlash［J］.Journal of Sound and Vibration，2000，229:287 －310.

［6］Raghothama A，Narayanan S.Bifurcation and chaos in geared rotor bearing system by incremental harmonic balance method［J］.Journal of Sound and Vibration，1999，226:469 －492.

［7］刘梦军，沈允文，董海军.单级齿轮非线性系统吸引子的数值特性研究［J］.机械工程学报，2003，39:111－116.LIU Meng-jun，SHEN Yun-wen，DONG Hai-jun.Research on numerical characters of the attractors in a nonlinear gear system［J］.Journal of Mechanical Engineering，2003，39:111－116.

［8］Kahraman A，Blankenship G W.Experiments on nonlinear dynamic behaviorofan oscillatorwith clearance and periodically time-varying parameters［J］.Journal of Applied Mechanics，1997，64:217 －226.

［9］Parker R G，Vijayakar S M，Imajo T.Non-linear dynamic response of a spur gear pair:modeling and experimental comparisons［J］.Journal of Sound and Vibration，2000，237:435－455.

［10］Cai W，Chang J，Strong nonlinearity analysis for gear-bearing system under nonlinear suspension-bifurcation and chaos［J］.Nonlinear Analysis:Real World Applications，2010，11:1760－1774.

［11］Cai W，Chang J.Bifurcation and chaos analysis of spur gear pair with and without nonlinear suspension［J］.Nonlinear Analysis:Real World Applications，2011，12:979 －989.

［12］Flodin A，Andersson S.Simulation of mild wear in spur gears［J］.Wear，1997，207:16 －23.

［13］Kuang J H，Lin A D.The effect of tooth wear on the vibration spectrum of a spur gear pair［J］.Journal of Sound and Vibration ，2001，123:311 －317.

［14］Wolf A，Swift J B，Swinney H L.Determining lyapunov exponents from a time series［J］.Physica，1985，16:285－317.

［15］Eckmann J P.Roads to turbulence in dissipative dynamics system［J］.Rev Mod Phys，1981，53:643 －649.

［16］Pivka L，Zheleznyak A L，Chua L O.Arnold's tongue，Devil's staircase，and self-similarity in the driven Chua＇s circuit［J］.International Journal of Bifurcation and Chaos，1994，4:1743 1753.

［17］日本机械学会.齿轮强度设计资料［M］.北京:机械工业出版社，1984:30－32.