单孔爆破振动监测与衰减规律多元线性化回归

胡建华，尚俊龙，罗先伟，周科平

(1.中南大学 资源与安全工程学院，长沙 410083;2.湖南省深部资源开发与灾害控制重点实验室，长沙 410083;3.广西华锡集团 铜坑矿，柳州 545000)

炸药爆炸最大的特点就是能够在极短的时间内释放大量的能量，从而使得爆破被广泛应用于矿山、道路、水利及国防等国家经济建设中。但由于爆破工程环境复杂多变，爆破理论尚不成熟完备，爆破设计不完善及爆破施工中控制措施不到位等因素的存在，导致爆破作业带来一定的负面影响，如爆破作业时产生的地震波会将能量携带至周围已有工程，会引起工程振动，改变周边工程内部应力场，影响工程稳定性，最终可能导致工程失稳坍塌及工作人员伤亡等事故［1］。因此，准确预测爆破振动规律，控制爆破的灾害影响，就成为爆破工程重要内容之一。

多年来，爆破振动的预测研究工作备受国内外专家学者关注。研究方法通常分为两大类，一类是基于爆破振动波形的振动效应预测，另一类是预测爆破振动强度。范磊等［2］在分析了我国爆破振动破坏评估标准单参数局限性的基础上，提出了基于反应谱理论的爆破振动破坏效应;史秀志等［3］基于爆破振动波形，利用双线性变换的二次型方法研究了爆破振动信号时频特征，得到了可靠度更高的爆破振动波形信号时频表示法;凌同华等［4］通过对爆破振动波形信号密度曲线积分值和爆破振动三要素(振动幅值、频率和持时)进行关联分析，建立了基于波形信号密度曲线积分值爆破振动损伤安全判据;Dhakal等［5］通过数值方法，分析了爆破振动瞬时性、高频性等因素对周围结构物强度的影响，认为高惯性剪切力的存在是建筑物破坏的主要原因;张世雄等［6］基于地下矿山回采爆破振动测试结果，分析了爆破对地下建构筑物强度的影响因素，获得了爆破振速与最大单项药量和爆心距的关系;Adhikari等［7］针对露天矿大爆破和岩石边坡工程特点，根据极限平衡理论，建立了考虑矿山爆破振动扰动的边坡稳定性数学模型，对矿山边坡角进行了评价，实际应用验证了其科学合理性;Moore等［8］对砖镶面结构在不同爆破振速下的损伤效应进行了现场监测，研究了不同爆破振动速度下结构物破坏的动态应变量，提出了基于动态应变量的爆破振动对结构物强度的劣化效应。

在爆破振动波传播过程中会伴随着能量的传递，同时振动波也会因传播距离增加及岩体内部裂隙等复杂结构的影响而衰减［6］。目前关于爆破振动衰减规律研究大致可以分为4类:萨道夫斯基法［9］、数据拟合法［10］、数值法［11］和波动法［12］。萨道夫斯基公式(1)给出了质点振速、药量及爆心距之间的定量关系，并且物理意义明确，应用快捷方便，目前仍被广泛运用于爆破振动衰减分析。

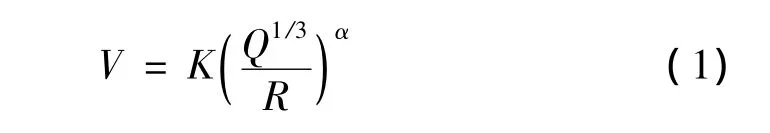
工程实践与研究表明研究表明［13］，式(1)在分析爆破振动衰减规律时考虑了单响药量Q、质点振动速度V、测点到爆心水平距离R及传播介质条件K、α等关键因素。然而，测点距爆心高程差和爆破振动主频等其他因素也会影响爆破振动效应。同时，爆破振动效应与振速之间存在着十分强的非线性关系，获取非线性回归问题解析解十分困难，因此，有必要对公式(1)进行相应的修正，增加预测爆破振动衰减规律的可靠性。

本文结合铜坑矿锌铜矿岩体井下单孔爆破漏斗试验，在现场对爆破振动进行现场监测的基础上;引入修正的萨道夫斯基爆破振动衰减公式，利用多元线性化回归法进行参量回归反演，揭示锌铜矿岩体爆破振动衰减规律，为后期矿山生产爆破设计提供指导。

1 爆破振动衰减规律多元线性化回归

1.1 修正的萨道夫斯基公式

在爆破工程中，介质质点振动速度、药量及爆心距通常被认为是表征爆破振动衰减规律的重要因素。我国《爆破安全规程》(GB6722-2003)［14］中所提到的萨道夫斯基公式定量的描述了这一点。

然而相关研究表明［13］，在绝对平整地形条件下，运用萨道夫斯基公式能够比较准确的预测爆破质点振动速度。但是工程现场地形复杂多变，质点与爆心的高差必然会影响质点振动速度，因此就增加了高差影响因子。所以为了精确预测与爆心具有一定高差的工程质点振动速度，必须引入爆心高程差影响因子β，并将式(1)修正为［15］:

式中:β为爆心高程差因子，|H|为质点与爆心高差绝对值(m)，L为质点与爆心水平距离(m)，其他符号意义同前。

1.2 振动衰减规律多元线性化回归

由式(2)可以看出，响应变量爆破振速与自变量爆破振动影响因素并不存在线性相关关系，并且影响因素不只一个，属于典型的多元非线性问题。为合理准确确定爆破振动衰减规律公式(2)中的未知参量K、α和β，对式(2)多元非线性问题进行线性化处理，并基于最小二乘法原理对未知参量K、α和β进行回归反演，具体步骤如下:

将式(2)等号两边同时取对数，使之线性化:

令x1=β，则式(3)可以转化为:

设因变量η与自变量x1，x2之间满足:

式(5)即为修正的萨道夫斯基振动衰减规律多元线性化数学模型，为了求得未知参量K、α和β，只需对(x1，x2，η)作n(n＞3)次观察(本文 n=6)。n数量越多或者观察值与实际吻合度越高，参量预测结果越精确。本文通过TC-4850爆破测振仪到了与实际情况吻合度很高的六组数据，因此可以得到一个有限样本模型:

则γ的误差平方为:

式中:n代表现场爆破测振次数(本文n=6)。

即:

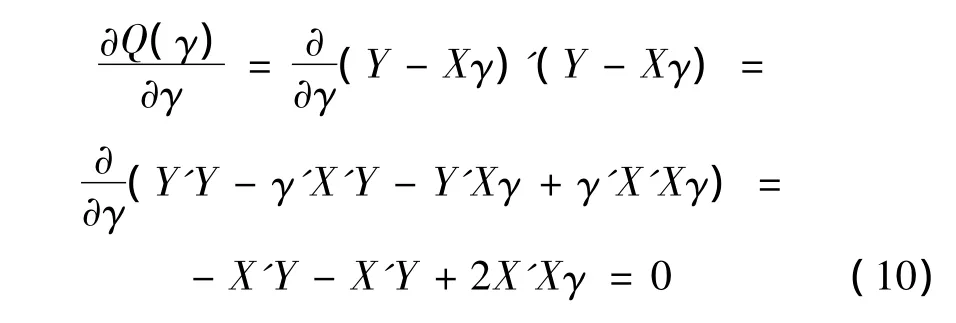
最终通过变量转换得到 K=eγ0，α =γ1，β =γ2。

故修正萨道夫斯基爆破振动衰减多元线性化回归公式为:

2 工程概况与爆破振动监测

2.1 工程概况

广西华锡集团铜坑矿是我国大型的地下矿山，年产量已超过2×106t，为保障矿山的持续稳定生产，目前正在规划低品位缓倾斜多层薄矿体的锌铜矿体。为了解锌铜矿体爆破特性，准确预测爆破振动衰减规律，指导锌铜矿体的采矿爆破设计，开展了井下爆破漏斗试验和单孔爆破振动监测分析。

2.2 爆破振动测试系统

振动监测采用TC-4850爆破振动测试仪，如图1。通过三矢量一体化分离式振动传感器接收爆破振动信息，并将所采集到的振动信息传输至TC-4850监测主机，由专用测试分析软件Blasting Vibration Analysis对振动信息进行分析，测试系统见图2。

因为爆破振动能随着距离的增加而衰减，因此尽量将测振仪布置在离爆心较近的测点进行测试。为降低爆破所产生的冲击波和飞石对监测仪器的损伤机率，根据爆破作业现场实际情况，将测振仪布置在距1号孔8 m左右的凹面位置，测点试验点的平面布置与测振仪安装状态见图3。为保证测振过程连续高效化及采集数据的完整性，设定仪器采集时间间隔略小于单孔间的微差时间。

图1 TC-4850爆破测振仪Fig.1 TC-4850 blasting vibration meter

图2 TC-4850测振系统示意图Fig.2 Sketch of the TC-4850

图3 爆破振动测试平面位置图Fig.3 Plane arrangement chart of blast

2.3 振动监测结果

通过对锌铜矿岩体爆破漏斗试验有效单孔爆破振动测试，获得六组能够体现锌铜矿岩体爆破特性的振动数据。监测得到的典型振动波形图见图4，爆破参数与振动速度监测结果见表1。

表1 爆破参数与测振仪监测结果Tab.1 The blasting parameters and monitoring results

图4 典型爆破振动波形Fig.4 Typical blasting vibration waveform

3 应用分析

利用爆破振动衰减规律多元线性化回归法，结合表1中爆破参数和振动监测数据。通过计算分析可得:

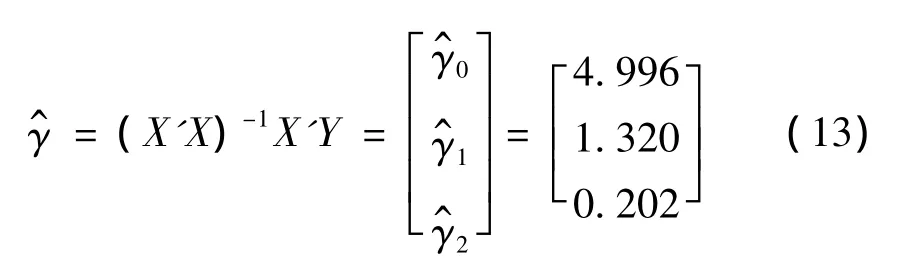
爆破振动衰减规律模型的空间形态特征如图5所示。为了验证式(15)可靠度，分别对多元回归模型(14)进行有效性检验和回归系数显著性检验。

因为 F0.05(2，3)=9.55，F0.05(1，3)=10.13 并且|F|=29 ＞9.55，F1=52.48 ＞ 10.13，F2=12.36 ＞10.13，因此式(14)线性回归显著，且回归系数 γ1和 γ2都显著不为0。表明通过上述步骤推导得到的锌铜矿爆破振动衰减公式(15)可靠性高。

同时可得到回归参数值 K=e4.996=147.744，α = γ1=1.320，β = γ2=0.202，因此锌铜矿体爆破振动衰减规律为:

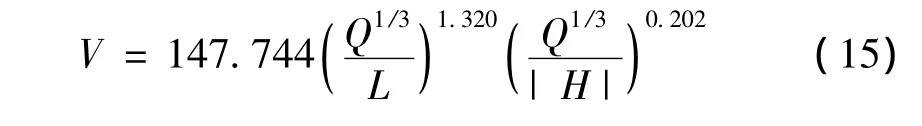
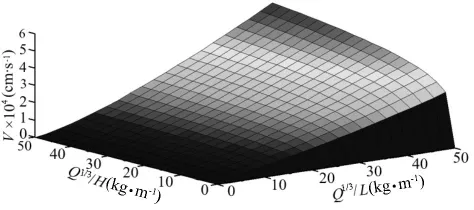
图5 锌铜矿爆破振动衰减规律空间展布Fig.5 Space configuration of attenuation law of blasting vibration in zinc-copper deposit

同时，利用传统萨道夫斯基公式(1)计算得到公式中参量 K=301.411，α=1.526。依据《爆破安全规程》(GB6722-2003)，两个参数分别落在软岩和硬岩范围内，与实际不符;相比而言，本文得到的修正公式(15)中K与α值均落在坚硬岩石范围内，这与锌铜矿岩体比较坚硬的性质相吻合，证明了式(15)的科学性与合理性，表明本文修正公式(15)更具有应用价值。

4 结论

基于地下金属矿山井下爆破漏斗试验，对单孔爆破振动进行了监测，利用测振仪分析软件Blasting Vibration Analysis对监测信息进行初步分析，获得了振动速度等表征矿岩体爆破振动传播特性的相关参量;引入考虑爆心高程差的萨道夫斯基修正公式。提出了爆破振动衰减规律的多元线性化回归模型，并基于最小二乘法原理，对模型中未知参量K、α和β进行回归分析，最终得到了修正的萨道夫斯基爆破振动衰减规律公式。并通过工程实例对所建立的爆破振动衰减规律修正公式进行了验证，主要得到了以下几点结论:

(1)我国现行的《爆破安全规程》(GB6722-2003)中所提到的萨道夫斯基公式虽然充分考虑了爆破药量、爆心距和传播介质条件对爆破振动效应的影响，但忽视了测点与爆心高程差等客观因素对振动效应的影响。因此，现行的被广泛应用的萨道夫斯基公式存在不完善之处;

(2)考虑高程差修正的萨道夫斯基爆破振动衰减规律与其影响因素之间存在复杂的非线性关系，可以采用本文所提出多元线性化回归方法将这种复杂的非线性问题线性化，进而能够容易地得到爆破振动衰减规律解析解;

(3)对于具体工程而言，其爆破振动衰减规律是客观存在的。在爆破振动监测数据可靠的前提下，有限组监测数据(n＞3)能够反应爆破振动衰减规律。锌铜矿体爆破振动衰减规律的建立是在现场监测得到的六组单孔爆破振动数据的基础上完成的，爆破振动规律的有效性检验和工程实际应用均验证了其科学合理性;

(4)爆破振动衰减规律对于爆破作业安全来说至关重要。通常情况下，实际工程一次爆破药量Q、周边某构筑物距爆破点距离L和该构筑物与爆心高差绝对值|H|可以事先得到，通过公式(15)即可得到该次爆破对周边某工程产生的振动速度，通过参考爆破安全规程中规定的不同种类构筑物的极限承载振速，即可判断该次爆破是否对周边某构筑物产生影响，从而达到防振的目的，同时也可以指导爆破设计。因此，本文所开展的研究工作能够为锌铜矿生产爆破设计提供指导，同时也进一步促进了爆破振动相关研究领域的发展。

［1］中国生，房营光，徐国元.基于小波变换的建(构)筑物爆破振动效应评估研究［J］.振动与冲击，2008，27(4):121-129.ZHONG Guo-sheng， FANG Ying-guang， XU Guo-yuan.Research on the evalucation of blasting virbation effect of structure based on wavelet transform［J］.Journal of Vibration and Shock，2008，27(4):121-129.

［2］范 磊，龙 源，郭 涛，等.基于反应谱理论的爆破振动破坏评标准分析［J］.爆破，2010，27(1):5-10.FAN Lei，LONG Yuan，GUO Tao，et al.Harm evaluation standard analysis of blasting vibration based on response spectrum theory［J］.Blasting，2010，27(1):5-10.

［3］史秀志，薛剑光，陈寿如.爆破振动信号双线性变换的二次型时频分析［J］.振动与冲击，2008，27(12):131-134.SHI Xiu-zhi，XUE Jian-guang，CHEN Shou-ru.Quadratic time-frequency distribution analysis of blasting vibration signal based on bilinear transformation［J］.Journal of Vibration and Shock，2008，27(12):131-134.

［4］凌同华，李夕兵，陈文胜.基于小波分析的爆破地震效应评估［J］.振动与冲击，2007，26(2):124-127.LING Tong-hua，LI Xi-bing，CHEN Wen-sheng.Evaluation og blast seismic effect based on wavelet analysis［J］.Journal of Vibration and Shock，2007，26(2):124-127.

［5］Dhakal R P，Pan T C.Response characteristics of structures subjected to blasting-induced ground motion ［J］.International Journal of Impact Engineering，2003，28(25):813-823.

［6］张世雄，胡建华，阳生权，等.地下工程爆破振动监测与分析［J］.爆破，2001，18(2):49-52.ZHANG Shi-xiong，HU Jian-hua，YANG Sheng-quan，et al.Monitoring and analysis of blasting vibration in underground engineering［J］.Blasting，2001，18(2):49-52.Chinese Journal of Rock Mechanics and Engineering，2003，22(11):1929-1930.

［7］Adhikari G R，Singh R B，Gupta R N.Structural response to ground vibration due to blasting in opencast coal mines［J］.Mines，Metal＆ Fueal，1989(4):135-138.

［8］Moore A J，Richards A B，Gad E.Structural response of brick veneer houses to blast vibration［C］//.Proceedings of the 29th Annual Conference on Explosives and Blasting Technique，USA，2003.

［9］言志信，言 浬，江 平，等.爆破振动峰值速度预报方法探讨［J］.振动与冲击，2010，29(5):179-182.YAN Zhi-xin， YAN Li， JIANG Ping， et al. Prediction methods for blasting-induced ground vibration velocity［J］.Journal of Vibration and Shock，2010，29(5):179-182.

［10］吕 涛，石永强，黄 诚，等.非线性回归发求解爆破振动速度衰减公式参数［J］.岩土力学，2007，28(9):1871-1878.LÜ Tao，SHI Yong-qiang，HUANG Cheng，et al.Study on attenuation parameters of blasting vibration by nonlinear regression analysis ［J］.Rock and Soil Mechanics，2007，28(9):1871-1878.

［11］唐 海，李海波，周青春，等.凹形地貌对爆破振动波传播影响的数值模拟［J］.岩土力学，2008，29(6):1540-1544.TNAG Hai，LI Hai-bo，ZHOU Qing-chun，et al.Numercial simulation of influence of concave lanform on blasting cibration wave propagation ［J］.Rock and Soil Mechanics，2008，29(6):1540-1544.

［12］谢全民，龙 源，钟明寿.小波与分形组合分析技术在爆破振动信号分析中的应用［J］.振动与冲击，2011，30(12):120-124.XIE Quan-min，LONG Yuan，ZHONG Ming-shou.Blasting vibration signal analysis with wavelet and fractal porfolio analysis technique ［J］.Journal of Vibration and Shock，2011，30(12):120-124.

［13］胡 刚，吴云龙.爆破地震振动控制的一种方法［J］.煤炭技术，2004，23(4):104-105.HU Gang，Wu Yun-long.A new method of the control of the earthquake virbation caused by explosive ［J］. Coal Technology，2004，23(4):104-105.

［14］爆破安全规程(GB6722-2003)［S］.北京:中国标准出版社，2004.

［15］谢全敏，夏元友，李新平.龙滩水电站蠕变体边坡的爆破振动控制研究［J］.岩石力学与工程学报，2003，22(11):1929-1930.XIE Quan-min，XIA Yuan-you，LI Xin-ping.Study on blasting vibration creep mass slop of longtan hydropower station［J］. Chinese JournalofRock Mechanicsand Engineering，2003，22(11):1929-1930.