基于谱聚类下采样失衡数据下SVM 故障检测
2013-09-15陶新民张冬雪郝思媛
陶新民,张冬雪,郝思媛,徐 鹏
(哈尔滨工程大学 信息与通信工程学院,哈尔滨 150001)
机械设备的状态监测和故障诊断本质上是一个模式识别的过程,其包括故障特征信息提取和状态识别两部分[1]。在状态识别阶段,由于传统的神经网络方法需要大量的典型故障样本来训练,从而使其应用受到制约。支持向量机(Support Vector Machines,SVM)是在统计学习理论基础上发展起来的一种新的机器学习方法,它在解决模式识别的小样本问题时表现出了优良性能,因此越来越受到研究人员的重视,现已广泛应用到故障检测领域[2-7]。
然而,传统SVM故障诊断方法都是基于样本均衡的前提条件下进行的。在故障检测这种特殊的应用领域,由于故障样本的收集十分困难,导致用于训练的故障样本数远远少于正常样本,这就引起了失衡数据下的故障诊断问题。传统的支持向量机对均衡数据集而言具有良好的分类能力,然而当面对失衡数据集时,分类面就会向样本数量较少的一类移动,从而使支持向量机过拟合样本点数目多的一类,而低估样本点数目少的一类,最终导致算法的故障漏检率增大。除了故障诊断,失衡数据也大量存在于其他领域,如网络入侵、信用卡欺诈检测、医疗检测、文本分类和信息检索等,因此如何提高失衡数据下SVM算法的分类性能一直是众多学者关注的重点。
针对失衡数据分类问题,学者们相继提出了多种改进算法。其中文献[9]通过SMOTE[10]对数据上采样的预处理技术实现训练数据的均衡,然而由于训练样本的增加可能会使决策域减小,导致算法过度拟合。同时,人为增加样本有可能导致噪声点增加,从而降低分类精度。下采样算法则是一个与上采样相反的方法,它通过减少多数类样本的方式来实现数据的均衡。其中包括随机下采样[11],以及借鉴实例简约的 CNN(Condensed Nearest Neighbor)算法[12],但是由于下采样算法只随机选取了多数类的一个子集,而被选取出来的子集对改善SVM分类界面是否有效却未知,如选择不当可能会导致分类效果很不理想[13-15]。因此,如何在保证数据均衡的同时,能让保存的样本信息对决策界面的生成更有效,成为利用下采样提高失衡数据下SVM算法分类性能的关键。
鉴于此,本文提出一种基于谱聚类[16]的下采样算法,首先在核空间中对正常样本进行聚类,然后根据聚类结果选择具有代表性的正常样本子集。在样本选择时根据与故障样本间的距离比例进行选择,从而实现故障样本和正常样本之间的数据均衡。试验中将本文算法应用在轴承故障诊断领域,并同其他算法进行了比较,实验结果表明本文建议的算法在数据失衡情况下分类性能较其他算法有较大幅度提高。
1 支持向量机(SVM)
支持向量机是由Vapnik等提出的一类新型的机器学习算法。它是建立在统计学习理论和结构风险最小化原则之上,通过固定经验风险,最小化置信风险,将输入空间映射到高维内积空间,有效避免了“维数灾难”。在解决小样本集、非线性高维数模式识别问题上具有很大优势,并在故障诊断领域受到普遍关注。
以两类训练样本集为例,设给定的训练样本集为{(x1,y1),(x2,y2),…,(xn,yn)},yi∈{+1,- 1},i=1,2,…,n代表样本类别,核函数为K。构造代价函数使其最小:
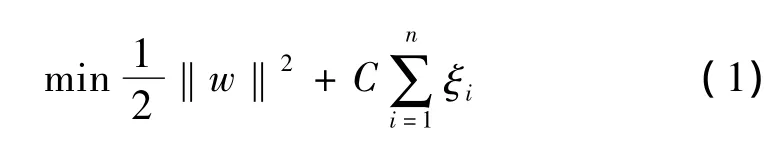
约束条件是:

其中:ξi是松弛变量,表示训练样本的错分程度,C是惩罚常数,控制对错分样本的惩罚程度,w和b分别为判决函数f(x)=(w·x)+b的权向量和阈值。拉格朗日函数为:

其中:αi和βi是拉格朗日算子。根据KKT条件:

αi>0的样本是支持向量。判别函数为:

2 基于谱聚类下采样失衡数据SVM算法
2.1 基于谱聚类的下采样(SC-Under sampling)
由于多数类和少数类样本数目失衡,分布在SVM分类界面附近的样本比例也不相同,从而导致多数类样本成为支持向量的概率远远大于少数类样本。由式(6)可知,算法最终学习得到的分类界面就会向少数类样本移动,这样势必会导致SVM分类器对小数量样本类别产生较大的测试误差。因此,为了提高SVM分类器的分类性能,必须解决SVM算法在失衡数据情况下分类边界向少数类样本偏移的问题。
在处理失衡样本的问题中,目前的下采样算法只是将远离边界的样本进行了删除,或者随机选取多数类的一个子集,没能考虑采样后子集的信息是否有效。这种方法虽然能实现训练样本数目间的均衡,但对改善SVM的分类界面没有任何影响,这是由于SVM算法分类界面的形成只与支持向量有关。因此,为了能有效改善SVM分类界面的位置,使其向多数类样本方向偏移,就需要删除部分边界样本,为了不改变多数类样本集合空间结构,本文利用聚类算法对多数类样本聚类,然后选择那些聚类中具有局部空间代表意义的样本作为新的训练样本,如此即可实现对多数类样本集合进行有目的地筛选。
在聚类算法的选择上,我们选择谱聚类算法(Spectral Clustering Algorithm)。该算法首先根据给定的样本数据集定义一个描述成对数据点相似度的亲合矩阵,并计算矩阵的特征值和特征向量,最后选择合适的特征向量聚类不同的数据点。由于这种算法不用对数据的全局结构作假设,并且具有识别非凸分布聚类的能力,因此非常适合于许多实际问题中。另外,谱聚类算法能在核空间聚类,这使其能与SVM算法实现无缝连接。下面简介一下谱聚类算法:
定义一个无方向图G=(V,E),其中定点集合V={v1,v2,…,vn},n是样本个数,假设 G 是个加权图,它的两个定点vi和vj的边由wij>0表示。进一步定义该图的加权连接矩阵为W=(wij),i,j=1,…,n。如果wij=0则表示vi和vj顶点间没有边。由于G是个无向图,因此wij=wji。其中顶点vi⊂V的度及图的度矩阵分别定义为:

对应该图的标准化图拉普拉斯矩阵定义为:谱聚类具体算法描述如下:
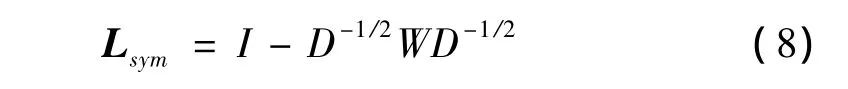
输入:相似矩阵S∈Rn×n,聚类个数k
(1)根据相似矩阵构造无方向相似图G=(V,E),
其中W作为它的加权连接矩阵;
(2)计算标准化图拉普拉斯矩阵Lsym;
(3)计算拉普拉斯矩阵Lsym的前k个特征矢量μ1,μ2,…,μk;
(4)将 μ1,μ2,…,μk作为列生成 U∈Rn×k;
(5)通过对U矩阵中的每一行进行标准化处理tij生成 T∈Rn×k;
(6)对于每一行 i=1,2,…,n,ti∈Rk作为 T 矩阵的第i行的向量;
(7)对(ti)i=1,2,…,n利用K-means算法进行聚类形成 C1,C2,…,Ck;
2.2 基于谱聚类下采样失衡数据SVM算法
将利用上述基于谱聚类的下采样算法对多数类样本进行预处理,然后将采样后的多数类样本子集同全部少数类样本共同组合成新的训练样本集,输入到SVM算法中进行训练学习。具体步骤如下:
(1)设置预采样的多数类样本点个数MajorN=m*MinorN;m为两者数量上的比例;
(2)算法首先利用多数类样本集合建立一个基于高斯核的相似矩阵S∈Rn×n,n是原有多数类样本的个数;
(3)然后利用上述的谱聚类算法对多数类样本进行聚类分析生成聚类 A1,…,Ak,k=MajorN;
(4)选择每一个聚类中具有代表性的样本点,其中在每一个聚类中样本选择数取决于该聚类的大小以及该聚类中的样本与少数类样本点的平均距离的大小,聚类越大,则选择的样本数就越多;离少数类样本越近则选择的越少,如此选择是为了有目的地删除多数类中的边界样本信息点。具体公式如下:

其中:Ksizei为聚类Ai的大小,IDisti为聚类Ai到少数类的平均距离,是每一个聚类中选择的样本个数;
(6)将采样得到的多数类训练样本子集和全部的少数类样本组合作为新的训练样本,输入到SVM算法中进行训练学习,其中核参数与相似矩阵S的核参数相同,即谱聚类和 SVM分类算法都在一个空间中进行;
(7)最后,根据训练得到的分类界面进行新样本的类别辨识。
图1是在失衡比例为100∶1时SVM分类情况。其中十字型为多数类样本,圆圈为少数类样本,而被圈起来的十字为支持向量。我们清楚地看到SVM分类边界向着少数类方向进行了偏移。而图2为m=5时谱聚类下采样失衡数据下SVM算法的分类界面情况,其中正方形点为多数类到少数类的最远点;六角形为多数类到少数类的中心点;倒三角形为多数类到少数类的最近点,不难看出通过处理后的SVM的分类性能得到了改善,分类边界向着多数类方向偏移。

图1 数据样本比例为100∶1时SVM算法的分类边界Fig.1 Classification boundary of SVM under the proportion 100∶1

图2 谱聚类下采样后SVM算法分类边界的变化Fig.2 The classification boundary of the spectral clustering under-sampling SVM
2.4 失衡数据下算法性能评测方法
以往适用于均衡数据分类的以整体分类错误为目标的性能评估指标,已不再适合失衡数据集分类。由于传统的性能评估是从整体分类器考虑的,以此为指导训练学习得到的失衡数据分类器容易将少数类样本错分。这是因为少数类样本数目所占比例不大,将其分错对总体的分类性能指标的影响并不大。针对传统性能指标存在的缺陷,近年来很多学者提出一些用于失衡数据分类的性能评测指标,常见的有以下几种:

表1 混合矩阵Tab.1 Hybrid matrix
首先定义在失衡数据集中少数类(正类)为P,多数类(负类)为N;FP是指将多数类样本错分成少数类的数目,而FN是指将少数类样本错分成多数类的数目,同理TP和TN分别表示少数类和多数类样本被正确分类的个数。由此可以得到:
少数类样本查全率:
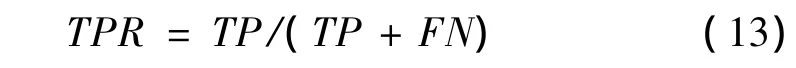
多数类样本查全率:

少数类样本查准率:

多数类样本错分率:

几何平均正确率G-mean:

少数类的F-measure:

性能指标G综合考虑了少数类和多数类两类样本的分类性能,如果分类器分类偏向于其中一类会影响另一类的分类正确率,从而G值会很小。性能指标F则考虑少数类样本的查全率和查准率的相结合,其中任何一个值都能影响F值的大小,所以它能综合地体现出分类器对少数类的分类效果。
3 试验分析
3.1 评测数据
为了展示样本数据集失衡时对传统支持向量机算法分类性能的影响以及本文提出的算法在失衡数据情况下的分类能力,采用来自美国Case Western Reserve University电气工程实验室的实验数据[14]。该振动信号的收集来自于安装在感应电机输出轴支撑轴承上端机壳上的振动加速度传感器。实验模拟了滚动轴承的4种运行状态:① 正常运行状态;② 外圈故障;③ 内圈故障;④ 滚动体故障。
近年来,基于相空间重构(RPS)模式的故障诊断方法得到了广泛应用,为此本文选用训练样本易得的正常样本相空间的投影系数作为故障特征。即首先确定正常样本相空间的参数,然后取其他类型的样本在该空间的投影系数作为故障诊断的特征[1],具体描述如下:
若轴承振动信号时间序列为:y1,y2,y3,…,yn(yi∈ R)当正常样本相空间的嵌入维数为m,延迟时间间隔为τ,则采用时间延迟技术重构相空间为:

式中:xi为信号在重构相空间的投影系数,其中相空间的参数利用互信息函数指标来确定,嵌入维度选择文献[1]提供的方法。试验确定的正常样本相空间的延迟间隔τ等于2,嵌入维度m等于5,因此故障诊断的特征为5维矢量。最终形成正常样本、内圈故障样本、外圈故障样本和滚动体故障样本四种5维矢量作为故障检测特征。
3.2 故障检测试验对比
本文选择1 000个正常样本、1 000个内圈故障样本、1 000个外圈故障样本和1 000个滚动体故障样本组成训练集,同样分别选择10 000个样本组成测试样本集合。为了测试本文算法在数据失衡情况下的分类性能,实验中取失衡比例分别为 100∶1、50∶1、40∶1、30∶1、20∶1、10∶1 的内圈、外圈以及滚动体故障样本点进行试验。将本文基于谱聚类下采样失衡SVM算法(SC-SVM)同基于SVM算法、基于随机下采样SVM算法(RU-SVM)、基于CNN下采样SVM算法和基于SMOTE过采样SVM算法的试验结果进行比较。试验中SVM核函数为高斯核函数,核宽度为10。惩罚因子C=10。SMOTE算法中的 K值为6。将F-measure、G-mean作为性能测评指标。其中图3、图4为内圈故障检测结果,图5、图6为外圈故障检测结果,图7、图8为滚动体故障检测结果,图中各类算法分别为SCSVM(基于谱聚类下采样支持向量机)、SVM(传统支持向量机)、RUSVM(随机下采样支持向量机)、CNNSVM(简明最近邻支持向量机)、SMOTESVM(少数类上采样算法支持向量机)。
从试验结果可以看出,随着失衡比例系数的增大,各种算法的分类性能都在逐渐下降,但本文算法仍优于其他算法,原因在于本文算法充分结合了SVM算法的特点,利用谱聚类在核空间对样本进行聚类,并且有目的的选择多数类样本点进行下采样,同时还与SVM算法无缝连接,使得本文算法的失衡数据分类性能优于其他算法。从试验结果可知,传统SVM算法在样本失衡时少数类样本错分率达到100%,分类性能极其不理想。而随机下采样算法由于去除样本随机,可能会导致有效样本被删除,因此分类效果也很不理想。CNN算法由于是通过将远离分类边界的多数类样本进行删除的方式来实现样本均衡,而在SVM算法中,决定分类边界位置的都是边界样本,因此该算法虽然实现了数据均衡,但分类边界并没有发生改变,分类效果同样也不理想。而SMOTE上采样算法本身对数据十分依赖,即要求少数样本集合是凸集,所以当少数类样本缺乏代表性时,分类效果就会受到了很大影响。

图3 不同比例失衡内圈故障数据下F-measure性能比较Fig.3 Comparison of F-measure performance between different proportions of imbalanced datas under inner faults

图4 不同比例失衡内圈故障数据下G-mean性能比较Fig.4 Comparison of G-mean performance between different proportions of imbalanced datas under inner fault

图5 不同比例失衡外圈故障数据下F-measure性能比较Fig.5 Comparison of F-measure performance between different proportions of imbalanced datas under outer faults
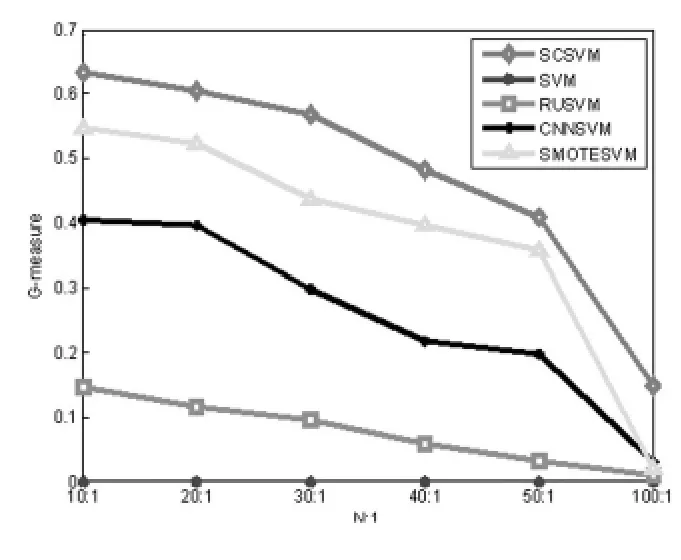
图6 不同比例失衡外圈故障数据下G-mean性能比较Fig.6 Comparison of G-mean performance between different proportions of imbalanced datas under outer faults

图7 不同比例失衡滚动体故障数据下F-measure性能比较Fig.7 Comparison of F-measure performance between different proportions of imbalanced datas under ball faults

图8 不同比例失衡滚动体故障数据下G-mean性能比较Fig.8 Comparison of G-mean performance between different proportions of imbalanced datas under ball faults
3.3 高斯核半径的参数对SVM性能的影响
为了验证高斯核半径参数对本文算法性能的影响,试验中选内圈故障样本、外圈故障样本、滚动体故障样本来进行,其中正常样本与故障样本比例为50∶1,选取不同高斯核参数值观察F-measure和G-mean的性能变化,试验结果如图9~10所示。当高斯核半径很小时,由于分类器过度依赖训练样本,因此出现了过拟合现象,分类效果不好。随着高斯核参数的增大,算法的性能逐渐提高,而当参数值达到一定程度,分类器的学习能力开始逐渐变差,错分率也随之增大,这是由于本文算法是下采样算法,所选取的样本都具有一定的代表性,因此希望SVM应具备一定的学习能力。因此结合试验结果可知,当核宽度选取为0.8~13时本文算法的分类性能最佳。
3.4 支持向量数量的对比试验
为了比较算法之间的效率,本文利用训练后的支持向量的个数作为评测标准,这是由于SVM分类算法的决策函数只与支持向量有关,因此计算量也同样与其个数有关系。在该试验中,本文选择1 000个正常样本、1 000个内圈故障样本、1 000个外圈故障样本和1 000个滚动体故障样本组成训练集,同样分别选择10 000个样本组成测试样本集合。本文将正常样本与故障样本比例定于50∶1,对内圈故障样本、外圈故障样本和滚动体故障样本的支持向量数目进行了统计,试验结果如表2。从试验结果可知,虽然随机下采样算法支持向量个数略少于本文算法,但是分类效果却远远低于本文算法。而上采样算法支持向量的个数则是本文算法的百倍以上,计算量很大,根本无法满足故障诊断领域实时检测的需要,因此可以说在综合考虑算法分类性能同检测与训练时间方面,本文算法要优于其他算法。

图9 不同Sigma下F-measure值Fig.9 F-measure value under different Sigma

图10 不同sigma下G-mean值Fig.10 G-mean value under different Sigma

表2 不同算法的支持向量数量对比Tab.2 Comparison of the number of support vectors between different algorithms
4 结论
本文针对传统支持向量机算法在解决故障检测问题时,由于失衡数据的影响导致分类性能下降的问题,提出一种基于谱聚类下采样失衡SVM故障诊断方法。试验部分将该算法与其他算法进行比较,结果表明本文算法在F-measure及G-mean性能上均优越于其他算法。试验部分也考察了核宽度的取值对算法性能的影响,结果表明当参数适当增大时会有利于提高算法的分类性能。试验最后将本文算法得到的支持向量的数目与其他算法进行比较,结果表明本文算法在提高算法分类性能的同时也大大降低了故障检测的时间。需要指出的是本文算法具有很强的推广能力,不仅适合于故障检测,也同样适用于其他失衡数据情况下的应用领域。
[1]陶新民,杜宝祥,徐 勇.基于HOS奇异值谱和SVDD的轴承故障检测方法[J].振动工程学报,2008,21(2):401-405.TAO Xin-min,DU Bao-xiang,XU Yong. Bearingfault detection using SVDD based on HOS-singular value spectrum[J].Journal of Vibration Engineerin,2008,21(2):401-405.
[2]王红军,张建民,徐小力.基于支持向量机的机械系统状态组合预测模型研究[J].振动工程学报,2006,19(2):242-245.WANG Hong-jun,ZHANG Jian-min,XU Xiao-li.Study on combination trend prediction technologyformechaninery system based on SVM[J].Journal of Vibration Engineerin,2006,19(2):242 -245.
[3]唐和生,薛松涛.序贯最小二乘支持向量机的结构系统识别[J].振动工程学报,2006,19(3):382-387.TANG He-sheng,XUE Song-tao.Sequential LS-SVM for structural systems identification[J].Journal of Vibration Engineerin,2006,19(3):382 -387.
[4]张建明,曾建武.基于粗糙集的支持向量机故障诊断[J].清华大学学报(自然科学版),2007,47(S2):1773-1777.ZHANG Jian-ming,ZENG Jian-wu.Fault diagnosis based on RS and SVM[J].Journal of Tsinghua University(Science and Technology),2007,47(S2):1773 -1777.
[5]袁胜发,褚福磊.支持向量机及其在机械故障诊断中的应用[J].振动与冲击,2007,26(11):29-34.YUAN Sheng-fa,CHU Fu-lei.Support vection machines and its application in machine fault diagnosis[J].Journal of Vibration and Shock,2007,26(11):29 -34.
[6]袁胜发,褚福磊.次序二叉树支持向量机多类故障诊断算法研究[J].振动与冲击,2009,28(3):51-54.YUAN Sheng-fa,CHU Fu-lei.Mult-iclass fault diagnosis based on support vector machines with sequenced binary tree archtecture[J].Journal of Vibration and Shock,2009,28(3):51-54.
[7]Ravikumar B,Thukaram D.Application of support vector machines for fault diagnosis in power transmission system[J].Iet Generation Transmission &Distribution,2008,2(1):119-130.
[8]Akbani R,Kwek S,Japkowicz N.Applying support vector machines to imbalanced datasets[C].Proceedings of the 2004 European Conference on Machine Learning(ECML'2004),2004:39 -50.
[9]Liu Y,An A,Huang X.Boosting prediction accuracy on imbalanced datasets with SVM ensembles[C].Proceedings of the 10th Pacific-Asia Conference on Knowledge Discovery and Data Mining(PAKDD'06),Singapore,2006:107 -118.
[10]Chawla N,Bowyer K,Hall L,et al.SMOTE:synthetic minority over-sampling technique[C]. International Conference on Knowledge Based Computer Systems,2002:321-357.
[11]Akban I R,Kwek S,Japkow I.Applying support vector machines to imbalanced datasets[C]Proc of the 15th European Conference on Machines Learning,2004:39 -50.
[12]Bastista G E,Prati R C,Monard M C.A study of the behavior of several methods for balancing machine learning training data[J].ACM SIGKDD Exploration Newsletter,2004,6(1):20-29.
[13]陶新民,徐 晶,童智靖.失衡数据下基于阴性免疫的过抽样算法[J].控制与决策,2010,25(6):867 -873.TAO Xin-min,XU Jing,TONG Zhi-jing. Over-sampling algorithm based on negative immune in imbalanced data sets learning[J],Control and Decision,2010,25(6):867 -873.
[14]Sun Y,Kamel M S,Wong A K C.Cost-sensitive boosting for classification of imbalanced data[J].Pattern Recognition,2007,40(12):3358 -3378.
[15]曾志强,吴 群,廖备水,等.一种基于核SMOTE的非平衡数据集分类方法[J].电子学报,2009,39(11):2489-2495.ZENG Zhi-qiang, WU Qun, LIAO Bei-shui, et al. A classification method for imbalance data set based on kernel SM0TE[J].Acta Electronica Sinica,,2009,39(11):2489-2495.
[16]王 玲,薄列峰,焦李成.密度敏感的半监督谱聚类[J].软件学报,2007,18(10):2412 -2422.WANG Ling,BO Lie-feng,JIAO Li-cheng.Density-sensitive semi-supervised spectral clustering[J].Journal of Software,2007,18(10):2412-2422.
