应用模糊集理论对壮肝逐瘀煎抗肝纤维化的优化研究

王振常 柳 明 黄晶晶 吕建林

广西中医药大学第一附属医院肝病科，广西南宁 530023

壮肝逐瘀煎是在已故的全国有名老中医林沛湘教授治疗慢性肝炎、肝炎肝硬化有效验方的基础上组方而成，经过多年实践其有效性不容置疑[1-4]，其经验和理论的积累可能通过数十载而得来，理论的构建是极其艰苦的，一旦建成如不能通过技术将其复制出来，推广出去，将大大降低其价值及社会贡献。现代科学具有很强的推演体系，使其可以通过以现代技术为中介进行大规模的推广应用。这里需要说明的是，现代技术是一种具有很强的复制功能和很好的可重复性的手段[5]。本研究复制四氯化碳（CCl4）复合因素大鼠肝纤维化模型，以药效模型为指标，基于模糊集理论建立药物与各功效指标的数学模型，对方中各成分进行量化控制，分析壮肝逐瘀煎中各药物的重要性，去除方中冗余成分，使组方更科学、精确。

1 材料与方法

1.1 实验动物

健康清洁SPF大鼠260只，雌雄各半，由广西医科大学动物实验中心提供，合格证号：SCXK桂2010-0010。

1.2 药物与试剂

壮肝逐瘀煎（黄芪45 g，牡蛎30 g，土鳖虫5 g，鳖甲30 g，黄精 20 g，枸杞 20 g，薏苡仁 45 g，橘红 10 g，泽兰 30 g，炒鸡内金 15 g，虎杖 20 g，大枣 15 g）由广西中医药大学第一附属医院药剂科提供，按等效剂量计算大鼠所需全方及拆方生药量，经浸泡、煎煮3次后、过滤及水浴蒸发制成每毫升含1 g生药的水煎液（浓度100%）2000 mL药液，高温灭菌后4℃冰箱保存备用。大黄蛰虫丸0.2 g/kg（广东阳江制药厂有限公司，批号Z19991101），4℃冰箱内保存备用。CCl4分析纯购自于中国医药集团上海化学试剂公司。肿瘤坏死因子 α（TNF-α）、白介素（IL）-2、IL-6、IL-10 均为武汉博士德生物工程有限公司生产。

1.3 编制因素位级表

壮肝逐瘀煎由12味药物组成，分析方中各药用药与否的差别、药物用量的差别、各药物搭配的差别，故为12因素3位级，采用列表。见表1。

1.4 动物分组

健康清洁级SPF大鼠260只，体重120～150 g，随机取15只作为正常对照组（A组）。剩余大鼠进行肝纤维化造模，于第4周末造模大鼠随机处死5只，证实肝纤维化形成后，将其余造模大鼠随机分为病理模型组（B组）、大黄蛰虫丸组（C组）、壮肝逐瘀煎配比1～28组，每组8只。

1.5 造模及给药方法

采用韩德五等[6]报道的方法复制CCl4复合因素大鼠肝纤维化模型，为了防止肝脏自然修复对实验结果造成的影响，各组于用药开始后仍每周注射40%CCl4油剂1.5 mL/kg 1次，A组除外。造模4周后各组分别予以壮肝逐瘀煎配比1～28组药液、生理盐水（A、B组），大黄蛰虫丸（C组）灌胃给药，灌胃液体量为0.1 mL/kg，1次/d，其浓度及等效剂量按体表面积折算。

1.6 标本制备

各组于用药治疗后4、8、12周，禁食12 h，随机选取5只大鼠称重，经1%戊巴比妥麻醉，股静脉采血后处死，剖取肝脏，取肝脏右叶相同部位组织1块置入10%甲醛，作常规石醋切片，将余下肝脏组织于液氮中速冻，-196℃保存，以备匀浆测羟脯氨酸（HYP）、提取mRNA及RT-PCR分析用。血清于-70℃冰箱内保存备检测。

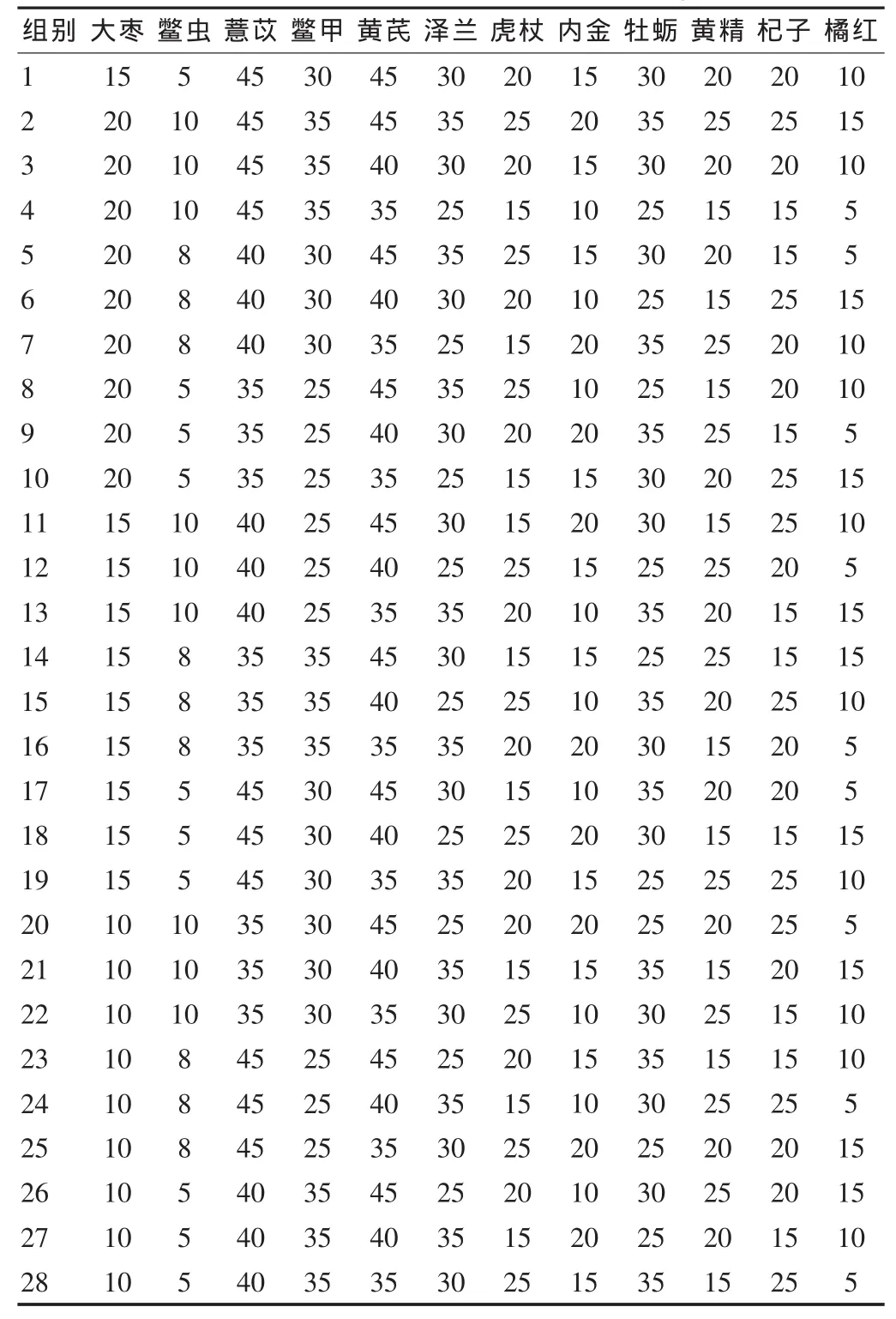
表1 1～28组壮肝逐瘀颗粒配比情况（g）

1.7 观察指标及方法

①酶联免疫吸附实验（ELISA法）测定血清IL-2、6、10及 TNF-α；②肝组织 HYP测定：李文才等[7]法依据标准曲线计算HYP含量；③大鼠肝组织过氧化物歧化酶（SOD）活性及丙二醛（MDA）含量，分别按MDA测定盒和SOD测定盒方法检测；④采用半定量RT-PCR法分析肝组织MMP-1、2、3及基质金属蛋白酶抑制物（TIMP）-1、2的mRNA表达差异。取PCR产物和 PCR Markers各 10 μL，加缓冲液，琼脂糖凝胶电泳，溴乙锭染色，紫外透射反射分析仪下观察并摄像，图像分析软件分析电泳条带条的面积和光密度，以平均值代表相应基因的表达量，并除以相应βactin的mRNA的平均值，即为MMP-1、2、3及TIMP-1、2的相对表达量。

2 结果

2.1 各组各指标水平比较

各组 IL-2、6、10、TNF-α、肝组织 HYP、SOD、MDA水平，MMP-1、2、3 及 TIMP-1、2mRNA 水平表达及肝组织炎纤维化程度比较，分别见表2～4。

表2 各组 IL-2、6、10 及 TNF-α 水平比较（pg/mL，±s）

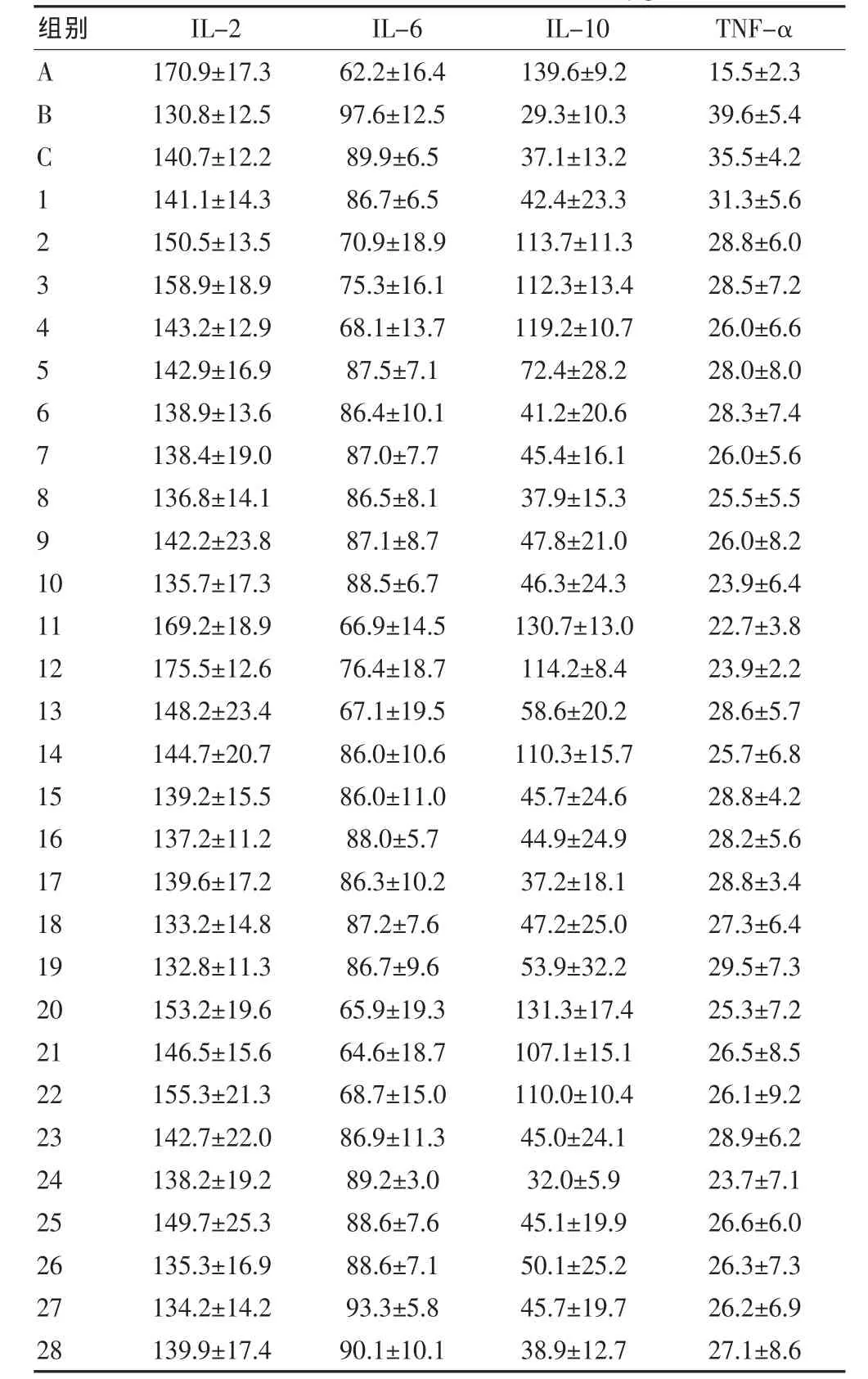
表2 各组 IL-2、6、10 及 TNF-α 水平比较（pg/mL，±s）

注：IL-2：白介素-2；IL-6：白介素-6；IL-10：白介素-10；TNF-α：肿瘤坏死因子-α

ABC1234567891 0 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 170.9±17.3 130.8±12.5 140.7±12.2 141.1±14.3 150.5±13.5 158.9±18.9 143.2±12.9 142.9±16.9 138.9±13.6 138.4±19.0 136.8±14.1 142.2±23.8 135.7±17.3 169.2±18.9 175.5±12.6 148.2±23.4 144.7±20.7 139.2±15.5 137.2±11.2 139.6±17.2 133.2±14.8 132.8±11.3 153.2±19.6 146.5±15.6 155.3±21.3 142.7±22.0 138.2±19.2 149.7±25.3 135.3±16.9 134.2±14.2 139.9±17.4 62.2±16.4 97.6±12.5 89.9±6.5 86.7±6.5 70.9±18.9 75.3±16.1 68.1±13.7 87.5±7.1 86.4±10.1 87.0±7.7 86.5±8.1 87.1±8.7 88.5±6.7 66.9±14.5 76.4±18.7 67.1±19.5 86.0±10.6 86.0±11.0 88.0±5.7 86.3±10.2 87.2±7.6 86.7±9.6 65.9±19.3 64.6±18.7 68.7±15.0 86.9±11.3 89.2±3.0 88.6±7.6 88.6±7.1 93.3±5.8 90.1±10.1 139.6±9.2 29.3±10.3 37.1±13.2 42.4±23.3 113.7±11.3 112.3±13.4 119.2±10.7 72.4±28.2 41.2±20.6 45.4±16.1 37.9±15.3 47.8±21.0 46.3±24.3 130.7±13.0 114.2±8.4 58.6±20.2 110.3±15.7 45.7±24.6 44.9±24.9 37.2±18.1 47.2±25.0 53.9±32.2 131.3±17.4 107.1±15.1 110.0±10.4 45.0±24.1 32.0±5.9 45.1±19.9 50.1±25.2 45.7±19.7 38.9±12.7 15.5±2.3 39.6±5.4 35.5±4.2 31.3±5.6 28.8±6.0 28.5±7.2 26.0±6.6 28.0±8.0 28.3±7.4 26.0±5.6 25.5±5.5 26.0±8.2 23.9±6.4 22.7±3.8 23.9±2.2 28.6±5.7 25.7±6.8 28.8±4.2 28.2±5.6 28.8±3.4 27.3±6.4 29.5±7.3 25.3±7.2 26.5±8.5 26.1±9.2 28.9±6.2 23.7±7.1 26.6±6.0 26.3±7.3 26.2±6.9 27.1±8.6组别 IL-2 IL-6 IL-10 TNF-α

2.2 采用模糊集理论对中药复方壮肝逐瘀煎抗肝纤维化的配伍规律进行综合评价

2.2.1 指标的标准化处理 为方便起见，用fj表示从表2开始指标依次排列位于第j位的指标j=1，2…，12。首先将实验数据写成区间数，例如表2中第1组在指标 f1（IL-2）的指标值（141.1±14.3）pg/mL 写成区间数a11=[aL11，aR11]=[126.8，155.4]；第 1 组在指标 f2（IL-6）的指标值 （86.7±6.5）pg/mL 写成区间数 a12=[a12L，a12R]=[80.2，93.2]；其余类似表达可得区间数的决策矩阵A=（aij）31×12，其中， i=A，B，0，1，2，…，28，分别表示 A、B、0、1、2、…、28 组，j=1,2…，12。 其次，12 个评价指标中有3个正向（极大型）指标和9个逆向（极小型）指标，为了消除不同物理量纲对决策结果的影响，采用如下“极差变换法”将区间数矩阵 A=（aij）31×12转化为规范化的区间数矩阵 B=（bij）31×12[2]。

①对于正向（极大型）指标 fj（j=1，3，6），记 aRj=B，0，1，2，…，28。

表3 各组肝组织HYP、SOD、MDA的比较（±s）

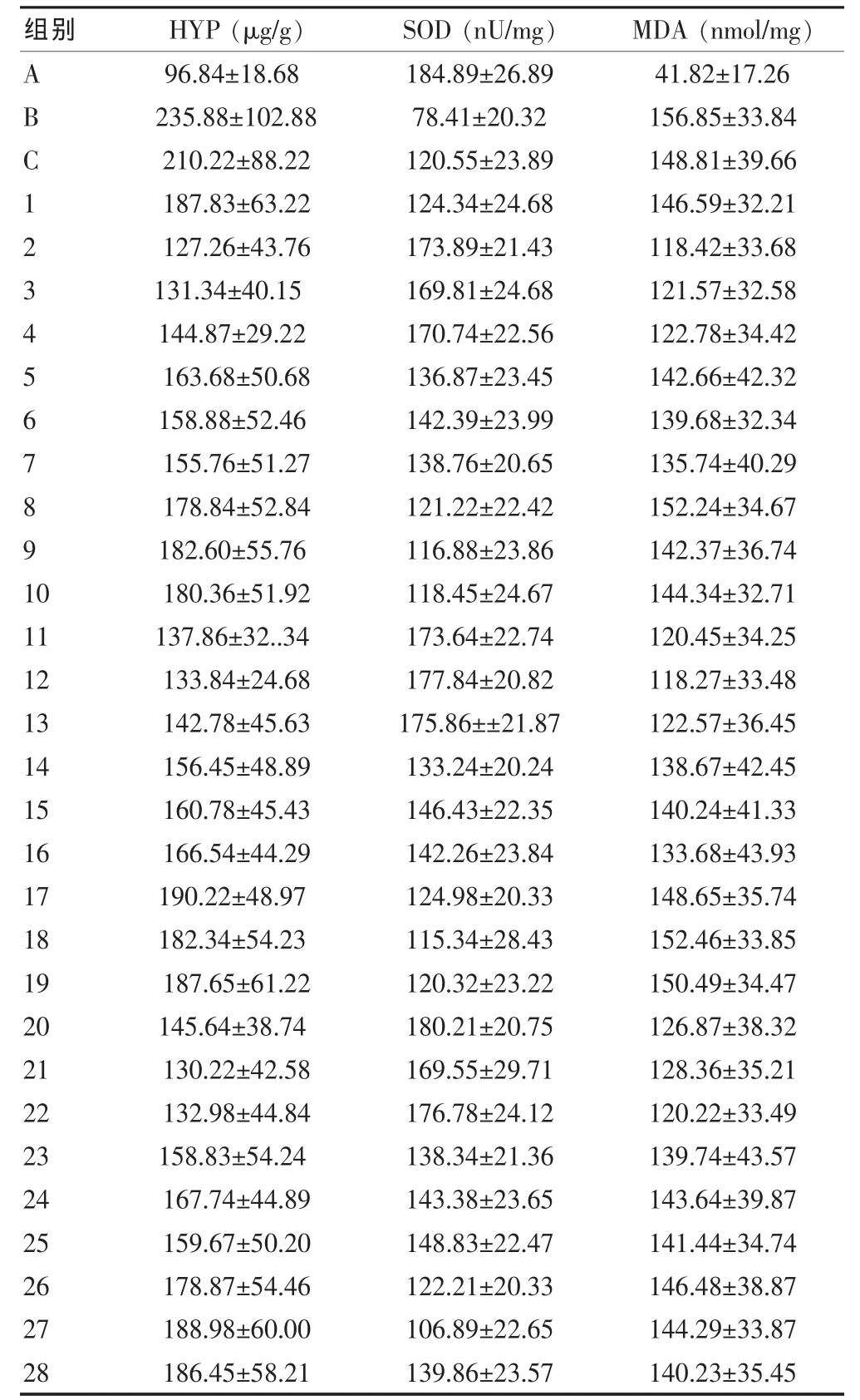
表3 各组肝组织HYP、SOD、MDA的比较（±s）

注：HYP：羟脯氨酸；SOD：过氧化物歧化酶；MDA：丙二醛

ABC1234567891 0 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 96.84±18.68 235.88±102.88 210.22±88.22 187.83±63.22 127.26±43.76 131.34±40.15 144.87±29.22 163.68±50.68 158.88±52.46 155.76±51.27 178.84±52.84 182.60±55.76 180.36±51.92 137.86±32..34 133.84±24.68 142.78±45.63 156.45±48.89 160.78±45.43 166.54±44.29 190.22±48.97 182.34±54.23 187.65±61.22 145.64±38.74 130.22±42.58 132.98±44.84 158.83±54.24 167.74±44.89 159.67±50.20 178.87±54.46 188.98±60.00 186.45±58.21 184.89±26.89 78.41±20.32 120.55±23.89 124.34±24.68 173.89±21.43 169.81±24.68 170.74±22.56 136.87±23.45 142.39±23.99 138.76±20.65 121.22±22.42 116.88±23.86 118.45±24.67 173.64±22.74 177.84±20.82 175.86±±21.87 133.24±20.24 146.43±22.35 142.26±23.84 124.98±20.33 115.34±28.43 120.32±23.22 180.21±20.75 169.55±29.71 176.78±24.12 138.34±21.36 143.38±23.65 148.83±22.47 122.21±20.33 106.89±22.65 139.86±23.57 41.82±17.26 156.85±33.84 148.81±39.66 146.59±32.21 118.42±33.68 121.57±32.58 122.78±34.42 142.66±42.32 139.68±32.34 135.74±40.29 152.24±34.67 142.37±36.74 144.34±32.71 120.45±34.25 118.27±33.48 122.57±36.45 138.67±42.45 140.24±41.33 133.68±43.93 148.65±35.74 152.46±33.85 150.49±34.47 126.87±38.32 128.36±35.21 120.22±33.49 139.74±43.57 143.64±39.87 141.44±34.74 146.48±38.87 144.29±33.87 140.23±35.45组别 HYP （μg/g） SOD （nU/mg） MDA （nmol/mg）

②对于逆向（极小型）指标：fj（j=2，3，5，7，… ，12）， 记i=A，B，0，1，2，…，28。

经过变换后所有的指标都被转化为正向 （极大型）指标，且将规范化的区间数矩阵 B=（bij）31×12。

2.2.2 评价方法 （模型）——逼近理想点法 理想点法（technique for order preference by similarity to ideal solution，TOPSIS）是一种常用的有限方案多属性决策分析法，同时也是一种有效的多指标评价方法。其基本思想是：根据指标性质以各指标的最优值组成的有序数组作为正理想点，即理想方案，以各指标的最劣值组成的有序数组作为负理想点，即负理想方案。然后计算各备选方案的各指标值所组成的有序数组到正、负理想点的距离，以及各方案与理想方案的贴近度，依据各备选方案与理想方案的贴近度来判断备选的优劣[8-9]。

表4 各组大鼠肝组织中MMP-1、MMP-2、MMP-3及 TIMP-1、2 mRNA 表达水平（±s）

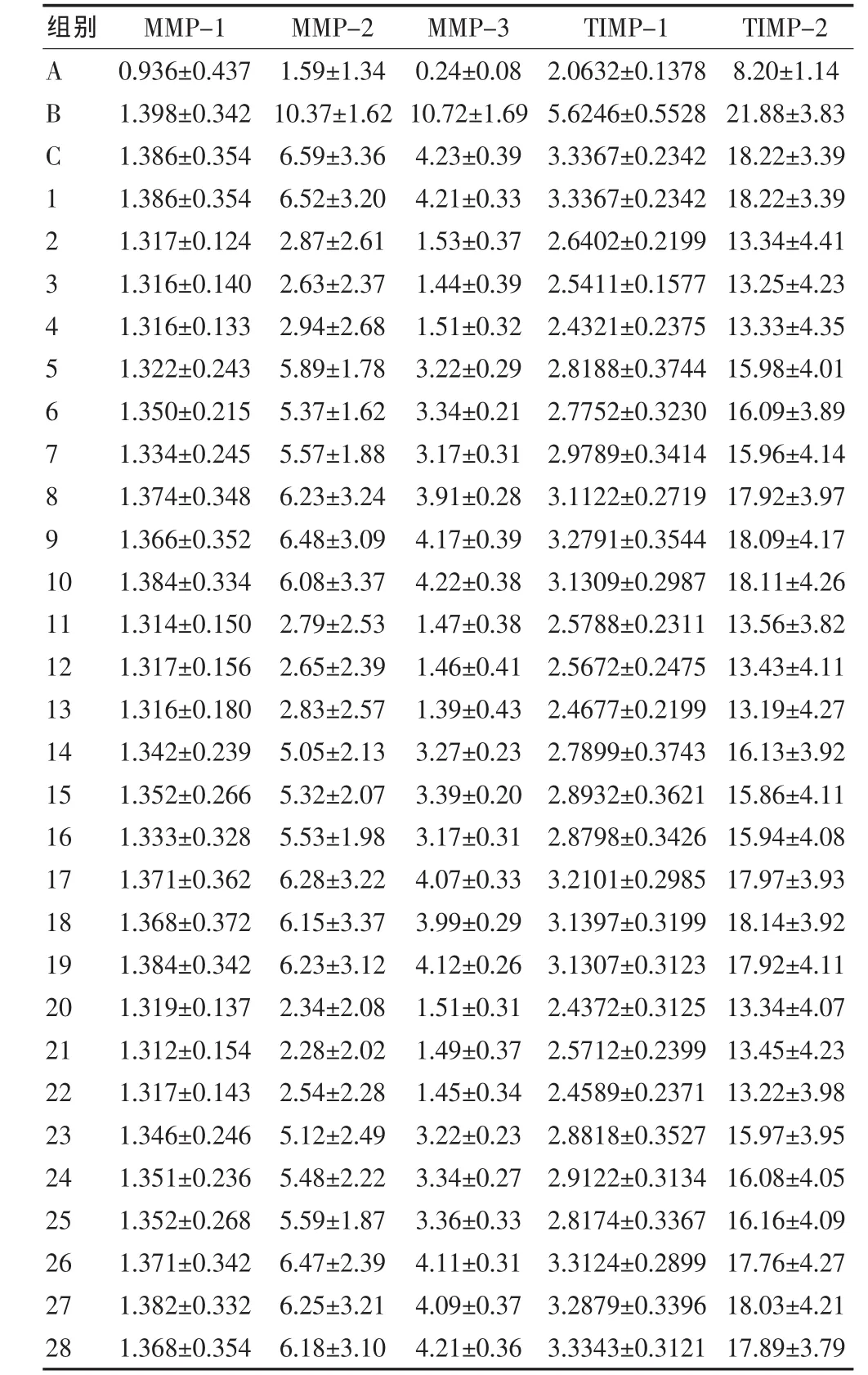
表4 各组大鼠肝组织中MMP-1、MMP-2、MMP-3及 TIMP-1、2 mRNA 表达水平（±s）

注：MMP-1：基质金属蛋白酶-1；MMP-2：基质金属蛋白酶-2；MMP-3：基质金属蛋白酶-3；TIMP-1：基质金属蛋白酶抑制物-1；TIMP-2：基质金属蛋白酶抑制物-2

ABC1234567891 0 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 0.936±0.437 1.398±0.342 1.386±0.354 1.386±0.354 1.317±0.124 1.316±0.140 1.316±0.133 1.322±0.243 1.350±0.215 1.334±0.245 1.374±0.348 1.366±0.352 1.384±0.334 1.314±0.150 1.317±0.156 1.316±0.180 1.342±0.239 1.352±0.266 1.333±0.328 1.371±0.362 1.368±0.372 1.384±0.342 1.319±0.137 1.312±0.154 1.317±0.143 1.346±0.246 1.351±0.236 1.352±0.268 1.371±0.342 1.382±0.332 1.368±0.354 1.59±1.34 10.37±1.62 6.59±3.36 6.52±3.20 2.87±2.61 2.63±2.37 2.94±2.68 5.89±1.78 5.37±1.62 5.57±1.88 6.23±3.24 6.48±3.09 6.08±3.37 2.79±2.53 2.65±2.39 2.83±2.57 5.05±2.13 5.32±2.07 5.53±1.98 6.28±3.22 6.15±3.37 6.23±3.12 2.34±2.08 2.28±2.02 2.54±2.28 5.12±2.49 5.48±2.22 5.59±1.87 6.47±2.39 6.25±3.21 6.18±3.10 0.24±0.08 10.72±1.69 4.23±0.39 4.21±0.33 1.53±0.37 1.44±0.39 1.51±0.32 3.22±0.29 3.34±0.21 3.17±0.31 3.91±0.28 4.17±0.39 4.22±0.38 1.47±0.38 1.46±0.41 1.39±0.43 3.27±0.23 3.39±0.20 3.17±0.31 4.07±0.33 3.99±0.29 4.12±0.26 1.51±0.31 1.49±0.37 1.45±0.34 3.22±0.23 3.34±0.27 3.36±0.33 4.11±0.31 4.09±0.37 4.21±0.36 2.0632±0.1378 5.6246±0.5528 3.3367±0.2342 3.3367±0.2342 2.6402±0.2199 2.5411±0.1577 2.4321±0.2375 2.8188±0.3744 2.7752±0.3230 2.9789±0.3414 3.1122±0.2719 3.2791±0.3544 3.1309±0.2987 2.5788±0.2311 2.5672±0.2475 2.4677±0.2199 2.7899±0.3743 2.8932±0.3621 2.8798±0.3426 3.2101±0.2985 3.1397±0.3199 3.1307±0.3123 2.4372±0.3125 2.5712±0.2399 2.4589±0.2371 2.8818±0.3527 2.9122±0.3134 2.8174±0.3367 3.3124±0.2899 3.2879±0.3396 3.3343±0.3121 8.20±1.14 21.88±3.83 18.22±3.39 18.22±3.39 13.34±4.41 13.25±4.23 13.33±4.35 15.98±4.01 16.09±3.89 15.96±4.14 17.92±3.97 18.09±4.17 18.11±4.26 13.56±3.82 13.43±4.11 13.19±4.27 16.13±3.92 15.86±4.11 15.94±4.08 17.97±3.93 18.14±3.92 17.92±4.11 13.34±4.07 13.45±4.23 13.22±3.98 15.97±3.95 16.08±4.05 16.16±4.09 17.76±4.27 18.03±4.21 17.89±3.79组别 MMP-1 MMP-2 MMP-3 TIMP-1 TIMP-2

根据规范化的区间数矩阵 B=（bij）31×13可得：

正理想点为 b+=（b1+，b12+， …b12+）， 其中，bj+=[bLAj，1]，j=1，2…，12；

负理想点为 b-=（b1-，b2-，…b12-），其中 bj-=[0，bBJR]，j=1，2…，12。

根据两区间数 a=[aL，aR]与 b=[bL，bR]的距离公式可知第i组的各指标值所组成的有序区间数组bi=（bi1，b12，…bi12)与正理想点b+=（b1+，b2+， … ，b12+)的距离为第i组的各指标值所组成的有序区间数组 bi=（bi1，bi2，…，bi12）与负理想点 b-=（b1-，b2-， …，b-12）的距离为

从而第i组的各指标值所组成的有序区间数组ba=（bi1，bi2，…bi12）的贴近度[10]为 di=di+/（di++di-），i=0，1，2，…，28。

由于方案 bi=（bi1，bi2，…bi12）与正理想点 b+=（1，1，…1）距离越小越优，而与负理想点 b-=（0，0，…，0）越大越优。 方案 bi=（bi1，bi2，…，bi12）的贴近度越小，则此方案越优。

3 讨论

经计算各组按贴近度由小到大排序得到各组优劣排序结果为：11组＞12组＞20组＞22组＞3组＞21组＞4组＞2组＞13组＞14组＞25组＞5组＞7组＞23组＞15组＞6组＞16组＞24组＞10组＞9组＞28组＞26组＞8组＞17组＞18组＞19组＞1组＞27组＞0组。 因此，第11组（柔肝化纤颗粒）最优，达到简化处方行为要素、增强药效、降低成本的目的，其作用机制可以体现以下四个方面：①保护肝细胞，防止肝细胞变性坏死；②促进肝内胶原蛋白降解，加速纤维组织重吸收；③脂质过氧化和抗脂质过氧化；④调节机体各种免疫应答。

[1]林寿宁，黄彬，朱永苹，等.壮肝逐瘀煎治疗慢性乙型肝炎40 例[J].陕西中医，2003，24（1）：25-26.

[2]王振常，毛德文，王丽，等.壮肝逐瘀煎对肝硬化门脉高压患者血流动力学影响临床观察[J].辽宁中医杂志，2008，35（7）：1045-1046.

[3]王振常，黄古叶.“壮肝逐瘀煎”治疗慢性乙型肝炎顽固性转氨酶升高 108 例临床观察[J].江苏中医，2008，40（1）：44-45.

[4]黄彬，林寿宁，黄贵华，等.中药对慢性乙型肝炎肝组织炎症坏死和纤维化的作用[J].辽宁中医杂志，2008，35（5）：713-714.

[5]刘力红.思考中医[M].桂林:广西师范大学出版社，2003：17.

[6]韩德五，马学惠，赵元昌.肝硬化动物模型的研究[J].山西医药杂志，1979，8（4）：1-3.

[7]李文才，张锦生，李华，等.肝组织羟脯氨酸含量测定方法的优化[J].上海医科大学学报，2000，27（4）：295.

[8]徐泽水.一种基于目标贴近度的多目标决策方法[J].系统工程理论与实践，2001，21（9）：101-103.

[9]和媛媛，周德群.区间数多属性决策问题的逼近理想点方法[J].统计与决策，2009，（24）：9-11.

[10]李健，王中兴.基于逼近理想点排序模糊数的方法[J].广西科学，2012，19（1）：21-24，27.