裂纹问题超奇异积分方程法的程序实现

杜云海，王 志，候建华

(郑州大学力学与工程科学学院，河南郑州450001)

0 引言

超奇异积分方程方法近些年来引起许多断裂力学工作者的关注并开展深入地研究［1-4］，在研究获得描述裂纹问题的超奇异积分方程组的基础上，建立计算应力强度因子的数值方法.由于利用了奇异积分的有限部积分，有效地解决了对奇异积分方程组求解的困难，使数值计算容易实现，计算的收敛速度也比较快捷，便于工程应用.由于目前尚无该方法在编程方面的相关报道，笔者根据近年来在相关研究［5-6］中对于数值方法的编程实现所积累的经验，就如何提高计算速度和输出满足精度要求的计算结果作以简要论述.

1 求解问题的线性方程组

作者的最新研究发现，双材料平面内一条任意曲线裂纹(长度为2a)问题均可以用一个以裂纹岸位移间断为基本未知量的超奇异积分方程组来描述，通过适当的变量与函数替换，对方程组进行归一化处理，并将未知的裂纹间断函数用第二类契比谢夫多项式表示，取该多项式在区间(-1，1)内的N个零点作为配置点，最终可把问题归结为对一个有2N个方程、2N个未知量的线性方程组的求解.这个线性方程组可用张量形式表示为

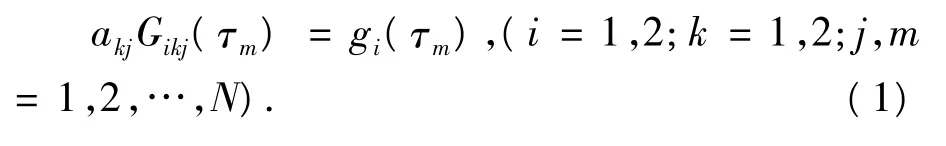
其基本未知量变成未知的第二类契比谢夫多项式系数akj.方程组(1)的系数Gikj(τm)与裂纹形状有关，以一条圆弧裂纹(图1)为例，方程组(1)的系数为

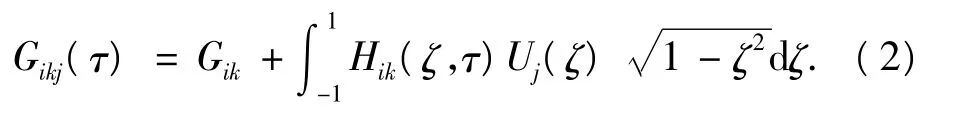
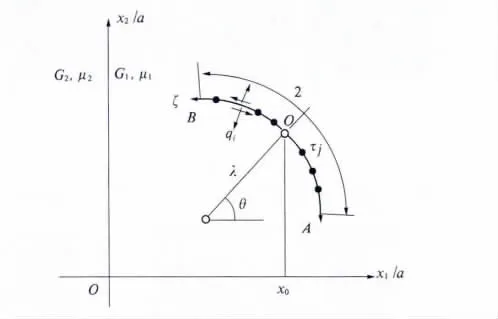
图1 双材料平面中的圆弧裂纹Fig.1 A arc crack in plane bimaterial

这里Hik(ξ，τ)为正常积分核函数，而Gik为奇异积分的有限部积分，具体形式与结果为

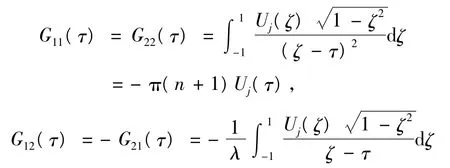
其中:Tj+1(τ)和Uj(τ)分别为第一类和第二类契比谢夫多项式，λ为圆弧半径比.方程组(1)中的gi(τm)决定于裂纹岸的分布载荷qi.ζ，τ表示裂纹弧长坐标.第二类契比谢夫多项式在区间(-1，1)上的N个零点为

2 应力强度因子计算公式

由断裂力学，裂纹尖端 A，B两点的应力强度因子可表达为

这里Fk(±1)由第二类契比谢夫多项式在区间端点的极限值来确定，可利用方程(1)的解进行计算，即

3 程序设计问题及其例程

在通过编程实现数值方法时，程序须按上述方法建立的关系来编写，这里不必赘述.但编程时须注意如何控制计算过程使之尽可能快速输出满足精度要求的应力强度因子.这样就必须把握好数值积分方法、方程组求解方法、以及适当配置方程个数以满足精度要求等几个环节.下面就这些关键问题逐一进行阐述.

3.1 关于数值积分的方法

数值积分是超奇异积分方程方法计算方程组系数的必需步骤，由于积分函数涉及契比谢夫多项式和复杂的积分核函数，实践表明，裂纹的位置越靠近双材料界面，采用一般数值积分法的收敛速度就越慢，如梯形积分法等会达到让人无法忍耐的缓慢程度.高斯积分法是精度相对较高而且较快的方法，但它只能配置固定的积分点，具有相同的计算时间.由于裂纹位置不同时，数值积分的收敛速度是不同的，这样就不利于控制在不同情况下获得统一的计算精度，或者不利于根据精度要求适当伸缩计算时间.相对而言，逐次分半加速法是一种比较适用的积分方法，既可以避免重复计算，又可根据设定的积分精度控制计算过程.假定设置精度为δ1(如取为1×10-4)，则当前、后两次计算结果相对误差小于δ1时便可返回计算结果，否则继续计算.

3.2 关于方程组求解的方法

对于线性方程组的求解，可以采用不同的方法，如主元素消去法、赛德尔迭代法等都可以快速求解.这里推荐比较简单的主元素消去法，它可以有效抑制系数矩阵变换过程所产生的计算误差.

3.3 关于应力强度因子精度的控制

在编写计算程序时，须注意计算结果应能输出满足精度要求的应力强度因子.这个问题可通过适当选择配置点数(N阶第二类契比谢夫多项式的N个零点)来解决.假如应力强度因子的计算精度要求为δ2=1×10-3，在裂纹位置远离双材料界面时，配置20几个点就足以满足精度要求;但在裂纹靠近界面时，就需要较多的配置点才能满足精度要求.为了得到刚好满足精度的计算结果，在编程时可以先设定一个配置点数的初值N0，通过计算求得应力强度因子后先用变量存储起来，然后再将配置点数增加一个增量ΔN，用点数N1=N0+ΔN重新计算，计算结果与上次结果比较，如满足精度要求则停止计算而输处结果，如不满足要求则再用点数N2=N1+ΔN进行计算，如结果与点数为N1的结果相比满足精度要求，则输出结果，否则再增加点数ΔN进行计算，如此类推，直至当下点数的计算结果与上次结果相比满足精度要求为止，这样最终就得到稳定的应力强度因子值.

采用上述方法，建立和求解方程组的次数至少需要两次，一般3到4次计算就可获得理想的计算结果.当然，循环次数肯定与最初设置的配置点数N0有关.若初始点数小，数值积分速度快，但在控制应力强度因子精度的情况下可能会造成更多的循环计算次数;若初始点数大，数值积分速度慢，但在控制精度情况下的循环计算次数反而会少.故选择适当的初始点数可有效减少计算所需的总机时.以下是圆弧裂纹问题采用这种算法的Fortran9.0主程序，其中配置点数的初始值选为N0=n1=38.每次循环计算增加点数选为ΔN=4，应力强度因子控制精度为1×10-3.

program sclyhlw

double precision ka(2)，kb(2)，k1a(2)，

*k1b(2)，tb，rb，xob，xta0，xta1，gs1(2，0:100)，

*gs(2，2，0:100，0:100)，fy(2) ，a(2，0:100)，

*g(2，0:100，0:202)，s(0:100)，g1(0:201，0:202)，

*x(202)，rs(0:100，0:100)，fa(2)，fb(2)，

*g11(202，203)，ss1，dta，dtb

character*20 jsjg

write(* ，*)＇输入结果文件名:'

read(*，*)jsjg

open(6，file=jsjg，status='new')

write(* ，*)'输入参数:tb，rb，xob，xta0，fy(1)

*，fy(2)'

read(* ，*)tb，rb，xob，xta0，fy(1)，fy(2)

write(6，*)tb，rb，xob，xta0，fy(1)，fy(2)计算方程组系数

n1=38

xta1=xta0*3.1415927D-00/180.00

do 10 k=1，2

ka(k)=0.0

kb(k)=0.0

10 continue

20 do 100 i=1，2

do 90 k=1，2

do 80 j=0，n1

s(j)=dcos((j+1)*3.1415927d-00/

* (n1+2.0))

gs1(i，j)=-fy(i)*3.1415927

do 70 n=0，n1

if(i.eq.1.and.k.eq.1)then

if(s(j).gt.1.0-5.0d-05)then

rs(j，n)=-3.1415927*(n+1)＊＊2

else if(s(j).lt.-1.0+5.0d-05)then

rs(j，n)=-3.1415927*(n+1)＊＊2*(-1)＊＊n

else

rs(j，n)=-3.1415927*(n+1)* dsin((n+1)*

＊dacos(s(j)))/dsin(dacos(s(j)))

end if

else if(i.eq.1.and.k.eq.2)then

if(s(j).gt.1.0-5.0d-05)then

rs(j，n)=3.1415927/rb

else if(s(j).lt.-1.0+5.0d-05)then

rs(j，n)=3.1415927*(-1)＊＊(n+1)/rb

else

rs(j，n)=3.1415927*dcos((n+1)*

＊dacos(s(j)))/rb

end if

else if(i.eq.2.and.k.eq.1)then

if(s(j).gt.1.0-5.0d-05)then

rs(j，n)=-3.1415927/rb

else if(s(j).lt.-1.0+5.0d-05)then

rs(j，n)=-3.1415927*(-1)＊＊(n+1)/rb

else

rs(j，n)=-3.1415927*dcos((n+1)*

＊dacos(s(j)))/rb

end if

else

if(s(j).gt.1.0-5.0d-05)then

rs(j，n)=-3.1415927*(n+1)＊＊2

else if(s(j).lt.-1.0+5.0d-05)then

rs(j，n)=-3.1415927*(n+1)＊＊2*(-1)＊＊n

else

rs(j，n)=-3.1415927*(n+1)* dsin((n+1)*

＊dacos(s(j)))/dsin(dacos(s(j)))

end if

end if

调用数值积分子程序szjf，并将结果存于四维临时数组gs

call szjf(i，k，n，s(j)，tb，ss1，rb，xob，xta1)

gs(i，k，j，n)=rs(j，n)+ss1

write(* ，'(5x，3hg( ，i1，1h，，i1，1h，，i2，1h，，i2，

*4h)= ，f18.8)')i，k，j，n，gs(i，k，j，n)

70 continue

80 continue

90 continue

100 continue

整理方程组，将系数赋给一个二维数组g11

write(*，*)'solve equtions:'

do 200 i=1，2

do 190 j=0，n1

do 180 n=0，n1

g(i，j，n)=gs(i，1，j，n)

g(i，j，n1+1+n)=gs(i，2，j，n)

180 continue

g(i，j，2*n1+2)=gs1(i，j)

190 continue

200 continue

do 270 j=0，n1

do 260 n=0，2*n1+2

g1(j，n)=g(1，j，n)

g1(j+n1+1，n)=g(2，j，n)

260 continue

270 continue

do 280 i=1，2*n1+2

do 275 j=1，2*n1+3

g11(i，j)=g1(i-1，j-1)

275 continue

280 continue

write(* ，285)((g11(i，j)，j=1，2*n1+3)，i=1，2*n1+2)

285 format(1x，11f7.4)

调用主元素法子程序zyss求解方程组g11，并将结果赋给二维数组a

call zyss(g11，x，2*n1+2，2*n1+3)

write(*，*)'outo zyss'

do 290 n=0，n1

a(1，n)=x(n+1)

a(2，n)=x(n+n1+2)

write(* ，'(5x，4ha(1，，i2，2h)= ，f12.6，10x，

*4ha(2，，i2，2h)= ，F12.6)')n，a(1，n)，n，a(2，n)

290 continue

利用数组a计算应力强度因子，并与上次结果比较，在误差dta、dtb不满足精度要求的条件下，增加配置点数，暂存当前结果，并返回到2 0号语句重新计算

do 600 k=1，2 fa(k)=0.0 fb(k)=0.0

do 500 n=0，n1

fa(k)=fa(k)+a(k，n)*(n+1)*(-1)＊＊n

fb(k)=fb(k)+a(k，n)*(n+1)500 continue

k1a(k)=fa(k)

k1b(k)=fb(k)

dta=dabs(k1a(k)-ka(k))

dtb=dabs(k1b(k)-kb(k))

if(dta.gt.1.0d-03.or.dtb.gt.1.0d-03)then

n1=n1+4

if(n1.gt.100)then

write(* ，*)'n1＞100，stop!'

stop

end if

ka(k)=k1a(k)

kb(k)=k1b(k)

goto 20

end if

输出满足精度的强度因子当前值k1a、k1b

write(6，'(1x，1x，3htb= ，f5.2，1x，3hrb= ，f8.2，1x，4h

*xob=，f8.2 ，1x，5hxta0=，f5.2，1x，6hfy(1)=，f5.2，

*1x，6hfy(2)= ，f5.2，1x，2hk= ，i1，1x，3hka= ，f7.3，1x，

*3hkb=，f7.3)')tb，rb，xob，xta0，fy(1)，fy(2)，k，

*k1a(k)，k1b(k)600 continue

end

该程序将计算结果写入开始运行时文本变量“jsjg”要求赋值的数据文件.

3.4 其他问题

在程序中还需要正常积分核函数，这需要根据正常积分核函数的具体形式编制函数子程序，如上述例程中的“sjf”，由于积分核函数的关系复杂，这里不再给出相应的例程，具体函数的形式可关注作者近期的相关文献.

3.5 算例

启动程序后，按要求须首先输入计算结果的存储文件名(如“JG”)，然后再输入弹性模量比、圆弧半径比、圆弧中点坐标比、圆弧中点半径与x轴的夹角、以及裂纹岸载荷等所需参数，输入后即可自动实施计算，并将输入数据与运行结果写入开始定义的存储文件“JG”.用Windows系统附件的记事本或写字板工具可打开浏览结果文件“JG”，显示内容如下所示:

输入参数:tb，rb，xob，xta0，fy(1)，fy(2)

1.000000000000000 5.000000000000000

3.000000000000000 0.000000000000000

1.000000000000000 0.000000000000000

tb=1.00 rb=5.00 xob=3.00 xta0=.00 fy(1)=1.00 fy(2)=.00 k=1 ka=.980 kb=.980 tb=1.00 rb=5.00 xob=3.00 xta0=.00 fy(1)=1.00 fy(2)=.00 k=2 ka=.098 kb=-.099

这一计算过程所用时间一般不超过5 min.

4 结论

基于双材料平面中裂纹岸受分布载荷作用的圆弧裂纹问题的归一化超奇异积分方程组及其数值方法，重点讨论了用Fortran9.0编程工具进行程序设计中需要考虑的数值积分方法、方程组求解方法、以及控制应力强度因子精度的循环算法等相关问题，并给出部分例程编码.实际例程的运行结果表明，所采用的算法可以获得较高运算速度和满足精度要求的应力强度因子.

［1］ISIDA M，NOGUCHI H.An arbitrary array of cracks in bonded semi-infinite bodies under in-plane loads［J］.Trans.JSME，1983，49:36-45.

［2］DONG C Y，LEE K Y.A new integral equation formulation of two-dimensional inclusion-crack problems［J］.International Journal of Solid and Structure，2005，42:5010-5020.

［3］KAYA A C，ERDOYAN F.On the solution of integral equations with strongly singular kenels［J］.Quarterly of Applied Mathematics，1987(A5):105-122

［4］MARTIN P A，IZZO F J R.On boundary integral equations for crack problems［J］.Proc.R.Soc.Lond，1988，421:341-355.

［5］杜云海，乐金朝.双材料平面斜裂纹问题超奇异积分方程方法［J］.机械强度，2004，26(3):326-331.

［6］杜云海，吕存景，董栋，等.双材平面中环形界面环向裂纹问题的超奇异积分方程方法［J］.机械强度，2006，28(5):733-738.