基于扰动观测器的机器人位置控制器设计*
2013-09-12游有鹏
张 宇,游有鹏
(南京航空航天大学机电学院,南京 210016)
0 引言
扰动观测器DOB(Disturbance Observer),顾名思义是通过将外部扰动及模型参数变化造成的实际对象和名义模型输出的差异等效到控制输入端,即观测出等效干扰,然后在控制中引入等效补偿,实现对干扰的完全抑制[1]。由于在伺服系统中采用扰动观测器无需安装任何额外传感器,且计算量小,具有较好的扰动抑制能力,因而扰动观测器广泛应用于伺服系统的驱动中。国内外学者开展了很多对于扰动观测器的研究,Takaji Umeno等[2]人给出了扰动观测器Q滤波器的一般形式。S.Endo等[3]人将扰动观测器与零相位误差跟踪控制器(ZPETC)相结合应用于高速位置控制系统中取得较好的控制效果。K.Yamada等[4]分析了扰动观测器的扰动抑制能力与Q滤波器的阶数之间的关系,指出Q滤波器的阶数越高,扰动抑制能力越强。I.Godler等[5]人分析了扰动观测器系统的振动与控制器采样周期、Q滤波器截止频率等因素之间的关系,给出了Q滤波器截止频率的设计准则。清华大学黎坚等[6]人分析了数字控制时延对扰动观测器性能的影响。哈尔滨工业大学孙立宁等[7]人通过对比考虑和忽略时间延时环节两种情况下扰动观测器的品质,得出引入带有时间延时的扰动观测器将获得更好的扰动抑制效果。清华大学杨开明等[8]人将扰动观测器应用于直线电机精密工作台的位置控制中,取得较好的控制效果,较之仅采用PD的位置控制器,工作台的静态定位精度提高了0.3μm,120mm/s匀速运动时的轨迹跟踪误差提高了2μm。
机器人的动力学方程是一组非线性、强耦合、多变量的二阶微分方程组,这使得动力学方程的求解运算量巨大,因而不适用于实时计算。现有工业机器人的位置控制通常采用基于PID+前馈的位置控制算法,而未将机器人的动力学应用于位置控制,这大大限制了位置控制的跟踪精度。本文将扰动观测器应用于机器人的控制,通过扰动观测器直接观测并补偿关节重力、摩擦力、科氏力、离心力的变化以及关节惯量的变化等因素所引入的扰动力矩,使得对于位置控制器和速度控制器而言,关节电机可近似视为一个具有恒定惯量且无负载的控制对象,有效的实现了机器人动力学的解耦[9]。最后分析了扰动观测器系统的稳定性,并通过实验验证了扰动观测器应用于机器人控制的有效性。
1 扰动观测器的基本原理
扰动观测器的框图[10]如图1所示,u为输入信号、d为干扰信号、y为输出信号、ξ为测量噪声、P(s)为实际模型、P-1(s)为实际模型的逆,由于无法获取准确的实际模型,因而引入实际模型的名义模型即Pn(s),名义模型是实际模型的近似,P-1n(s)为名义模型的逆,Q(s)为低通滤波器,称为Q滤波器。

图1 扰动观测器框图
由图1可得引入扰动观测器后系统的输出:

对于运动控制系统而言,外部扰动信号d通常分布在低频段,而测量噪声ξ通常分布在高频段[11]。设计Q(s)为低通滤波器,则在低频段Q(s)≈1,则Guy(s)≈Pn(s)、Gdy(s)≈0、Gξy(s)≈ -1;而在高频段,Q(s)≈0,则Guy(s)≈P(s)、Gdy(s)≈P(s)、Gξy(s)≈0。可见低频段输出信号y与扰动信号d无关,且与输入信号u呈现出名义模型的传递函数关系,可见扰动观测器对扰动的抑制作用。
2 含有扰动观测器的机器人位置控制器设计
应用于工业机器人的的位置控制系统通常采用图2所示的基于PID+前馈的位置控制系统。由于电流环的控制周期远小于位置环和速度环的控制周期,因而在分析位置控制器和速度控制器时可将电流环等效为常数1。图中,Gp(s)、Gv(s)分别为位置环控制器(PID)和速度环控制器(PI),F1(s)和F2(s)分别为速度前馈环节和加速度前馈环节,Kt为电机电枢常数,J为关节转动惯量,Td为负载力矩扰动,包括各关节重力、摩擦力、科氏力、向心力等因素变化所造成扰动力矩。
从图2中虚线所示部分可以看出,关节转速输出信号与电流指令信号关系如式(5)所示。


图2 常规机器人位置控制系统
即转速输出信号与负载的力矩扰动Td、关节的转动惯量J均相关。机器人实际运动过程中,不仅重力、摩擦力、科氏力、向心力等因素产生的扰动力矩Td不断变化,而且当机器人处于不同位姿时,各关节的等效惯量J也是不同的,且Td、J的变化呈现多变量、强耦合的关系,这大大限制了机器人位置控制的精度。
将扰动观测器应用于机器人位置控制器,所设计机器人位置控制系统框图如图3所示。其中,Ktn为电机名义电枢常数,Jn为关节名义转动惯量。
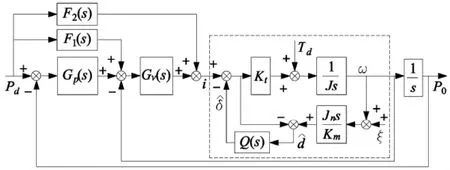
图3 基于扰动观测器的机器人位置控制系统
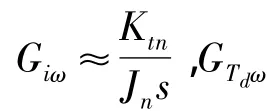

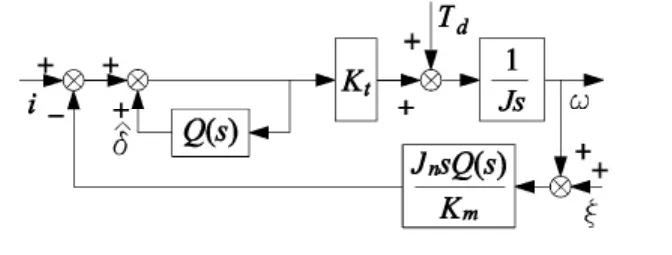
图4 振动观测器等效框图
对比式(5)、式(6)可知,引入扰动观测器之后,电机的转速输出仅与电流指令信号、名义电枢常数、名义惯量以及测量噪声有关,而与负载扰动力矩、关节实际惯量无关,这使得对于位置控制器和速度控制器而言,关节电机可近似视为一个具有恒定惯量且无负载的控制对象,即实现了机器人动力学的解耦。
3 扰动观测器的稳定性分析


图5 扰动观测器加速度环等效图
由图5可推导出等效加速度闭环的传递函数如式(7)所示。

可见当选用一阶巴特沃斯滤波器作为Q滤波器时,加速度环的闭环特征根为-mg,加速度闭环为稳定的系统。
4 实验验证
如图6所示,图6a所示为自行设计的以MAXON RE25直流伺服电机作为驱动电机的机器人运动平台,图5b所示为以TMS320F2812 DSP和EP1C6Q240C8N FPGA为硬件平台设计的集驱动和控制为一体的四轴机器人全数字控制器。
设计如图6c所示测试实验,独立控制关节J1和J2分别以梯形升降速方式同时从位置1运行至位置2,在此过程中,由机器人动力学方程可知关节J1的力矩存在明显的变化,且关节J1的等效惯量也发生了明显的变化。图7a为仅采用PID+前馈的位置控制效果,在图示A点,电机克服了传动系统的间隙后,负载力矩迅速增大,轨迹控制存在明显的跟踪误差,在B、C等处由于重力、摩擦力、科氏力、离心力以及惯性力等因素变化造成扰动力矩的变化均引起了较大的位置跟踪误差。当引入扰动观测器以后,控制效果如图7b所示,控制器可有效抑制负载扰动的变化所造成的跟踪误差。采用扰动观测器之后,由于测量噪声ξ的作用,关节速度存在一定的抖动,但较之未采用扰动观测的控制器,控制效果明显提高。
5 结束语
(1)本文在常规PID+前馈的机器人位置控制策略基础上,进一步引入负载扰动的实时观测和补偿技术,有效的实现了机器人动力学的解耦;
(2)分析了采用一阶巴特沃斯滤波器作为Q滤波器时系统的稳定性;
(3)在自行设计的集控制和驱动为一体的机器人全数字控制器平台上开展了验证实验,结果表明将扰动观测器应用于机器人控制可明显减小机器人位置控制的跟踪精度,且运算量小。

图6 机器人实验平台

图7 关节J1速度及跟踪误差
[1]贾松涛,朱煜,杨开明,等.精密工作台扰动观测器的设计[J].微细加工技术,2007(4):39-42.
[2]T.Umeno,Y.Hori.Robust speed control of DC servomotors using modern two degrees-of-freedom design[J].IEEE Transaction on Industrial Electronics.1991,38(5):363-368.
[3]S.Endo,M.Tomizuka,Y.Hori.Robust digital tracking controller design for high-speed positioning systems[J].Control Engineering Practice.1996,4(4):527 -536.
[4]K.Yamada,S.Komada,M.Ishida,et al.Analysis and classical control design of servo system using high order disturbance observer[C]//23rdInternational Conference on Industrial Electronics and Instrumentation.New Orleans:IECON,1997:9-14.
[5]I.Godler,H.Honda,K.Ohnishi.Design guidelines for disturbance observer’s filter in discrete time[C]//7thInternational Workshop on Advanced Motion Control.Piscataway:IEEE Press,2002:390 -395.
[6]黎坚,杨耕,窦曰轩.数字控制时延对扰动观测器性能的影响[J].电气传动,2003(2):18-20.
[7]孙立宁,崔晶,曲东升,等.基于离散型扰动观测器的直线电机控制研究[J].机械工程学报,2004,40(12):164-167.
[8]杨开明,叶佩清,游华云,等.直线电机精密工作台扰动观测器设计[J].机械科学与技术,2005,24(12):1430-1432.
[9]M.Nakao,K.Ohnishi,K.Miyachi.A Robust decentralized joint control based on interference estimation[C]//International Conference on Robotics and Automation.Raleigh:IEEE Press,1987:326 -331.
[10]蓝晨阳.基于扰动观测器的超精密宏微驱动定位技术研究[D].哈尔滨:哈尔滨工业大学,2010.
[11]何忠亮.基于新扰动观测器的鲁棒控制系统设计[D].广州:华南理工大学,2010.
[12]于艾,杨耕,徐立文.具有扰动观测器调速系统的稳定性分析及转速环设计[J].清华大学学报(自然科学版),2005:45(4):521-524.
