GF（q）上pn－周期序列的k错线性复杂度＊

周建钦，欧阳孔礼

（1.安徽工业大学计算机学院，安徽马鞍山 243002；2.杭州电子科技大学通信工程学院，浙江杭州 310018）

GF（q）上pn－周期序列的k错线性复杂度＊

周建钦1，2，欧阳孔礼1

（1.安徽工业大学计算机学院，安徽马鞍山 243002；2.杭州电子科技大学通信工程学院，浙江杭州 310018）

周期序列的错误线性复杂度是度量密钥流稳定性的一个重要指标.首先改写GF（q）上pn周期序列的k错线性复杂度快速算法，给出其m紧错线性复杂度的快速算法；然后研究相应k错线性复杂度的误差向量，得到计算误差向量的算法，即在此误差向量下，可以实现原始序列的k错线性复杂度.其中p为奇素数，q是模p2的一个本原根.

k错线性复杂度；m紧错线性复杂度；误差向量

1 相关定义

在流密码理论研究中，密钥流序列的线性复杂度是度量其强度的一个重要指标［1－2］.为了抵御Berlekamp-Massey［1－2］算法的攻击，序列的线性复杂度要尽可能地高.然而在保证序列线性复杂度足够高的同时，还要要求在改变少量比特的情况下，序列的线性复杂度下降得较小.为此，丁存生等［3］率先给出一些度量序列稳定性的指标，随后国外学者Stamp M等［4］独立提出了k错线性复杂度的概念来研究序列的稳定性.

定义1［1］周期序列的线性复杂度定义为能够产生周期序列s的最小线性移位寄存器（LFSR）的阶数，记为c（s）.

定义3［5］序列s的最小错误minerror（s）定义为满足不等式ck（s）＜c（s）的最小正整数.即为使其线性复杂度下降，至少要改变序列s的元素数目.

综合上述概念，文献［6－7］提出了m紧错线性复杂度的概念来研究周期序列的稳定性，并给出了2n周期和pn周期二元序列的m紧错线性复杂度快速算法.

定义4［6－7］序列s的m紧错线性复杂度记为（km，cm），其中km表示序列k错线性复杂度的第m个下降点，cm表示km错线性复杂度.

若有周期序列s，显然，当m＝0时，c0即为原序列s的线性复杂度；当m＝1时，k1即为minerror（s），c1为序列s的k1错线性复杂度.

例如，设序列s是一个周期为81的5元序列，其第一周期s81＝141022134 423301104 001134332 143022134 423301104 001134332 143022134 423301104 001134302，则可以得到序列s的k错线性复杂度曲线和m紧错线性复杂度曲线分别如图1，2所示.

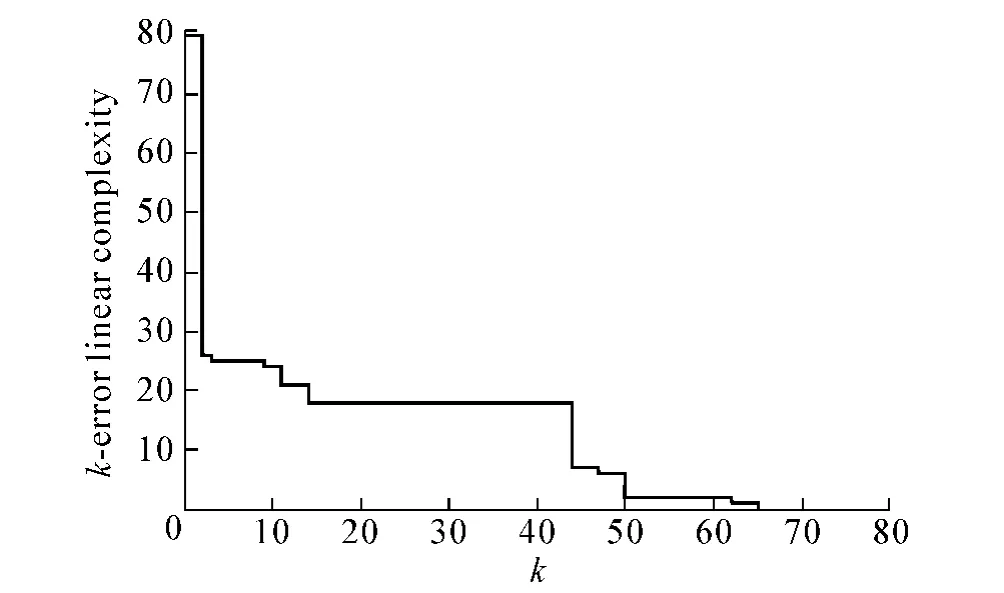
图1 k错线性复杂度曲线

图2 m紧错线性复杂度曲线

关于求2n周期二元序列k错线性复杂度的Stamp-Martin算法［4］有一个重要的思想［7］：如果算法中第j次循环可使线性复杂度降低的值记为dj，那么以后所有循环可能降低线性复杂度的总和不会大于dj.若一个周期序列k错线性复杂度的算法与Stamp-Martin算法类似，则称该算法满足Stamp-Martin模式.易证明，满足Stamp-Martin模式的算法也可以类似地拓展为m紧错线性复杂度算法.对于一些现有的求线性复杂度的快速算法，如GF（2）上2npm周期序列线性复杂度的快速算法［8］，这样的算法不容易推广成为求k错线性复杂度的快速算法.而对于给定的值m，现有的线性复杂度的快速算法一般均可以推广为求m紧错线性复杂度的快速算法.m紧错线性复杂度同时包括多个研究序列强度及稳定性的概念（线性复杂度、k错线性复杂度以及序列最小错误minerror（s）等），因此具有重要的研究意义与价值.

文献［6－7］给出了2n周期和pn周期二元序列的m紧错线性复杂度快速算法，文献［9］给出了改写的Stamp-Martin算法与计算误差向量的快速算法.笔者通过改写文献［10］中GF（q）上pn周期序列的k错线性复杂度的快速算法，给出了其m紧错线性复杂度和相应误差向量的快速算法，并通过实例进行说明其有效性.这里p是奇素数，q是模p2的一个本原根.

2 改写的k错线性复杂度快速算法

文献［10］给出了确定q元pn周期序列k错线性复杂度的快速算法，以下称为魏－董－肖算法.在魏－董－肖算法中，cost只计算了为改变当前序列中的ai而多付出的代价.事实上，可以改变cost的定义为：为改变当前序列中的ai而必须改变原始序列的比特数.这样即使保持当前元素位置不变时也可能需要付出代价，即此时cost也可能不为0.现首先对魏－董－肖算法进行改写，改写后的算法与魏－董－肖算法的时间复杂度相同，但易于理解和推广.

下面给出改写的q元pn－周期序列k错线性复杂度的快速算法.

设s＝（s0，s1，...）为GF（q）上周期N＝pn的序列，其中p是奇素数，q是模p2的一个本原根，sN＝（s0，s1，...，sN－1）是s的第1个周期，记a＝（a0，a1，...，al－1）.计算s的k错线性复杂度的算法如下所示.

算法1 初始值a←sN，l←pn，c←0，cost［i，ai］←0，当0≤h≤q－1且h≠ai时，cost［i，h］←1（i＝0，1，...，l－1）.

最终可得周期序列s的k错线性复杂度ck（s）＝c.

在算法1中，k是一个固定的值，cost［i，h］的定义更合理，使得计算T和新的cost［i，h］变得容易理解.由如下定理1，2和文献［10］中的相关证明，易知算法1的正确性.

定理1 cost［i，ai］≤cost［i，h］（h＝0，1，...，q－1；i＝0，1，...，l－1；l＝pn，pn－1，...，p，1）.

证明 当l＝pn时，若h＝ai，则cost［i，h］＝0，若h≠ai，则cost［i，h］＝1，成立.若第j步T≤k，则cost［i，ai］＝Ti≤Tih＝cost［i，h］；若第j步T＞k，由cost［i＋jl，ai＋jl］≤cost［i＋jl，ai＋jl＋dj］，则

3 m紧错线性复杂度的快速算法

对魏－董－肖算法的改写，没有影响算法的结构，而修改后的算法更方便推广为计算m紧错线性复杂度的快速算法.

在上述算法1的基础上，通过适当修改，易求GF（q）上pn周期序列的m紧错线性复杂度.具体修改如下：

（a）在初始值中添加Tmin←pn；

（b）在（ⅳ）最前部添加语句“若T＜Tmin，则Tmin←T”.

（c）在（ⅱ）中c←c＋1之后添加语句“若cost［0，0］＜Tmin，则Tmin←cost［0，0］”.

注 Tmin表示的是使线性复杂度再次下降需要改变原始序列的最小比特数.

作上述修改后得到的算法记为算法2.

在首次调用算法2时，此时k＝0，本次调用结束后即可以得到的序列s的线性复杂度c0（此时k＝0，0错线性复杂度即为原始序列的线性复杂度），除此之外还可以得到使得线性复杂度第1次下降需要改变的比特数目Tmin；此时令k＝Tmin，再次调用算法2，记当前k为k1，可以得到序列的k1错线性复杂度c1和使得线性复杂度再次下降需要改变的比特数目Tmin；通过反复调用算法2，即可得到序列s的m紧错线性复杂度.

例1 设s是GF（5）上的周期为81的序列，其第1个周期s81＝141022134 423301104 001134332 143022134 423301104 001134332 143022134 423301104 001134302，其m紧错线性复杂度求解过程如下：此时l＝81，11次调用算法2，依次得到（0，80），（2，26），（3，25），（9，24），（11，21），（14，18），（44，7），（47，6），（50，2），（62，1），（65，0）.由此易得图2所示序列s的m紧错线性复杂度曲线.

若按照魏－董－肖算法来计算序列的k错线性复杂度曲线，先后共需要调用算法82次，得到图1所示序列s的k错线性复杂度曲线，而利用算法2只需要11次.文献［11］也给出了确定pn－周期的q元序列k错线性复杂度曲线的算法，但是利用文中的算法更易于理解.另外文献［11］中部分计算结果是错误的：文中c1（s）＝79，c3（s）＝c4（s）＝26，c9（s）＝c10（s）＝c11（s）＝c12（s）＝c13（s）＝25，c14（s）＝c15（s）＝c16（s）＝21.事实上，正确结果为c1（s）＝80，c3（s）＝c4（s）＝25，c9（s）＝c10（s）＝c11（s）＝c12（s）＝c13（s）＝24， c14（s）＝c15（s）＝c16（s）＝18.

由例1可知，周期序列s的线性复杂度、线性复杂度每次下降所需要改变的比特数以及下降后的值，都可由求解m紧错线性复杂度的过程计算出来.因此，对于m紧错线性复杂度的研究具有重要的意义与价值.

4 误差向量的计算

在k错线性复杂度的实际应用中，误差向量的计算是非常重要的.在算法1的基础上，给出k错线性复杂度对应的误差向量.即在此误差向量下，原始序列可以实现k错线性复杂度ck（s）.

以下给出计算GF（q）上pn周期序列计算对应误差向量的有效算法，其中p和q都是奇素数，并且q是模p2的一个本原根.

（ⅴ）start←start－1，l←1，转向（ⅵ）.

（ⅵ）若l＜pn－1，则转向（ⅶ）；否则error＝begin－s（mod q），停止.

最后可同时得到序列s的k错线性复杂度ck（s）＝c与使得ck（s）＝c（s＋e）成立的误差向量e＝error.

算法3中，changeto［i，h］存放的是：为得到当前序列中的cost［i，h］，上一步序列中ai，ai＋l，...，ai＋（p－1）l需要改变成的值.算法3最初得到的begin记录上一步，a，...，a应该变成的值h0，h1，...，hp－1，再根据changeto［start＋i，hi］得到上一步序列应该变成的值，i＝0，1，...，p－1；以此类推，最后得到原始序列应该变成的新序列，从而推导出误差向量error.

例2 五元序列的一个周期s81＝141022134 423301104 001134332 143022134 423301104 001134332 143022134 423301104 001134302，求4错线性复杂度c4（s）及对应的误差向量.

最后，序列s的4错线性复杂度c4（s）＝25，对应的误差向量为error，利用Berlekamp-Massey算法容易验证s＋error的线性复杂度确实为25.

5 结语

在魏－董－肖算法的基础上，首先改写GF（q）上pn周期序列的k错线性复杂度快速算法，给出了其m紧错线性复杂度算法；然后给出计算其误差向量的有效算法，即在此误差向量下，能够实现原序列的k错线性复杂度ck（s）.其中p和q都是奇素数，并且q是模p2的一个本原根.

［1］ MASSEY J L.Shift Register Synthesis and BCH Decoding［J］.IEEE Transactions on Information Theory，1969，1 5（1）：122－127.

［2］ BLACKBURN S R.Fast Rational Interpolation，Reed-Solomon Decoding and the Linear Complexity Profiles of Sequences［J］.IEEE Transactions on Information Theory，1997，43（2）：537－548.

［3］ DING Cun-sheng，XIAO Guo-zhen，SHAN Wei-juan.The Stability Theory of Stream Ciphers［M］.LNCS 561.Berlin：Springer-Verlag，1991：85－88.

［4］ STAMP M，MARTIN C F.An Algorithm for the k-Error Linear Complexity of Binary Sequences with Period 2n［J］.IEEE Transactions on Information Theory，1993，39（4）：1 398－1 401.

［5］ KUROSAWA K，SATO F，SAKATA T，et al.A Relationship Between Linear Complexity and k-Error Linear Complexity［J］.IEEE Transactions on Information Theory，2000，46（2）：694－698.

［6］ ZHOU Jian-qin，CHENG Shang－guan，ZHAO Ze-mao.Computing the m-Tight Error Linear Complexity of Periodic Binary Sequences［J］.IEEE Computer Society，CIS 2009，2009：386－390.

［7］ 周建钦，上官成，赵泽茂.若干二元周期序列的紧错线性复杂度［J］.计算机工程与应用，2011，47（10）：49－53.

［8］ 魏仕民，肖国镇，陈 钟.确定周期为2npm二元序列线性复杂度的快速算法［J］.中国科学：E辑，2002，32（3）：401－408.

［9］ 徐喜荣，周建钦.关于求周期序列k错线性复杂度的Stamp-Martin算法［J］.微电子学与计算机，2007，24（4）：28－31.

［10］ 魏仕民，董庆宽，肖国镇.确定周期序列k－错线性复杂度的一个快速算法［J］.西安电子科技大学学报，2001，2 8（4）：421－424.

［11］ 白恩键，谭示崇，肖国镇.确定周期为pn的q元序列k－错线性复杂度曲线的一个快速算法［J］.西安电子科技大学学报，2004，31（3）：388－393.

（责任编辑 向阳洁）

On k-Error Linear Complexity of pn-Periodic Sequences over GF（q）

ZHOU Jian-qin1，2，OUYANG Kong-li1
（1.Computer Science School，Anhui University of Technology，Ma’anshan 243002，Anhui China；2.College of Telecommunication，Hangzhou Dianzi University，Hangzhou 310018，China）

Error linear complexity of periodic sequences is an important indicator of the stability of the key stream.First，the algorithm for computing the k-error linear complexity of a sequence with a period pnover GF（q）is rewritten，and an efficient algorithm for m-tight error linear complexity of this sequence is given.Secondly，a method is given for computing an error vector which gives the k-error linear complexity.Here pis an odd prime and qis a primitive root modulus p2.

k-error linear complexity；m-tight linear complexity；error vector

TN911.1；TN918.1

A

10.3969／j.issn.1007－2985.2013.06.012

1007－2985（2013）06－0041－06

2013－04－13

安徽省自然科学基金资助项目（1208085MF106）

周建钦（1963－），男，山东巨野人，安徽工业大学计算机学院教授，主要从事理论计算机科学、密码学研究.