应用凸函数证明不等式的2点注记＊

雍龙泉

（陕西理工学院数学与计算机科学学院，陕西汉中 723001）

应用凸函数证明不等式的2点注记＊

雍龙泉

（陕西理工学院数学与计算机科学学院，陕西汉中 723001）

基于凸函数的判别定理，指出了在应用凸函数证明不等式时应注意的问题，即二阶导数是否存在决定了利用凸函数证明不等式的出发点.之后，应用凸函数的性质证明了康托洛维奇不等式的矩阵形式.

凸函数；不等式；康托洛维奇不等式

定义1［1］设f（x）定义在［a，b］上，若对∀x，y∈［a，b］及∀α∈［0，1］，有f［αx＋（1－α）y］≤αf（x）＋（1－α）f（y），则称f（x）为［a，b］上的凸函数.

定理1，2为凸函数的判别［1－2］.

定理2 设f（x）在［a，b］内有二阶导数，则f（x）在［a，b］上为凸函数的充要条件是f″（x）≥0.

事实上，∀x1，x2∈R，α∈［0，1］，由于

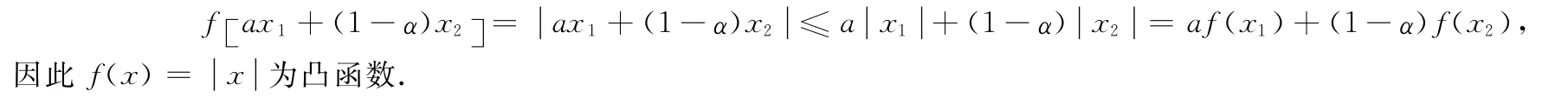
命题1 在应用凸函数的性质证明不等式时，应注意函数是否可导：（1）若未告诉f（x）二阶可导条件，则只能用定理1来证明相关不等式；（2）若告诉了f（x）二阶可导条件，则既可用定理1，也可用定理2来证明相关不等式.

下面通过实例来说明该问题.

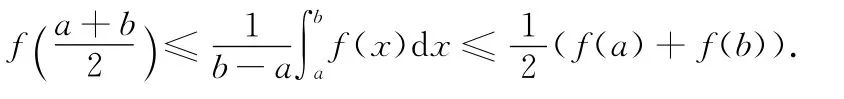
分析 由于这里f（x）虽然为凸函数，但是却未知f（x）二阶导数的相关信息，因此只能利用定理1来证明不等式.

证明 由f（x）为［a，b］上的凸函数，知f（x）在（a，b）内连续（换句话说，凸函数的不连续点只能在边界上.关于凸函数的更多性质，可以参考文献［4－5］），因此f（x）在（a，b）内可积.又因

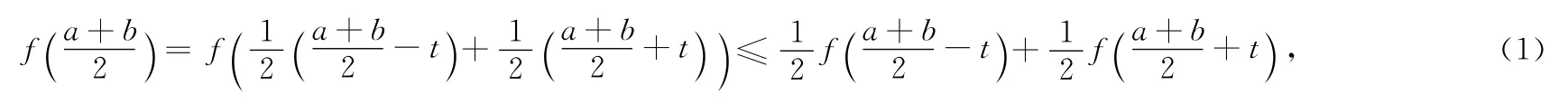
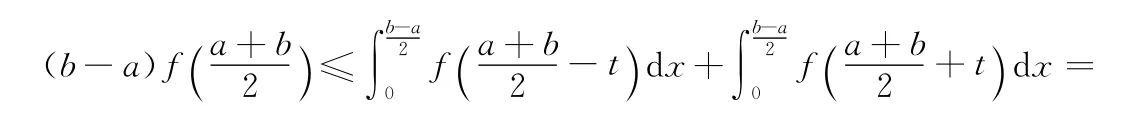
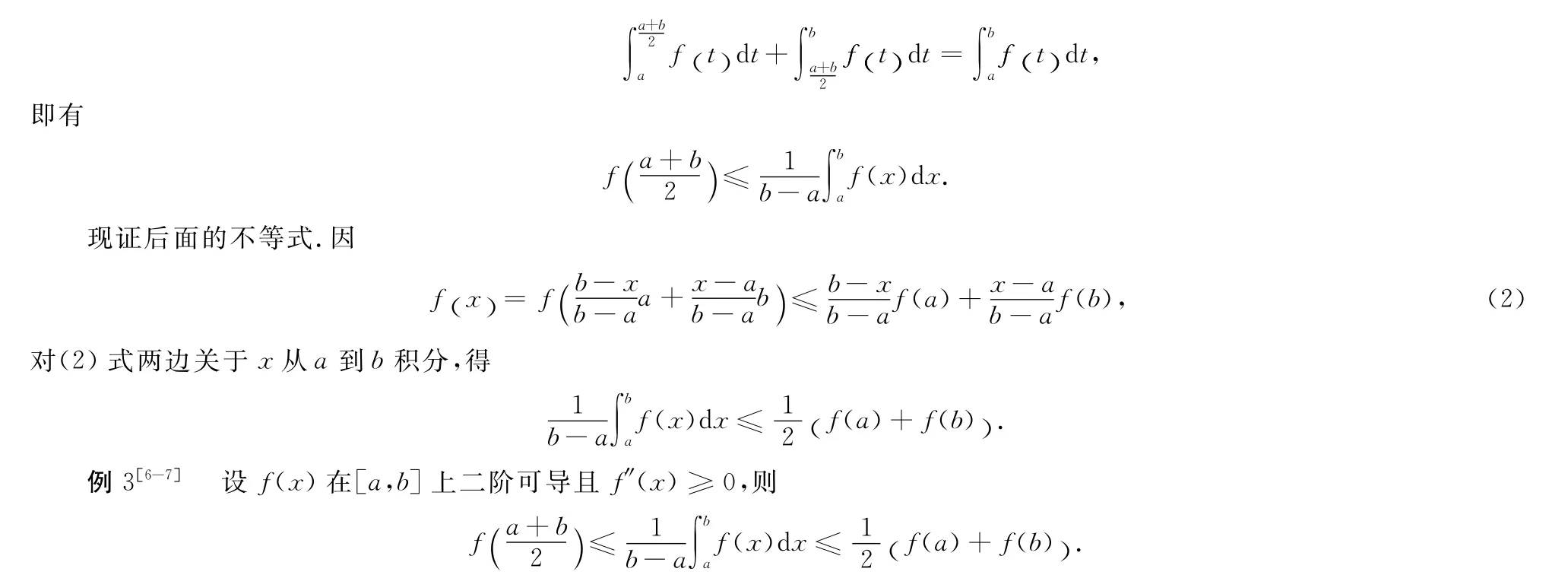
分析 由于这里告诉了f（x）二阶可导且f″（x）≥0，因此f（x）在［a，b］上为凸函数，故可用定理1来证明该不等式，方法如上.下面利用二阶导数存在且非负的性质来证明该不等式，作为对例2的补充.

证明 由于f（x）二阶导数存在，因此做f（x）在［a，b］中点处的二阶泰勒展式，有

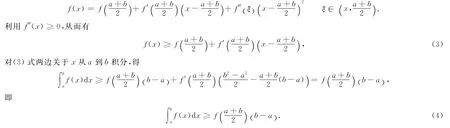
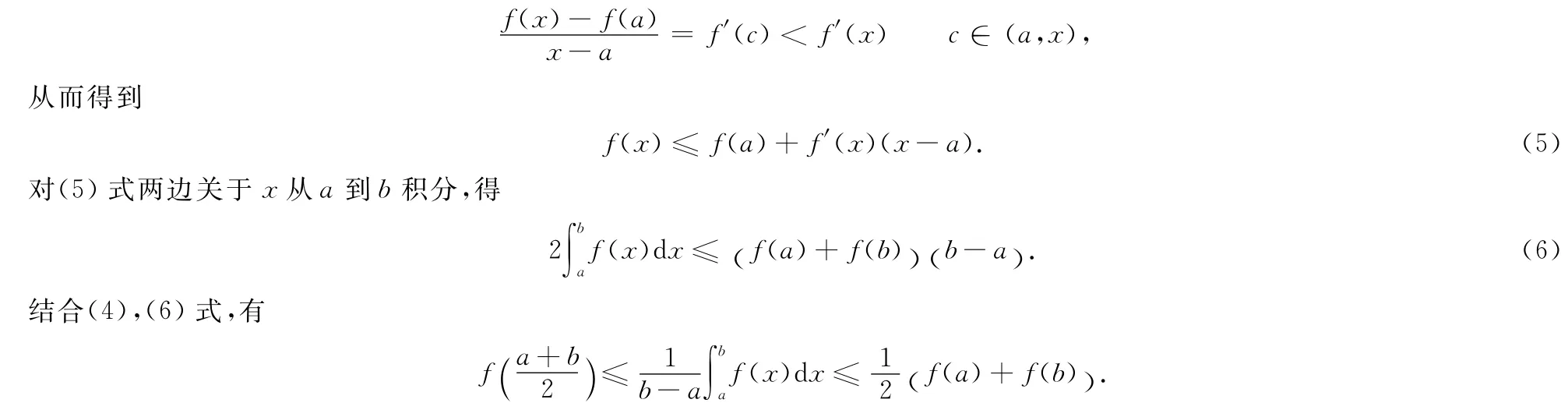
又因为f″（x）≥0，所以f′（x）在［a，b］上为单调递增函数.当a＜x＜b时，结合Lagrange中值定理有

关于如何利用凸函数的性质来证明不等式是微积分课程的一个重点和难点，鉴于该内容对学生进一步学习《泛函分析》、《凸分析》等课程具有重要的作用，笔者希望通过文中的几个例题使读者受到启发，使得读者在利用凸函数证明相关不等式时能够思路清晰，运用准确，少走弯路.下面利用凸函数来证明一个重要的不等式——康托洛维奇不等式（康托洛维奇不等式是优化理论中重要的不等式之一，它在许多方面都有重要应用），作为对命题1的一个应用.

定理3（康托洛维奇不等式） 设G为n×n的对称正定矩阵，其特征值为λ1≥λ2≥...≥λn，则对任何非0向量x∈Rn，总成立不等式

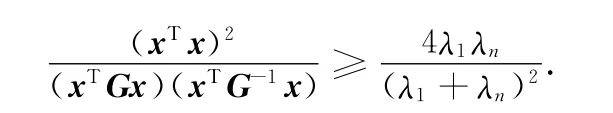
证明 由于G为n×n的对称正定矩阵，因此存在正交矩阵U，使得G＝UTΛU，其中Λ＝diag（λ1，λ2，...，λn）.做正交变换y＝Ux，得

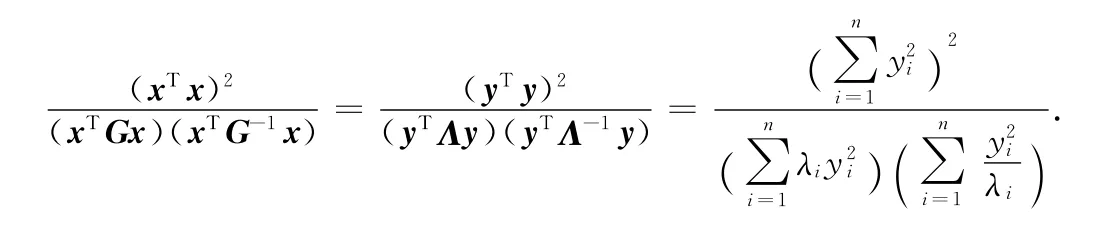
［1］ 陈传璋，金福临.数学分析［M］.第2版.北京：高等教育出版社，1983.

［2］ 陈开周.最优化计算方法［M］.西安：西安电子科技大学出版社，1985.

［3］ 胡 克.解析不等式的若干问题［M］.第2版.武汉：武汉大学出版社，2007.

［4］ 应玖茜，魏权龄.非线性规划及其理论［M］.北京：中国人民大学出版社，1994：53－61.

［5］ DIMITRI P BERTSEKAS.Convex Analysis and Optimization（英文影印版）［M］.北京：清华大学出版社，2000.

［6］ 贾建华，王克芬.微积分证明方法初析［M］.天津：南开大学出版社，1989.

［7］ 匡继昌.常用不等式［M］.第3版.济南：山东科学技术出版社，2004.

（责任编辑 向阳洁）

Two Notes on Proving Inequation by Using Convex Function

YONG Long－quan
（School of Mathematics and Computer Science，Shaanxi University of Technology，Hanzhong 723001，Shaanxi China）

Based on the distinguishing theorem for convex function，the author indicates some problems needing attention on proving inequation by using convex function：whether there exists second derivative is the starting point in proving some inequation.The author then proves the matrix form of Kantorovich inequation by using the property of convex function.

convex function；inequation；Kantorovich inequation

O178；O174.13

A

10.3969／j.issn.1007－2985.2013.06.004

1007－2985（2013）06－0012－03

2013－03－20

陕西省教育厅自然科学研究项目（12JK0863）

雍龙泉（1980－），男，陕西洋县人，陕西理工学院数学与计算机科学学院副教授，硕士，主要从事最优化算法研究.