Sierpinski垫上某类柯西变换的解析性*
2013-09-11李红光
李红光
(怀化学院数学系,湖南怀化 418008)
Sierpinski垫上某类柯西变换的解析性*
李红光
(怀化学院数学系,湖南怀化 418008)
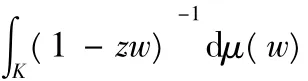
解析;Hausdorff测度;Sierpinski垫
1 问题的提出
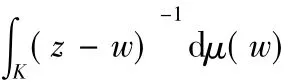

=∪2
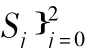
2 柯西变换的解析性

,则有a3k>0.
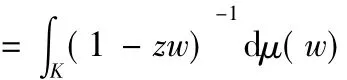

由(2)式和μ的旋转不变性,有
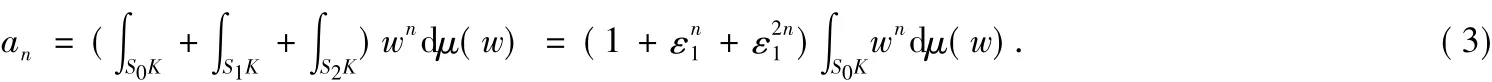
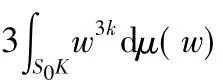
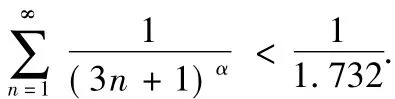
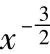
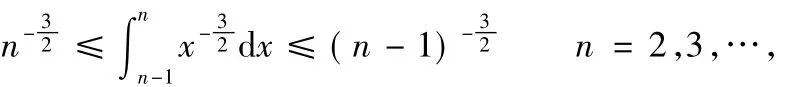
依次相加可得
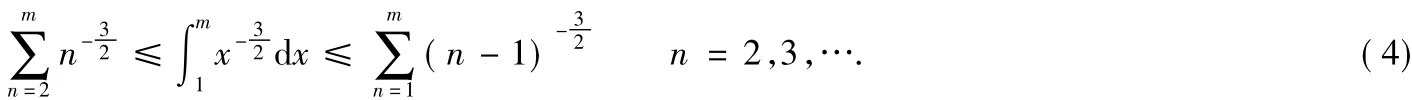
由(4)式左边,对任何正整数m,有
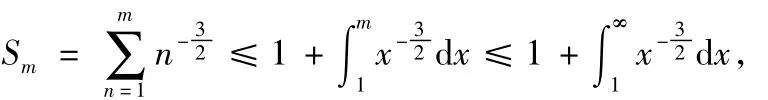
因此有

由文献[1]中定理5.6,有
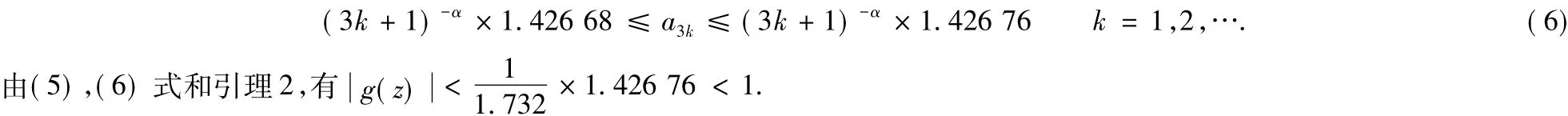
[1] DONG X H,LAU K S.Cauchy Transforms of Self-Similar Measures:The Laurent Coefficients[J].Funct.Anal.,2003,202: 67-97.
[2] HUTCHINSON J.Fractals and Self-Similarity[J].Indiana Univ.Math.,1981,30:713-747.
[3] FALCONER K J.Fractal Geometry-Mathematical Foundations and Applications[M].New York:John Wiley&Sons,1990:54 -65.
[4] 肯尼思·法尔科内.分形几何——数学基础及其应用[M].沈阳:东北大学出版社,1991:65-75.
(责任编辑 向阳洁)
Analytic Behavior of Certain Cauchy Transforms on Sierpinski Gasket
LI Hong-guang
(Department of Mathematics,Huaihua College,Huaihua 410008,Hunan China)
analytic;Hausdorff measure;Sierpinski gasket
O174.12
A
10.3969/j.issn.1007-2985.2013.01.004
1007-2985(2013)01-0014-02
2012-11-12
湖南省教育厅资助项目(11B095)
李红光(1979-),男,湖南新宁人,怀化学院数学系讲师,主要从事函数论研究.
