Liouville Type Theorem for a Parabolic Equation Involving Pucci Operato*

LIU Yong

(Department of Mathematics and Physics，North China Electric Power University，Beijing 102206，China)

Liouville Type Theorem for a Parabolic Equation Involving Pucci Operato*

LIU Yong

(Department of Mathematics and Physics，North China Electric Power University，Beijing 102206，China)

One classical result for the superlinear parabolic equation involving Laplacian operator is the Liouville type theorem.Due to the importance of these kind of theorems，the Liouville type theorem for parabolic equation involving Pucci’s operator is studied in this paper.When the space variable is one dimensional，it is relatively easy to analyze the Pucci operator.The main result of this paper states that in this case，the corresponding equation does not have global positive bounded solution.

Pucci operator;global solution;Liouville type theorem

1 Introduction

Consider the following parabolic equation:

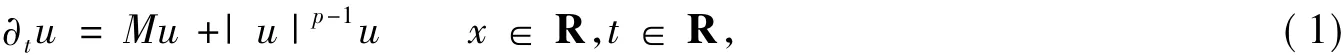
wherep＞1，Mis the Pucci operator given explicitly by

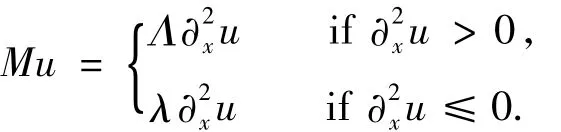
Here 0＜λ≤Λ are fixed constants.Note that the Pucci operator is a generalization of the Laplacian operator.Although it shares some similar properties with the Laplacian operator，in general，the Pucci operator is much more complicated.Recently，there is an increasing interest in the study of solutions to the fully nonlinear elliptic equation concerning this operator(for example see ref.［1-2］and the references t herein).

In this paper，we will prove a Liouville type result for the global solution of the equation(1).LetC2，1(R×R)be the space of functions which are twice continuously differentiable in the space variablexand once in the time variablet.Our main result is:

Theorem 1Supposep＞1.Then there is no positive boundC2，1(R×R)solution to the equation(1).

Several remarks are in order.If the Pucci operator is replaced by the Laplacian operator，and the space dimension isn≥1，then one could show the nonexistence of positive bounded radial solution if one assumes further thatpis superlinear and subcritical，namely，For a proof of this result，for example see ref.［3］.In our case，the Pucci operator is a fully nonlinear operator; therefore，if one would like to study(1)in any dimension，then techniques used in the Laplacian case should be modified.In particular，one should prove the so called zero number diminishing property for the corresponding equation.Fortunately，in dimension one，as we will see later，this difficulty could be somehow bypassed.This is the reason that we restrict to space dimension one in this paper，although one expects that similar results as theorem 1 should be true in any dimension.

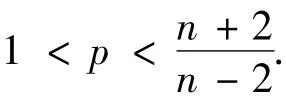
2 Proof of Theorem 1

In this section，as assumed in theorem 1，p＞1.Our method of proof will be a modification of that in ref.［3］for similar result in the Laplacian case.First of all，let us consider an elliptic version of(1).

Lemma 1There exists a function φ such that for eachr＞0，the onlyC2solution of

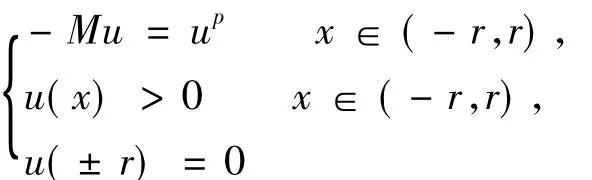
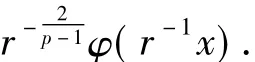
ProofBy the definition of the Pucci operator and the fact thatu＞0 in(-r，r)，we find thatu″(x)＜0 in (-r，r).ThereforeMureduces to λu″.The result then easily follows.

Using lemma 1，we could show the following:

Lemma 2There is no positive bounded global solution of

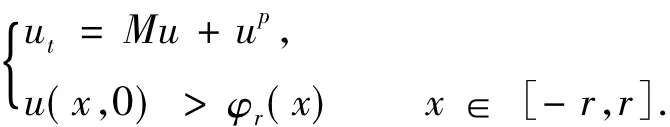
ProofSuppose to the contrary that such exists.

Sinceu(x，0)＞φr(x)forx∈［-r，r］，there existsc＞1 such thatu(x，0)＞cφr(x)，x∈［-r，r］.We know that

Therefore，by the comparison principle(for example see ref.［4］)，

On the other hand，by the a priori estimates，there is a sequence{ti}such thatu(·，ti)converges to a solution ξ ofMξ=ξpin(-r，r).This solution could be extended to a positive solution in some interval(-r1，r2)，which in addition vanishes on the boundary.This together with(2)contradicts with lemma 1.This completes the proof.

With these preparations，we are ready to prove our main theorem.

Proof of Theorem 1For anyr＞0 and functionf，letzr(f)be the number of zeroes of the functionfin the interval［-r，r］.

We first claim that for eacht∈R，zr(u(·，t)-φr(·))≥2.Otherwise，by lemma 2，we must havezr(u(·，t)-φr(·))=1.Hence for somex0∈(-r，r)and somet0，u(x0，t0)-φr(x0)=0，andu(x，t0)-φr(x)＞0 for other pointsxin［-r，r］.By lemma 2 again，one must have∂tu(x0，t0)≤0.This in turn implies that the Pucci operator reduces to the Laplacian operator in a neighborhood of(x0，t0).Then by the zero number diminishing property(see ref.［3］)，this could not happen.

Define

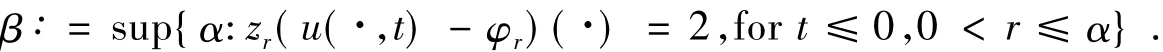
Note that forr＞0 small，by the boundedness ofu，we havezr(u(·，t)-φr(·))=2.Therefore β＞0 is well defined.

Next we show that β＜+∞.Indeed，forrlarge，φr(0)＜u(0，0).Now ifzr(u(·，t)-φr(·))=2 for allt≤0 with|t|small，then∂tu(x0，0)＜0.This in turn implies that(x0，0)＜0.Now in a small neighborhood of(x0，0)，the Pucci operator reduces to the Laplacian operator;therefore by the zero number diminishing property again，zr(u(·，t)-φr(·))≥4，fort＜0 small.This proves that β＜+∞.

Now let(tk，rk)be a sequence such thatrk→β andzrk(u(·，tk)-φrk(·))≥3.Then by the similar arguments as above，we could assumetk→-∞.Henceu(·，·+tk)→vin(R×R)，for some bounded functionvsolving(1).

Either the functionv(·，0)-φβ(·)has at least four nontrivial zeroes，or it has at least two nontrivial zeroes and one trivial zero，or it has at least two trivial zeroes.Here we say a pointx0is a trivial zero，if for eachx1＜x0＜x2，with|x1-x2|small，we have

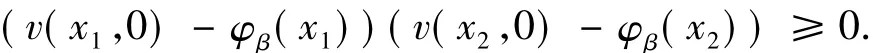
Then similarly as before，one could show that fort＜0 small，v(·，0)-φβ(·)has at least four nontrivial zeroes.By continuity，there existr＞β andt＜0 such thatzr(u(·，t)-φr(·))≥4，a contradiction.This completes the proof.

AcknowledgementThe author would like to thank Prof.P.Felmer for useful discussion.

［1］ FELMER P，QUASS A.Critical Exponents for Uniformly Elliptic Extremal Operators［J］.Indiana Univ.Math.J.，2006，55 (2):593-629.

［2］ FELMER P，QUASS A.On Critical Exponents for the Pucci’s Extremal Operators［J］.Ann.Inst.H.Poincaré，2003，20 (5):843-865.

［3］ QUITTNER P，SOUPLET P.Superlinear Parabolic Problems.Blow-up，Global Existence and Steady States［M］.Basel: Birkhauser Verlag，2007.

［4］ LIEBERMAN G M.Second Order Parabolic Differential Equations［M］.River Edge，NJ:World Scientific Publishing Co.，Inc.，1996.

(责任编辑 向阳洁)

关于Pucci算子的抛物方程的Liouville定理

刘勇
(华北电力大学数理学院，北京 102206)

关于含有Laplace算子的超线性抛物方程的一个经典结果是Liouville型的定理.由于这些定理在应用中的重要性，研究了关于Pucci算子的抛物方程的Liouville型定理.在空间变量为1维的情形下，Pucci算子的性质相对容易分析，对这一特殊情形，证明了对应的抛物方程没有全局有界的正解.

Pucci算子;全局解;Liouville型定理

O175.26

A

O175.26

A

10.3969/j.issn.1007-2985.2013.01.003

1007-2985(2013)01-0011-03

* Received date:2012-10-25

National Natural Science Foundation of China(11101141);Scientific Research Foundation for the Returned Overseas Chinese Scholars of the State Education Ministry;Doctoral Funding of North China Electric Power University

Biography:LIU Yong(1980-)，male，was born in Jiangying，Jiangsu Province，lecturer;main research areas are nonlinear analysis and nonlinear partial differential equations.