SturmLiouville算子特征值与特征函数更精确的估计＊

陈莉敏

（常州工程职业技术学院基础部，江苏常州 213164）

SturmLiouville算子特征值与特征函数更精确的估计＊

陈莉敏

（常州工程职业技术学院基础部，江苏常州 213164）

应用迭代法计算势函数光滑性提高时自伴型Sturm－Liouville算子特征值与特征函数的渐近估计式.

Sturm－Liouville算子；特征值；特征函数；估计

1 预备知识

对于Sturm－Liouville特征值问题Ly（x）＝－y″＋q（x）y＝λy，y′（0）－hy（0）＝0，y′（π）＋Hy（π）＝0，若q（x）∈Cm［0，π］，则特征值渐近式可表示为

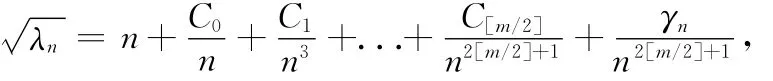
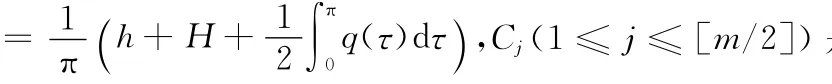
当势函数越来越光滑时，可将渐近式的表达式计算得更精确.但怎样确定估计式中的系数，没有文献给出具体的讨论.当q（x）∈C1［0，π］及q（x）∈C2［0，π］时，文献［4－6］分别给出算子特征值和特征函数的渐近式.笔者利用迭代法求解了q（x）∈C3［0，π］时算子特征值和特征函数的渐近展开式.

引理1［4］记λ＝s2，则

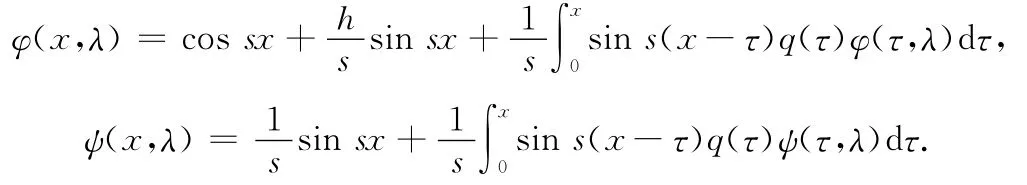
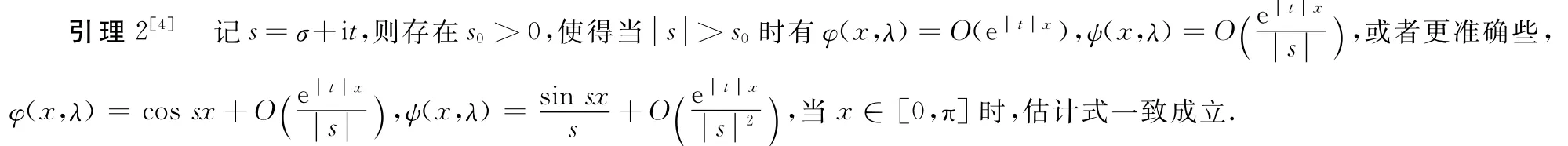
2 主要结果及其证明

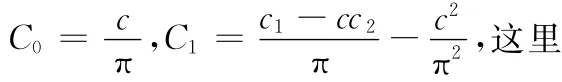
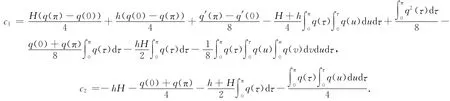
证明由引理2递推得

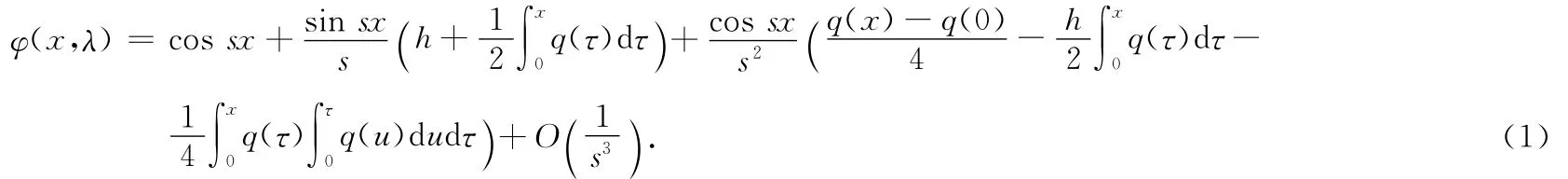
由边条件得（－s＋B）sin sπ＋Acos sπ＝0，其中

将（3）式带入（2）式，解得

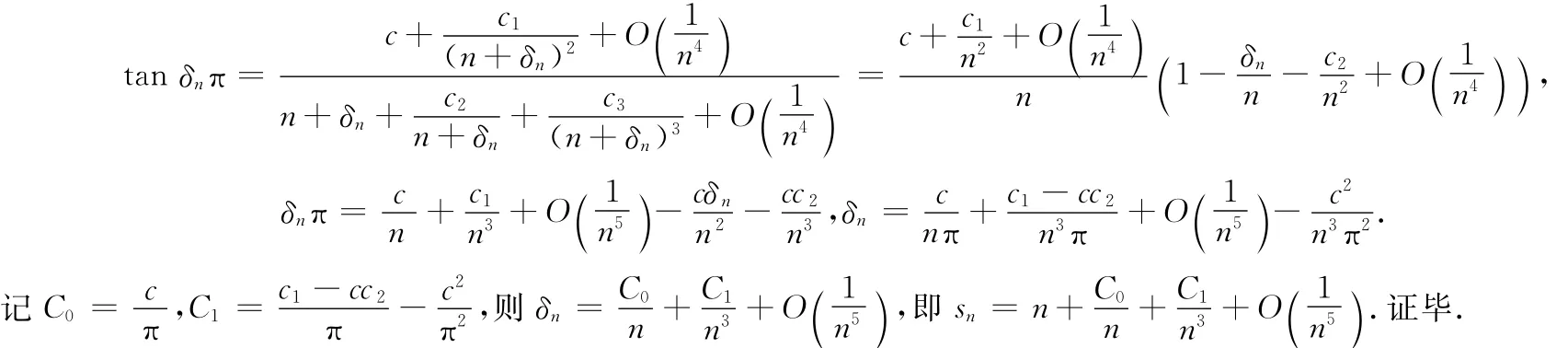
定理2 Sturm－Liouville算子在q（x）∈C3［0，π］时，特征函数的渐近式可表示为

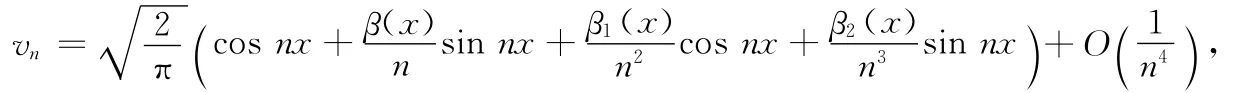
其中β（x），β1（x），β2（x）是与h，H，q（x）及其导数相关的实常数.

证明由引理2递推可得（1）式.

将定理1结论带入（1）式，得

［1］ ATKNSON F V.Discrete and Continuous Boundary Problems［M］.New York：Academic Press，1964.

［2］ EASTHAMM S P.On the Location of Spectral Concentration for Sturm－Liouville Problems with Rapidly Decayingpotential［J］.Mathematica，1998，45：23－36.

［3］ LEVITAN B M，SARGSJAN I S.Sturm－Liouville and Dirac Operators［M］.Dordrecht：Kluwer Academic Publishers，1991.

［4］ 刘景麟.常微分算子谱论［M］.北京：科学出版社，2009.

［5］ 陈莉敏.Sturm－Liouville算子特征值与特征函数的精确解［J］.佳木斯大学学报：自然科学版，2012（1）：155－157.

［6］ 陈莉敏.常型Sturm－Liouville算子特征值的渐近式和迹公式［J］.五邑大学学报：自然科学版，2012（5）：25－28.

（责任编辑 向阳洁）

Exact Estimation of the Eigenfunction and Eigenvalue for Sturm－Liouville Operator

CHEN Li－min
（Department of Basic Course，Changzhou Insititute of Engineering Technology，Changzhou 213164，Jiangsu China）

The expressions of the asymptotic formulae about the Sturm－Liouville operator are given by iterate algorithm.

Sturm－Liouville operators；eigenvalues；eigenfunction；estimation

O175

A

10.3969／j.issn.1007－2985.2013.03.003

1007－2985（2013）03－0012－03

2013－01－07

全国化工高职公共课教学指导委员会教科研课题（HGGJ1213）

陈莉敏（1977－），女，江苏扬州人，常州工程职业技术学院基础部讲师，硕士，主要从事微分方程研究.