基于混沌和取样积分技术的大型风电增速箱早期故障诊断

孙自强，陈长征，谷艳玲，刘 欢，2

(1.沈阳工业大学 机械工程学院，沈阳 110870;2.沈阳化工大学 信息工程学院，沈阳 110142)

风力发电机组增速箱作为变速传动机构，工作环境恶劣，传到齿轮的力相互耦合，长期在复杂的交变载荷下工作，齿轮断裂、粘合、齿轮轴点蚀、疲劳裂纹及滚动轴承损坏等故障时常发生。在整个风力机机械故障中增速箱故障率约为30%，由此引起的停机占比最大［1］。维修成本、时间成本均较高。对风力机增速箱早期故障检测极为重要。现有针对齿轮箱的分析方法有:时域波形分析、相关分析、功率谱分析、倒频谱分析等传统方法，以及小波分析、循环平稳理论、希尔伯特-黄变换等［2-5］。但风力机增速箱振动频率复杂，振动信号往往是突变及非平稳的，且微小故障信号易被周围强大振动源噪声干扰，导致故障信号信噪比低，难以提取，甚至难以扑捉。针对风力发电，目前尚缺乏有效的监测诊断方法，在线监测诊断系统尚为空白［6］。

本文提出基于混沌振子及取样积分技术对兆瓦级风电增速箱早期故障进行诊断。该技术充分利用duffing混沌振子对微弱周期信号敏感及对噪声免疫特点，待检微弱信号存在时，duffing混沌振子相图会产生突变。工程实践中为克服仅由相图变化而产生的主观错误，采用lyapunov指数进行定量判断，同时取样积分技术对时域信号进行预处理以提高混沌振子的检测门限。对某风场1.5 WM风力机增速箱实验结果表明，该技术能有效诊断风力机增速箱早期故障。

1 混沌振子对齿轮早期故障检测原理

1.1 混沌振子微弱信号检测

duffing振子特性研究较成熟。对Holmes型duffing振子，参数的微小改变会引起振动相图本质变化，方程式为:

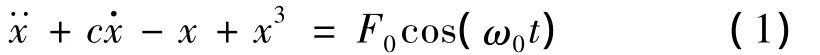
式中:c为阻尼系数;-x+x3为非线性恢复力;F0为振子内部摄动力幅值;ω0为角频率;x为混沌振子系统输出。当c，ω0等参数固定时，duffing振子状态会随F0增大，发生规律为同宿轨迹→分叉轨迹→混沌轨迹→临界周期→大尺度周期状态变化。通过对特定状态下混沌系统施加周期摄动力进行微扰，使系统由混沌状态突变到大尺度周期状态，从而根据系统相平面轨迹变化进行微弱信号检测［7-8］。图 1 为c=0.5，ω0=1，相图从混沌状态向大尺度状态的变化。

图1 duffing振子相图Fig.1 Phase portraits of duffing system

在风力机增速箱故障诊断中，设被检测微弱周期信号为F1cos(ω1t+θ)，其它外部噪声n(t)，故障特征频率ω1，相角为θ，式(1)改写成状态方程为:·

已知待检信号频率ω1时，令式(2)中内部摄动力频率ω0=ω1，可令F0略小于进入大周期尺度时的临界值Fb(可用Melnikov方法求解)。

齿轮单齿早期裂纹故障通过观察频谱图上齿轮啮合频率边频的增长进行判断。运用duffing混沌振子对啮合边频检测时，若边频带宽过小会受主频分量干扰而观察不到相图变化。李崇晟等［9］用混沌相图逆向变化解决此问题，即先令F0略大于Fb，ω0为主频分量频率，相图处于大周期尺度运动状态，若边频ω1幅值F1逐渐变大，与F0合力在Fb两侧变化，则会破坏原相图，重新进入混沌状态。

1.2 lyapunov指数

信噪比高的待检信号可通过相图直接观察到最终结果，但信噪比过低，仅观察相图进行判断较难确定。为定量判断增速箱是否存在早期故障，引入lyapunov指数。lyapunov指数是衡量系统动力学特性的重要定量指标，可表明系统在相空间中相邻轨道收敛或发散的平均指数率，是判断、描述非线性时间序列是否为混沌系统的重要参数，亦是区分系统处于混沌状态或非混沌状态的最直接特征量之一［10-11］。对二维相图，可记为:

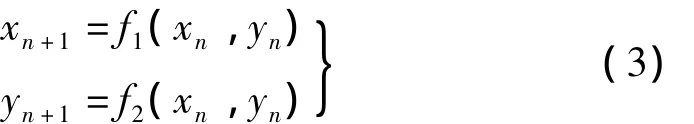
其Jacobi矩阵为:

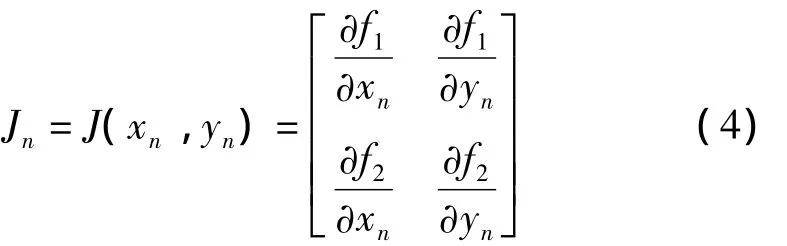
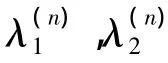
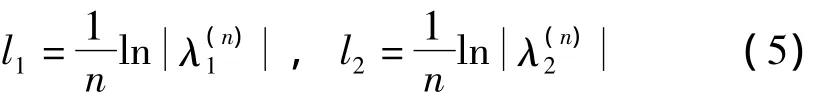
若最大lyapunov指数小于0，则相图发生大周期尺度变化，存在待检测信号;否则相图仍为混沌状态。图2为对图1不同状态相图的lyapunov指数谱计算，经约400次迭代，两个lyapunov指数趋于稳定。图2(a)最大lyapunov指数大于0，相图为混沌状态;图2(b)最大lyapunov指数小于0，可定量判断上述轨迹为大尺度周期运动，即存在待检信号。

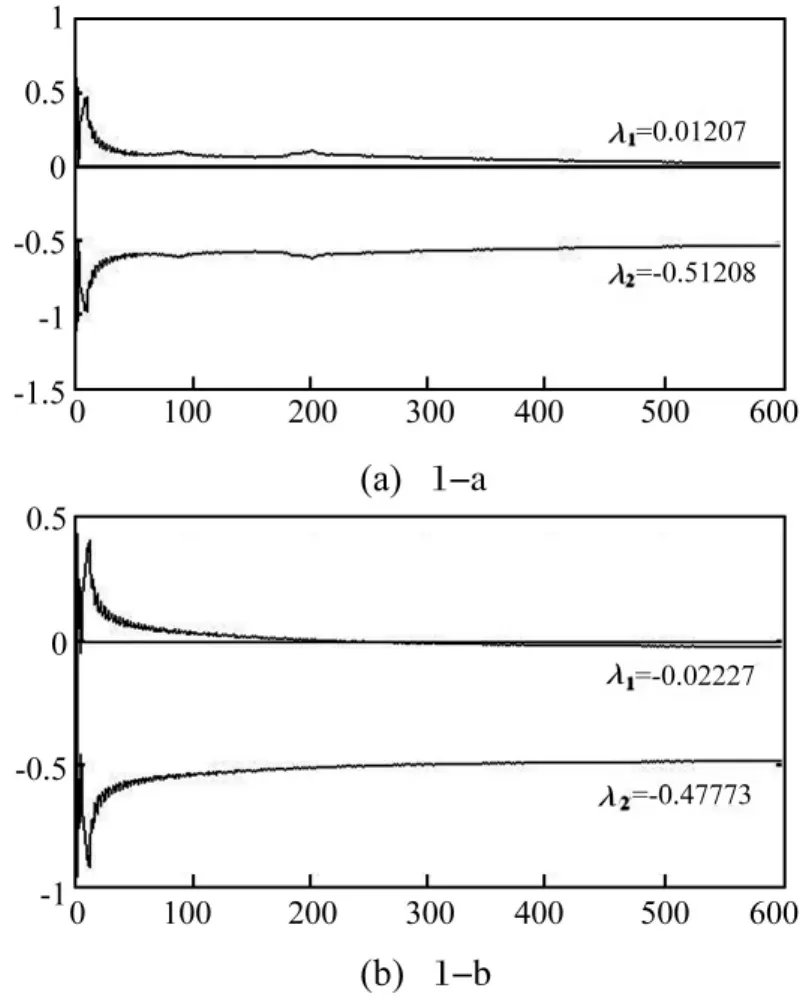
图2 lyapunov指数谱Fig.2 lyapunov exponents spectrum

2 增速箱振动信号取样积分降噪

非线性混沌振子对微弱信号检测有很大优点，而传统的线性检测技术采用噪声抑制方法。若在微弱信号提取前，先抑制噪声则可大大提高混沌振子检测门限［12］。对淹没在噪声中的故障信号进行等间隔采样，保证对某个轴不同时刻采集的信号起始点相位一致，采样频率与采样点数相同，对该时域信号进行平均，能大大提高信噪比，此方法称为取样积分。设待检信号为s(t)，噪声信号n(t)，取样周期为T，经N次积累平均，输出为:

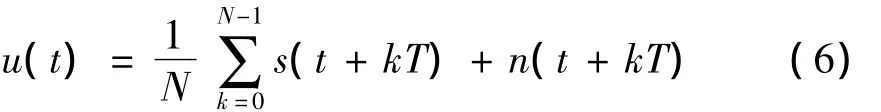
对于白噪声，当N足够大，输出可以认为是:

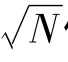
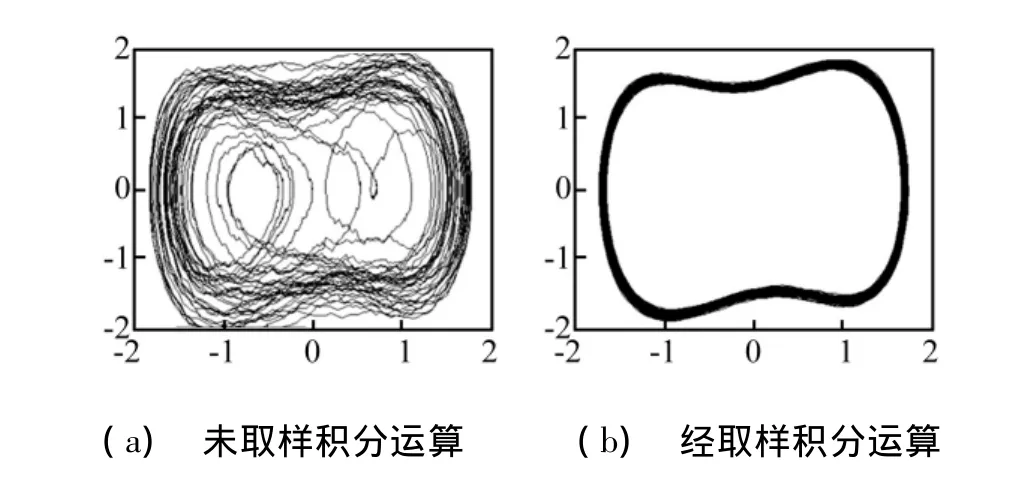
图3 采用取样积分前后进行混沌检测的相图Fig.3 Phase portraits with and without sampling integral

3 增速箱振动信号分析

3.1 信号检测

风力机增速箱中齿轮故障包括断齿、齿面疲劳、胶合等。齿轮振动信号包含齿轮啮合基频及各阶谐波，以及幅值较低、以齿轮各阶啮合谐波为中心、以齿轮转频为宽度的调制边频带。因此，在野外恶劣环境下齿轮传动过程中反复受交变载荷作用，齿轮均匀磨损性能退化或出现单齿缺陷后，应及时维修，以免造成大故障。

齿轮不均匀裂纹形成及发展过程中，齿轮啮合频率被旋转及其它设备频率所调制，裂纹发展在频谱图上表现为齿轮啮合基频边频的增长。可通过监测边频变化确定齿轮裂纹的发展状态。对风电机组边频带间距过小，尤其几种故障并存时，边频族错综复杂，成分不稳定，且存在两个轴旋转频率混合情况。由式(2)对边频信号检测，混沌振子会受主频强烈干扰。式(2)中内置信号ω0设为啮合频率，总策动力表达为［13］:

式中:

Δω很小时，F(t)将在F0-F1与F0+F1之间变化。若F0较临界值Fb略大，相图将在大尺度周期与混沌状态交替变化。利用混沌振子相图逆向检测啮合频率边频带变化可判断齿轮裂纹是否存在。

齿轮均匀磨损表现为齿轮啮合频率及谐波幅值明显增大，且幅值增大幅度随阶数增大而增大。风力机增速箱齿轮正常工作时，啮合频率三次谐波幅值不高，受调制及其它噪声干扰，在频谱分析中较难发现。可通过混沌振子正向检测该频率信号是否存在作为齿轮性能退化依据，将式(2)中内置信号ω0设为三次谐波频率对齿轮均匀磨损状态进行检测。

对齿轮裂纹与均匀磨损两类故障特征信号分别取样积分预处理后，信号噪声得到一定程度抑制，再分别进行混沌振子逆向、正向检测，信号提取见图4。

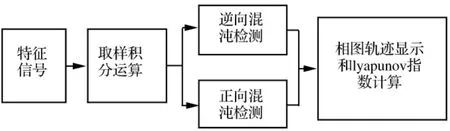
图4 信号检测过程Fig.4 Signal extracting process

3.2 实验分析

对内蒙某风场同型号1.5WM大型风力机组增速箱运行状态进行长期实验观察，在增速箱输入、输出端安装加速度传感器。机组增速箱内部结构与传感器安放位置示意图见图5。

图5 增速箱结构与传感器分布示意图Fig.5 Structural diagram of gearbox and sensors distribution

该增速箱由一级行星齿轮传动与两级平行齿轮传动构成。风场每日定期记录增速箱四个测点的振动数据。观察过程中某一机组增速箱突然有“咔咔”的冲击声，出现故障，停机维修。发现增速箱输入端小齿轮Z2断齿严重。为此，选该机组四个月前低速端径向振动信号作为正常参考信号，对故障出现8周前、4周前、1周前振动信号用上述方法进行分析比较。由转速及各齿轮啮合情况，求出额定转速下输入端齿轮的啮合频率为 52.32 Hz，二倍频 104.64 Hz，三倍频 156.96 Hz。图6为该机组正常工作、事故发生前8周、4周及1周前振动信号滤波后的归一化频谱图。由图6(b)、(c)对齿轮工作状态不易判断，而图6(d)频谱图啮合频率及边频带变化较明显。四组状态分别对啮合频率边频进行逆向混沌振子检测及啮合频率三倍频正向混沌振子检测。检测前先对时域信号进行取样积分降噪，提高检测门限，结果见图7、图8。不同检测过程的duffing混沌振子内部摄动力F0幅值可分别通过小步进取值方法求得，即正常机组运行状态下采样时间序列数据发生大尺度周期变化的临界值。

图6 振动频谱分析Fig.6 Frequent domain analysis

图7 基频边频带混沌检测Fig.7 Sideband signals detected by chaotic oscillator

图8 三倍频混沌检测Fig.8 Third harmonic signals detected by chaotic oscillator

由齿轮裂纹故障检测实验得F0=0.432，ω0=52.32 Hz时，正常工作的振动信号经过duffing混沌振子检测，相图处于大周期尺度状态，见图7(a)。齿轮正常工作时，齿轮啮合频率fr与其它边频带相比幅值较高，对混沌振子产生主要影响，故式(9)中总策动力F(t)幅值始终大于大周期尺度的临界值Fb，duffing振子相图即处于大尺度周期状态。随齿轮裂纹的产生，裂纹特征频率对啮合频率调制，啮合频率分量相对减少;边频带幅值变大，对混沌振子影响亦越主要，总策动力F(t)幅值在临界值Fb上下波动，相图状态发生变化，由最初的大尺度周期状态退化为混沌状态，见图7(b)、(c)，由此可判断齿轮产生初步裂纹。随齿轮裂纹的加深出现断齿，大量周期振动对振子产生深刻影响，图7(d)为产生大周期及混沌交替变化的相图，相图轨迹更多集中在大尺度周期上，间或进入混沌状态。

进行齿轮均匀磨损状态监测时，混沌振子内置频率为 ω0=156.96Hz;幅值F0=0.826时，正常工作下对啮合频率三倍谐波进行混沌检测。齿轮啮合频率3倍频相对较小，对时域信号取样积分运算后经混沌振子正向检测仍不能检测出该信号，相图处于混沌状态，见图8(a)。对振动信号16周、8周、2周前啮合频率三倍谐波进行混沌振子正向观察，检测齿轮磨损情况。随着齿轮磨损，三倍频幅值增大，总策动力幅值超过临界值Fb，观察图8(b)发现振子出现相图变化，在16周前提示此时齿轮已有一定程度磨损，相图进入临界混沌状态。图8(c)相图完全进入大尺度周期运动状态，提示齿轮磨损进一步加剧，三倍频幅值可被清晰检测出来。经计算，四种状态最大 lyapunov指数分别为1.246 2，-0.016，-1.635，0.301。从指数看，随着磨损的加剧三倍频幅值增大，检测出信号，相图从混沌状态进入周期运动，但齿轮裂纹严重时，由于边频信号干扰，相图8(d)又重回混沌状态。因为此时齿轮裂纹故障可能已较严重，三倍频边频对相图产生显著影响，需进一步检查分析。总之，齿轮随着磨损的加剧，duffing混沌相图为从混沌状态→大尺度周期状态→混沌状态的变化过程。由此可定性判断齿轮磨损变化，而从FFT谱图较难看出明显变化。

4 结论

(1)利用混沌振子与取样积分技术对增速箱振动信号进行检测，通过线性降噪提高了非线性混沌振子从噪声中提取微弱信号的能力，对噪声抑制较好，且信噪比工作门限较低。

(2)分别对增速箱齿轮裂纹啮合频率边频带采用逆向混沌振子与对齿轮均匀磨损状态特征频率三倍频采用混沌振子正向检测手段，对风力机增速箱早期故障进行实验研究表明，借助lyapunov指数定量分析，克服了对故障判断的主观性，对早期故障能较好识别，具有工程应用价值，为风力机增速箱早期故障检测的新方法。

(3)采用同样方法也可对其它动齿轮、轴及轴承进行检测，以及时发现问题，避免风力机事故发生。

［1］Amirat Y，Benbouzid M E H.A brief status on condition monitoring and fault diagnosis in wind energy conversion systems［J］.Renewable and Sustainable Energy Reviews，2009，13(9):2629-2636.

［2］ Hameeda Z，Honga Y S.Condition monitoring and fault detection of wind turbines and related algorithms:a review［J］.Renewable and Sustainable Energy Reviews，2009，13(1):1-13.

［3］陈长征，梁树民.兆瓦级风力发电机故障诊断［J］.沈阳工业大学学报，2009，31(3):277-280.

CHEN Chang-zheng，LIANG Shu-min.Fault diagnosis for megawatt wind generator［J］.Journal of Shenyang University of Technology，2009，31(3):277-280.

［4］何创新，李彦明，刘成良，等.基于滑动平均与相关向量机的齿轮早期故障智能诊断［J］.振动与冲击，2010，29(12):89-92.

HE Chuang-xin，LIYan-ming，LIU Cheng-liang，etal.Incipient faultdiagnosisbased on movingaverage and relevance vector machine［J］.Journal of Vibration and Shock，2010，29(12):89-92.

［5］盛迎新，周继威.风电机组在线振动监测系统及现场应用［J］.振动、测试与诊断，2010，30(6):703-705.

SHENG Ying-xin， ZHOU Ji-wei. Mems-based attitude measurement system for miniature air vehicle［J］.Journal of Vibration，M easurement ＆ Diagnosis，2010，30(6):703-705.

［6］陈雪峰，李继猛，程 航，等.风力发电机状态监测和故障诊断技术的研究与进展［J］.机械工程学报，2011，47(9):45-50.

CHEN Xue-feng，LI Ji-meng，CHENG Hang，et al.Research and application of condition monitoring and fault diagnosis technology in wind turbines［J］.Journal of Mechanical Engineering，2011，47(9):45-50.

［7］胥永刚，马海龙，付 胜，等.机电设备早期故障微弱信号的非线性检测方法及工程应用［J］.振动工程学报，2011，24(5):529-536.

XU Yong-gang，MA Hai-long，FU Sheng，et al.Theory and applications of weak signal non-linear detection method for incipient fault diagnosis of mechanical equipments［J］.Journal of Vibration Engineering，2011，24(5):529-536.

［8］ Guanyu W，Dajun C，Jianya L，et al.The application of chaotic oscillators to weak signal detection［J］.IEEE Trans.On Industrial Electronics，1999，46(2):440-444.

［9］李崇晟，屈梁生.齿轮早期疲劳裂纹的混沌检测方法［J］.机械工程学报，2005，41(8):195-198.

LI Chong-sheng，QU Linng-sheng.Chaotic detection method of gear early stage fatigue crack［J］.Chinese Journal of Mechanical Engineering，2005，41(8):195-198.

［10］ Kantz H.A robust method to estimate the maximal lyapunov exponent of a time series［J］.Physics Letters A，1994，185(1):77-87.

［11］ Yang C，Wu C Q.A robust method on estimation of lyapunov exponents from a noisy time series［J］.Nonlinear Dynamics，2011，64(3):279-292.

［12］姜卓娇，于生宝，白 毅，等.基于取样积分技术的数据采集系统［J］.吉林大学学报，2007，25(3):232-237.

JIANG Zhuo-jiao，YU Sheng-bao，BAI Yi，et al. Data collecting system based on sampling integral technology［J］.Journal of Jilin University，2007，25(3):232-237.

［13］李舜酩，李香莲.振动信号的现代分析技术与应用［M］.北京:国防工业出版社，2008:312-316.