铝蜂窝串联缓冲结构静态压缩仿真与试验研究

李 萌，刘荣强，罗昌杰，郭宏伟，丁北辰

(1.哈尔滨工业大学 机电工程学院，哈尔滨 150080;2.中国科学院深圳先进技术研究院，深圳 518000)

多孔固体结构作为一种兼具功能和结构双重属性的材料结构，近年来得到迅速发展。铝蜂窝作为多孔固体结构的一种，因其具有密度小、刚度低、压缩变形大及变形可控以及可缓冲吸能、制造工艺成熟等优点得以广泛应用［1-5］。铝蜂窝缓冲器在航天着陆器中可吸收着陆冲击能量。其典型应用实例即成功登陆月球的阿波罗11号着陆器。铝蜂窝缓冲器的缓冲特性与其箔材的材料、厚度、芯格尺寸、相对密度及拓扑结构有关，这些参数受环境影响较小，缓冲性能稳定［4-13］。

受加工工艺限制，国外只有宽度600 mm铝箔。国内铝箔最大宽度300 mm。故铝蜂窝最大轴向高度为600 mm，考虑到安全性及对着陆器承载能力要求，设计着陆腿时其行程须大于600 mm。目前现有铝蜂窝均不能满足设计需求。为此各国采用多级组合式缓冲方式，不但解决了铝泊长度受限问题，亦提高了着陆器软着陆过程中的稳定性及吸能效率。Yasui［7］通过试验对A5052，A6451-T6，A6451-T4三种不同基体材料的铝蜂窝进行冲击试验研究，提出金子塔形组合式缓冲结构，并对其进行了试验研究，发现多层组合蜂窝结构在每层蜂窝达到应力极限后产生压溃，且2层或3层金字塔形结构蜂窝能量吸收能力较好，认为金字塔形结构与同一尺寸多层结构组合会产生更高性能的缓冲器。国内对串联式蜂窝缓冲器研究较少，本文通过仿真与试验对串联式蜂窝缓冲器受压缩载荷作用进行研究，可为着陆器用串联蜂窝缓冲器设计提供技术支持。

1 蜂窝结构异面吸能特性

蜂窝结构因其结构特性，在不同方向外力作用下会产生不同的力学响应。当蜂窝材料受z轴方向压缩载荷作用时(图1)，称为异面压缩;而当压缩载荷加载方向处于x，y平面内时，称为面内加载。据文献［14］，铝蜂窝材料的异面平均应力远大于面内平均应力。因此，作为缓冲器，蜂窝材料通常承受异面方向载荷，本文主要研究异面压缩载荷作用下铝蜂窝串联结构的吸能特性。

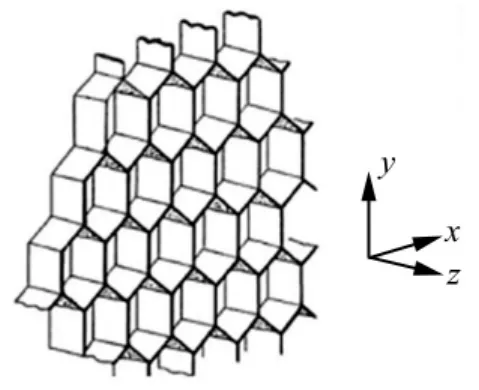
图1 铝蜂窝材料异面示意图Fig.1 Principal schematic of honeycomb material’s out-of-plane direction

弹塑性蜂窝材料变形过程［14］可描述为:① 压缩的初始阶段，蜂窝材料在载荷作用下首先发生弹性屈曲;② 随着压缩的进行，蜂窝材料发生塑性坍塌;③ 在大压力作用下，蜂窝材料孔穴的相对壁面压实在一起，且孔壁材料本身也被压缩，应力-应变曲线会陡然上升。典型弹塑性蜂窝材料在异面压缩下的应力-应变曲线图见图2。其变形过程可分为:初始阶段的弹性变形段，稳态塑性压溃段及压实段。

1.1 弹性变形段

对弹塑性蜂窝材料，开始加载时，孔壁将产生弯曲，在载荷未达屈服强度之前，应力表现出随应变线性增长趋势，即线弹性变形段。线弹性阶段的结束通常因胞壁发生弹性屈曲。此时的应力对应于应力-应变曲线中峰值应力。

1.2 稳态塑性压溃段

当垂直z向的截面应力超过孔壁材料屈服强度时，孔壁将产生轴向屈曲，进而发生塑性坍塌，此时压缩应力对应为平均应力。蜂窝材料吸能的有效阶段即此阶段。

1.3 压实段

孔壁因塑性坍塌而产生接触并堆积到一起，继续变形会压缩到堆积孔壁材料本身，并使之压实，导致最后阶段的应力-应变曲线陡然上升。压实段所对应的变形量表征了蜂窝材料变形能力，应变为蜂窝材料的极限应变εm。

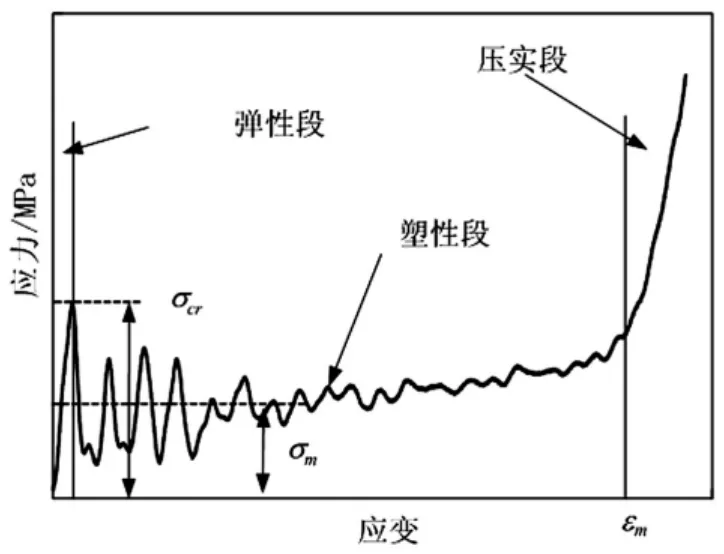
图2 蜂窝受异面压缩载荷作用典型应力-应变曲线图Fig.2 Typical stress-stain curve of honeycomb under out-of-plane impact load

2 串联蜂窝缓冲器应用

成功登陆月球的阿波罗系列着陆器为典型腿式月球着陆器(图3)，该着陆器具有四条主着陆腿及八条辅助着陆腿，每个着陆腿内填充铝蜂窝缓冲器。

该着陆器主着陆腿为圆形套筒结构，见图4。主着陆腿内径140 mm，着陆腿可压缩行程812 mm，此两数值限定了蜂窝缓冲结构的外形尺寸。

图3 阿波罗11号着陆器Fig.3 Apollo 11 lander

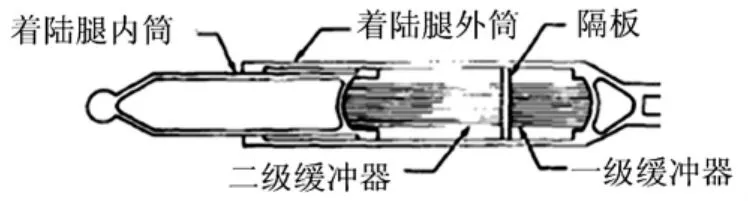
图4 阿波罗11号着陆器主着陆腿结构示意图Fig.4 Apollo 11 landing-gear primary strut

在设计月球腿式着陆器用缓冲器时需考虑两种特殊着陆工况:① 理想着陆工况，如图5(a)所示。该工况假定着陆环境较平坦，且垂直着陆速度最低，水平着陆速度为零，着陆时四个主着陆腿同时与月球面接触，着陆腿内部缓冲器同时作用共同吸收能量，此工况缓冲器吸收能量最少;② 着陆极限工况，如图5(b)所示。该工况着陆时单个着陆腿先与月球表面接触，为保证实验设备不受损坏，缓冲器设计要求单个主着陆腿缓冲器吸收全部着陆时的动能及势能。考虑到月球表面着陆环境及着陆姿态等因素，为更有利保证着陆器软着陆时所搭载的实验设备受冲击力最小，NASA对主着陆腿内缓冲器进行了串联处理，其中一级铝蜂窝缓冲器强度较弱，用于吸收理想着陆情况下着陆器全部能量，二级铝蜂窝缓冲器强度较强，单腿内一级缓冲器与二级缓冲器组合以吸收极限工况下着陆器着陆过程的全部能量。

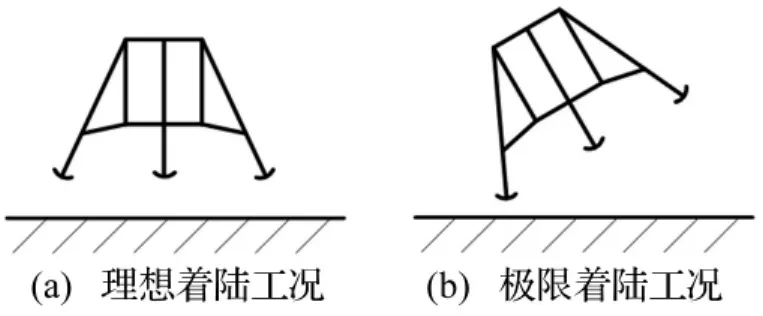
图5 两种特殊着陆姿态示意图Fig.5 Sketch of lander two special landing attitude

3 数值仿真

仿真用铝蜂窝结构有多种规格，其建模涉及参数较多，包括制造铝蜂窝材料的箔材厚度、试件高度、材料相关参数及胞元边长等参数。对每种不同规格的铝蜂窝手动建模有大量重复工作，势必浪费很多时间。若通过编写参数化程序实现对整个过程的参数化建模，每次只需在程序中输入主要参数，即能够实现自动建模、自动加载分析条件，可极大节省时间、提高工作效率，获得事半功倍效果。本文用MSC.Patran提供的PCL语言编写参数化程序，可实现串联式铝蜂窝缓冲器三维模型自动建立、网格自动划分及边界条件自动加载，且开发的人机界面友好、方便使用，提高仿真效率。整个参数化建模分析过程无须人工干预，减少了人为错误的产生。该程序操作界面如图6所示。

图6 参数化程序用户界面Fig.6 The interface of parametric program

本文将MSC.Patran软件用于前处理，将LS-Dyna软件用于求解分析。串联式铝蜂窝缓冲器三维模型如图7所示。分析模型置于两刚性平板之间，其中底层刚性平板完全固定，模拟准静态压缩过程中的支撑平台，上层刚性平板以恒定速度下落，对分析模型进行压缩，模拟准静态压缩过程中的压头。在两级铝蜂窝缓冲器中加入刚性平板模拟缓冲器之间的刚性隔板。为防止在压缩过程中因蜂窝结构发生屈曲，使模型各面之间产生接触发生穿透现象，在选择接触类型时，选通用的单面接触和自动接触，设置自动接触后，在壳单元的两侧会产生接触限制。为模拟铝蜂窝自身的摩擦和铝蜂窝与刚性隔板之间的摩擦，在接触算法中设置铝蜂窝自身接触摩擦系数为0.1，设置铝蜂窝与刚性隔板之间的摩擦系数为0.17。为保证仿真结果有足够精度，每个单元边长分布有十个Belytschko-Tsay型壳单元，用面内单点积分，计算速度快，对大变形问题为最稳定有效的计算式［15］。

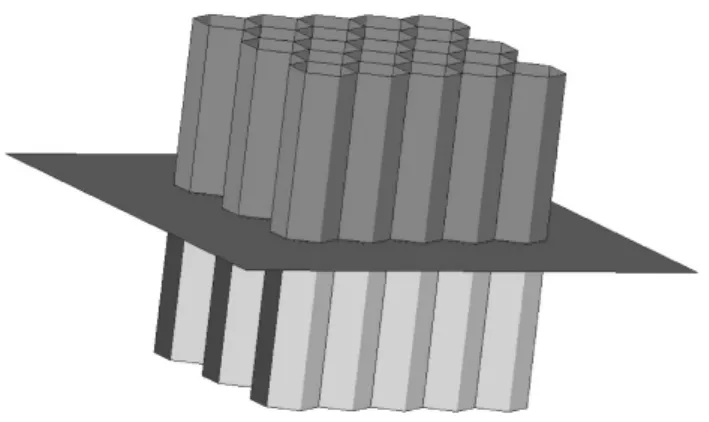
图7 串联式铝蜂窝缓冲结构三维模型图Fig.7 The 3D map of series honeycomb structures

用于制造铝蜂窝的铝箔材料通常有2024、3003、5A02、5A06、5052及5056等，其中3003的加工性能好、成本较低，但其强度较低，5056的强度最高，但其加工性能较差，成本较高。具体采用何种基体材料的铝蜂窝，需根据设计条件选择。本文选3003H18为研究对象，对不同规格的铝蜂窝试件进行准静态压缩仿真。由于铝蜂窝材料塑性好，且为准静态压缩模拟，故不考虑材料应变率敏感问题，将其视为理想弹塑性材料。用Elastoplastic-Plastic Kinematic(MAT3)材料模型模拟铝合金3003H18铝蜂窝基体材料。仿真用材料参数见表1。为使研究不受蜂窝外形尺寸限制，本文采用应力-应变曲线方式对蜂窝压缩特性进行研究。应力由蜂窝所受载荷与蜂窝横截面积相除得到，同样应变由蜂窝压缩行程除以蜂窝原有高度得到。文献［16-20］证明用该方法对蜂窝受异面压缩载荷作用的响应分析，不受蜂窝外形尺寸影响。

仿真中单个铝蜂窝模型编号由四个字符组成，第一，二位数字“xx”，表示胞元厚度为0.xx mm。第三，四位上的数字“xx”代表胞元边长，mm;如0604，表示铝蜂窝模型规格胞元厚度0.06 mm，胞元边长4 mm的铝蜂窝。

表1 铝蜂窝基体材料参数Tab.1 Parameters of aluminum honeycomb basis material

图8(a)为规格不同的铝蜂窝串联压缩仿真变形过程应力云图(0604-0504)。从整个变形过程可看出，串联铝蜂窝缓冲结构较弱一级先变形，发生屈曲;而强度较高一级则未进入屈服状态，待第一级完全压实后且压缩应力达到第二级铝蜂窝峰值应力时二级铝蜂窝进入屈服状态，以塑性变形吸收整个压缩过程能量。图8(b)为相同规格铝蜂窝串联压缩仿真变形过程的应力云图(0604-0604)。该图表明同种规格的串联铝蜂窝缓冲结构受轴向载荷压缩时，由于上下两级铝蜂窝规格相同，两级蜂窝同时进入屈服阶段，通过塑性坍塌吸收能量。

图8 两种仿真变形过程云图Fig.8 Two deformation process of series honeycomb structures

4 试验

为验证仿真模型的准确性，进行六组试验，分别为相同规格串联及不同规格串联铝蜂窝缓冲结构的压缩试验。所有试验均在室温23℃、相对湿度50%条件下进行，采用Instron 5569标准电子万能拉伸试验机，压缩方向为轴向，并取稳态压缩速度50 mm/min。对串联铝蜂窝压缩试验，以编号0608-0604的试验组合为例，代表单件试件规格0608和0604的铝蜂窝试件串联组合。六次试验编号分别为0608-0604、0508-0708、0604-0805、0604-0504、0604-0604、0805-0805。

因商用铝蜂窝均为蜂窝板，为保证实验具有较好的可重复性，同时考虑试验机最大试件尺寸限制，采用线切割加工方式获得。试验表明，切割后试件边缘齐整，一致性较好，能满足实验要求。实验用铝蜂窝试件胞元均为正六边形结构。试验中将串联铝蜂窝缓冲结构置于压缩机中间，为防止铝蜂窝彼此间的相互侵入，在两层铝蜂窝间加入隔板。整个试验装置见图9。

为增加试验的可靠性，对每组试验重复三次，平均应力值与极限应变值取三次试验平均值，由试验分析发现每组三次试验偏差最大不超5%，证明了试验的可靠性。

对不同规格的串联铝蜂窝缓冲结构压缩试验，在试验中上层压头对铝蜂窝缓冲结构进行压缩，串联铝蜂窝缓冲结构中强度较弱的铝蜂窝先进入屈服阶段，该铝蜂窝压缩过程接近完成时，即进入密实化阶段后，铝蜂窝缓冲结构受到载荷急剧增大，当压缩载荷达到另一级铝蜂窝缓冲结构的峰值力时，下层铝蜂窝开始变形，进入压缩载荷稳定的塑性坍塌阶段，当下层铝蜂窝缓冲结构进入密实化阶段后，整个串联组合受到的压缩载荷会急剧上升。

图9 铝蜂窝串联组合压缩试验装置图Fig.9 Experimental instrument of series honeycomb structures with compression

串联铝蜂窝缓冲结构由不同规格铝蜂窝组成，见图10。由应力-应变曲线可见，不同规格串联铝蜂窝结构出现2个较大的应力峰值，分别为单级铝蜂窝缓冲结构峰值应力。2个较明显的应力平台阶段为单级铝蜂窝缓冲结构的塑性坍塌阶段，在此阶段铝蜂窝通过蜂窝壁的塑性叠缩吸收能量，是铝蜂窝缓冲结构的主要吸能阶段。

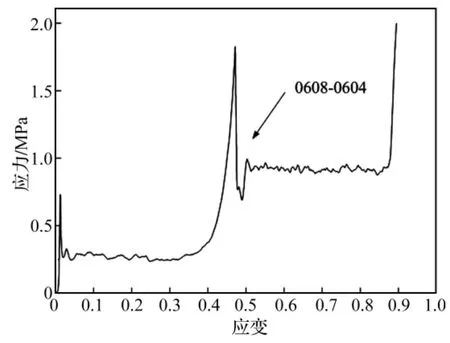
图10 不同规格铝蜂窝串联压缩试验应力-应变曲线图Fig.10 Experimental stress-strain curve of series honeycomb structures with different specifications

对相同规格铝蜂窝缓冲结构串联压缩试验，虽采用规格相同试件，但因加工的差异及试件孔格一致性不同，使两试件不可能完全一致。因此试验过程中两试件并未同时发生大规模变形，而与不同规格试验类似:强度较弱的铝蜂窝试件先变形进入屈服阶段，当该试件进入密实化阶段时其受到载荷会急剧攀升，当达到强度较大的蜂窝试件峰值载荷时第二个试件进入屈服阶段。相同规格铝蜂窝缓冲结构串联压缩试件应力-应变曲线见图11。该图表明，相同规格铝蜂窝试件串联压缩试验，每级试件的平均应力基本相同，试件的峰值应力相差不多，因每个试件的随机性较大，两试件不可能完全一致，因此会产生微小差异。

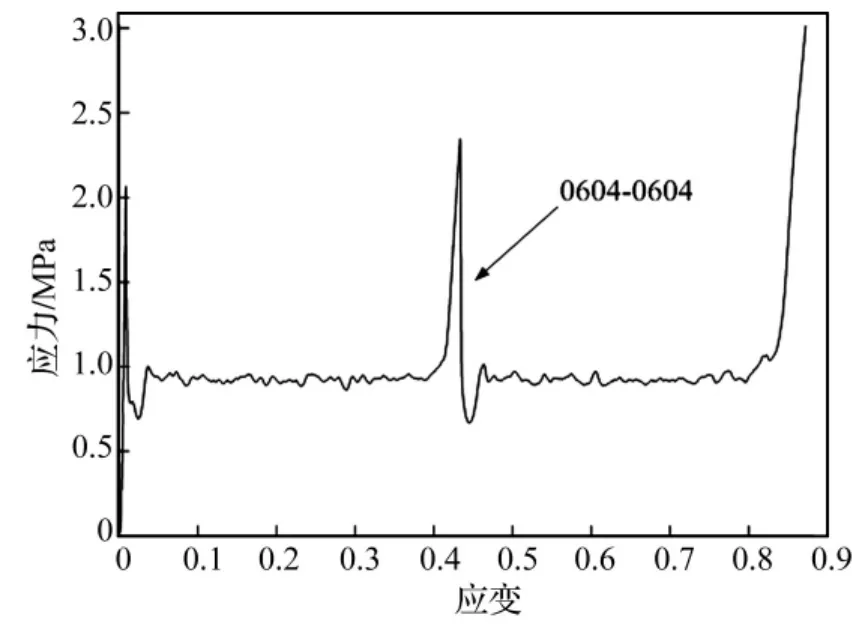
图11 相同规格铝蜂窝串联压缩试验应力-应变曲线图Fig.11 Experimental stress-strain curve of series honeycomb structures with same specifications

5 仿真与试验结果分析

平均应力及极限应变是衡量铝蜂窝缓冲器吸收能量的重要指标。设计缓冲器时，利用该两指标可推算出吸收能量的大小，同时由极限应变可获得蜂窝缓冲器的可压缩行程。对铝蜂窝材料的平均应力已有大量研究，其中Gibson等［14］通过对铝蜂窝材料进行大量的理论与试验研究后给出铝蜂窝材料受异面压缩时平均应力半经验公式。对正六边形胞元双层铝蜂窝材料，该公式为:

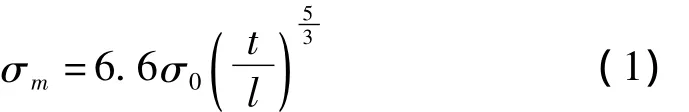
式中:t为蜂窝胞元厚度;l为壁厚t胞元边长;σ0为蜂窝基体屈服极限;σm为蜂窝材料平均应力。

式(1)在t/l值较大时准确性较低。本文基于蜂窝材料的对称性特点，以Y型蜂窝胞元为研究对象，采用Tresca屈服准则推导出蜂窝材料在静态压缩下的平均应力本构方程，通过一系列试验，验证了该本构方程的正确性［16-17］。与经典半经验公式相比，该公式精度更高。因此采用该公式对串联式铝蜂窝缓冲结构各级平均应力进行研究。基于Tresca屈服准则的蜂窝材料异面静态压缩平均应力公式［16-17］为:

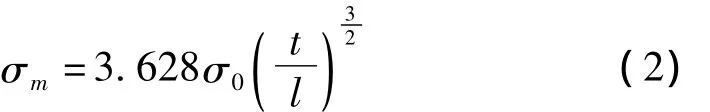
表2 铝蜂窝串联压缩各级蜂窝平均应力值Tab.2 Plate stress of series aluminum honeycomb structures under compression

铝蜂窝串联压缩单级蜂窝平均应力仿真值、试验值和基于Tresca屈服准则的理论值见表2。仿真值与理论值相差无几，但仿真与理论所得铝蜂窝平均应力值略高于试验值。

六种规格的串联式铝蜂窝缓冲器受异面静态压缩载荷作用下的应力-应变曲线见图12。对相同规格铝蜂窝串联压缩的仿真模型为标准正六边形蜂窝胞元，上下两级蜂窝强度相同。在压缩仿真过程中两级蜂窝同时变形进入屈服阶段，而实际试验中因试件的随机性使两级蜂窝强度不会完全相同，压缩过程中会出现与不同规格铝蜂窝串联压缩试验类似情况，即强度不同，变形过程出现两个阶段，并在整个压缩过程中存在两个峰值应力。而同种规格仿真不能模拟试验的随机差异，故只存在一个峰值应力。

表3 铝蜂窝串联压缩极限应变值Tab.3 Limiting strain values of series aluminum honeycomb structures under compression

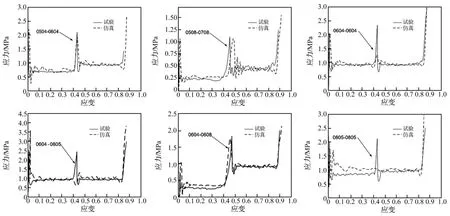
图12 串联铝蜂窝压缩试验与仿真应力-应变曲线对比图Fig.12 Experimental and numerical stress-strain curves of the specimens under quasi-static compression

对单个铝蜂窝缓冲器静态压缩仿真与试验研究发现，单个铝蜂窝缓冲器的极限应变稳定在 0.8左右［16-17，19-20］。 本 文的仿真与试验研究表明，串联铝蜂窝静态压缩的极限应变稳定在0.85左右。文献［20］中，通过仿真分析验证了二级串联蜂窝结构压缩仿真其各级平均应力与单个蜂窝结构受压缩仿真的平均应力值几乎相同。因此对同一尺寸蜂窝，与单个铝蜂窝缓冲器相比，该串联式组合铝蜂窝缓冲器能吸收更多能量。串联蜂窝结构受压缩载荷极限应变的仿真值与试验值见表3。由表3看出，仿真值与试验值偏差在2%内，仿真结果有足够精度，能准确计算出串联式蜂窝结构的可压缩行程。为精确设计串联式蜂窝结构缓冲器提供了依据。

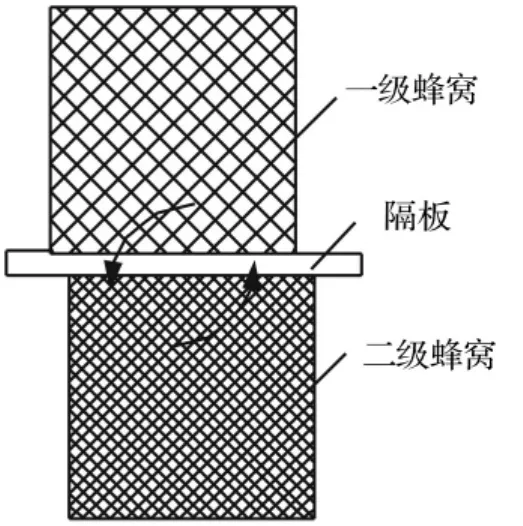
图13 串联铝蜂窝压缩试验对中偏差示意图Fig.13 Sketch of aligned bias series honeycombs under crash test

分析表3发现，平均应力试验值略低于仿真值，由图9，仿真与试验应力-应变曲线在弹性阶段吻合较差。发生该现象的主要原因为，试验时因中间加有隔板，上下两级蜂窝缓冲器对中困难，两者中心未重合，如图13所示。压缩试验时上下两级蜂窝错位，使整个串联系统受力矩作用，因此蜂窝在受到异面压缩载荷时不但发生异面变形，在面内同时发生变形，使异面方向的平均应力与峰值应力减弱，故试验值略低于仿真值。同时仿真未能模拟加工蜂窝粘接所用粘胶，试验中蜂窝受压缩力作用可能产生粘胶破裂情况，而粘胶的力学特性与铝箔相差较大，也会造成仿真结果与试验结果有偏差。

6 结论

基于Patran/DYNA有限元软件，结合试验，对串联式铝蜂窝缓冲结构受异面压缩载荷作用的动态响应进行研究，结论如下:

(1)建立的串联铝蜂窝缓冲结构受异面压缩载荷作用的有限元模型可准确模拟铝蜂窝材料在受异面压缩载荷时的材料的叠缩坍塌;通过与试验数据对比，证明该仿真模型可较好模拟整个铝蜂窝受异面压缩载荷作用时的变形过程，能准确提供整个变形过程铝蜂窝所受载荷信息。

(2)通过与试验结果对比，证明该仿真模型可准确模拟串联铝蜂窝缓冲结构受异面压缩载荷下的平均应力和极限应变，准确反应缓冲器的吸能能力和可压缩行程，使理论上设计缓冲器成为可能。通过仿真与试验分析，证明对同一尺寸蜂窝，串联铝蜂窝缓冲器与单级铝蜂窝缓冲器相比，其极限应变稳定在0.85左右，能吸收更多能量。

(3)本文所提有限元仿真模型成本低，不受试验条件限制，且准确性较高，为一种有效的研究方法。

［1］Yamashita M，Gotoh M.Impact behavior of honeycomb structures with various cell specifications-numerical simulation and experiment［J］. InternationalJournalofImpact Engineering，2005，32(1-4):618-630.

［2］ Hong S T，Pan J，Tyan T.Quasi-static crush behavior of aluminum honeycomb specimens under compression dominant combined loads［J］.International Journal of Plasticity，2006，22(6):1062-1088.

［3］Zhou Q Q，Mayer R R.Characterization of aluminum honeycomb material failure in large deformation compression，shear，and tearing［J］.Journal of Engineering Materials and Technology，2002，124(4):412-420.

［4］Doengi F，Burnage S T，Cottard H.Lander shock-alleviation techniques［R］.ESA Bulletin 93，1998.

［5］王 闯.四腿桁架式月球着陆装置设计及其着陆缓冲技术研究［D］.哈尔滨:哈尔滨工业大学，2008.

［6］ Wierzbicki T.Crushing analysis of metal honeycombs［J］.Int.J Impact Engng，1983，1(2):157-174.

［7］ Yasui Y.Dynamic axial crushing of multi-layer honeycomb panels and impacttensile behaviourofthe component members［J］.International Journal of Impact Engineering，2000，24(6-7):659-671.

［8］McFarland R K.Hexagonal cell structures under postbuckling axial load［J］.AIAA Journal，1963，1(6):1380-1385.

［9］Aktay L，Johnson A F，Kroplin B H.Numerical modeling of honeycomb core crush behaviour［J］.Engineering Fracture Mechanics，2008，75(9):2616-2630.

［10］ Wu E B，Jiang W S.Axial crush of metallic honeycombs［J］.International Journal of Impact Engineering，1997，19(5-6):439-456.

［11］ Liaghat G H，Alavinia A.A comment on the axial crush of metallic honeycombs by Wu and Jiang［J］.International Journal of Impact Engineering，2003，28(10):1143-1146.

［12］Liu Y，Zhang X C.The influence of cell micro-topology on the in-plane dynamic crushing of honeycombs［J］.International Journal of Impact Engineering，2009，36(1):98-109.

［13］Zhang X，Cheng G D，Zhang H.Theoretical prediction and numerical simulation of multi-cell square thin-walled structures［J］.Thin-Walled Structures，2006，44(11):1185-1191.

［14］ Gibson L J，Ashby M F.Cellular solid:structure and properties，2nd ed［M］.Cambridge University Press，1997.

［15］ Hallquist J.LS-DYNA user's manual［A］.Version:LSDYNA 970ed. Livermore Software Technology Corporation，2003.

［16］罗昌杰，周安亮，刘荣强，等.金属蜂窝异面压缩下平均压缩应力的理论模型［J］.机械工程学报，2010，18:52-59.

LUO Chang-jie，ZHOU An-liang，LIU Rong-qiang，et al.Average compressive stress constitutive equation of honeycomb metal under out-of-plane compression［J］.Chinese Journal of Mechanical Engineering，2010，46(18):52-59.

［17］罗昌杰.腿式着陆缓冲器的理论模型及优化设计研究［D］.哈尔滨:哈尔滨工业大学，2009.

［18］ Li M，Deng Z Q，Liu R Q，et al.Crashworthiness design optimisation of metal honeycomb energy absorber used in lunar lander［J］.International Journal of Crashworthiness，2011，16(4):411-419.

［19］Li M，Liu R，Guo H.A study on out-of-plane compressive properties of metal honeycombs by numerical simulation［J］.High Performance Structures and Materials Engineering，2011，217-218:723-727.

［20］李 萌.腿式着陆器用泡沫铝和铝蜂窝缓冲器仿真与试验研究［D］.哈尔滨:哈尔滨工业大学，2009.