轴／径向耦合式非接触型压电作动器的研究

陈 超 李 繁 贾 兵 王均山

南京航空航天大学机械结构力学及控制国家重点实验室，南京，210016

0 引言

1996年，日本的Hashimoto等［1］提出可利用近声场悬浮现象构造高刚度的悬浮系统或轴承的观点。该悬浮系统或轴承具有结构简单紧凑，无需专门的反射源，对悬浮物体没有特殊要求的优点，开启了对基于近场声悬浮的非接触式压电作动器和超声电机研究的时代。声辐射压力和体声流通常被认为是非接触式超声电机的驱动力来源［2］，同时它也为非接触式操作和传输提供了一种新的作用方式。特别地，在大多数机械支撑的驱动和传动系统中，如高速电机、球轴承等的使用寿命主要取决于支承部分的性能，采用非接触式的支承方式可有效减少摩擦和阻尼干扰力矩［3－4］，改善整个传动系统的特性和延长使用寿命。因此，非接触式压电作动器在航空航天领域、非接触式轴承传动、姿态敏感器等中具有广阔的应用前景［5－10］。

本文提出了一种轴／径向耦合式压电作动器，该作动器可分别沿轴向和径向对球转子施加超声近场作用，在深入分析其工作机理的基础上，探讨了轴／径向悬浮装置在不同的耦合情况下对球转子运行状态的控制方式。其次，基于有限元法对轴向压电悬浮装置产生的声场进行了仿真分析，得到了结构的振型分布与声场分布的关系。最后，搭建了样机的特性测试系统，对轴向压电作动器样机开展了悬浮稳定性试验研究。

1 轴／径向耦合式压电作动器的机理

图1为轴／径向耦合式压电作动器装配图。当对轴向压电陶瓷片或径向压电陶瓷片施加激励电压时，依靠压电陶瓷的逆压电效应，可以在轴向定子或径向定子上激发所需要的振动，使得轴／径向耦合驱动装置由分解的轴向和径向压电作动器耦合而成，从而在定子的球形表面和球转子之间形成声场，通过声辐射压力悬浮、声黏性力驱动球转子悬浮和旋转。

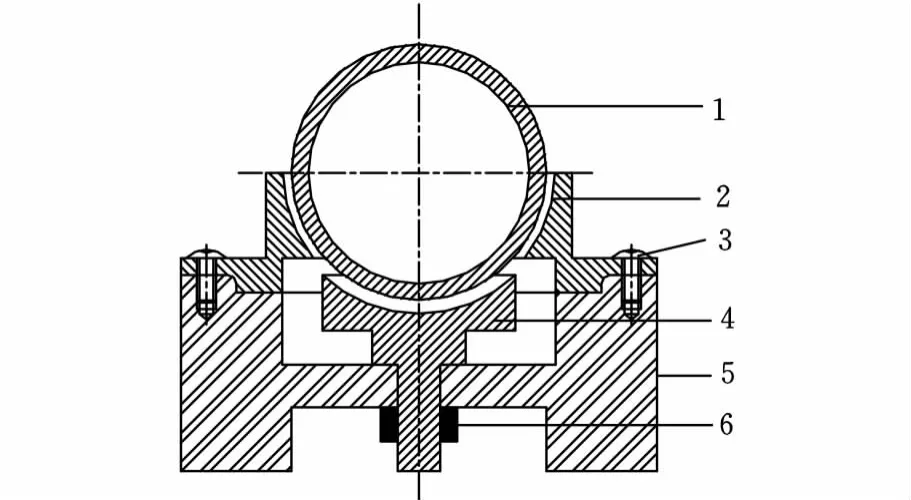
图1 轴／径向耦合式压电作动器装配图

轴／径向耦合式超声悬浮陀螺通过轴向或径向两个声场辐射模块调控，图2为轴／径向耦合式压电作动器样机，其中，通过施加不同组合的激励电压，轴向悬浮装置或径向悬浮装置的振动可分别为行波或驻波状态，不同的耦合构成情况如表1所示。

图2 轴／径向耦合式压电作动器样机

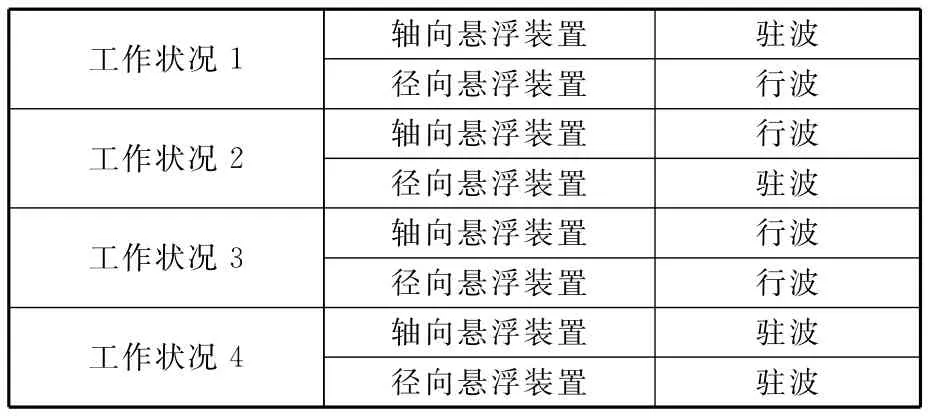
表1 悬浮装置振动的不同耦合状态

其中，若轴向悬浮装置被激励产生驻波振动则诱发的声场主要对球转子施加悬浮效果，若被激励产生行波，则诱发的声场对球转子同时有悬浮和驱动其旋转的效果；同样地，若径向悬浮装置被激励产生驻波振动则主要对球转子施加悬浮效果，若被激励产生行波，则对球转子同时有悬浮和驱动其旋转的效果。因此，工作状况1、2和3的组合均可悬浮和驱动球转子旋转，而且由于轴向悬浮装置和径向悬浮装置的不同组合使得被诱发出的声场中的悬浮和旋转驱动力的耦合强度不同，球转子可获得不同的悬浮和旋转效果。

特别地，当轴向和径向声场辐射模块工作在4组合状态时，仅对球转子提供沿径向的作用力，球转子可获得更高的悬浮刚度；而当轴向和径向声场辐射模块工作在3组合状态时，可同时提供沿径向的悬浮力和沿圆周切向的驱动力，此时球转子在获得高刚度悬浮的同时，也可实现大角动量的高速旋转。

因此，通过定子中轴／径向悬浮装置的不同振动形式组合，可改变定子和球转子之间声场的悬浮和旋转驱动力耦合强度，进而有效地改变球转子获得的悬浮驱动力，达到调节球转子运行状态的目的。

2 轴向悬浮装置声场仿真

COMSOL Multiphysics 4.2是一个用于模拟基于偏微分方程（PEDs）的科学和工程应用的人机交互式平台，本文利用它对碗式定子进行声场仿真。

首先通过COMSOL特征频域计算，得到轴向悬浮装置的固有频率为99.4855kHz，其次进行频域分析，通过压电设备模块和声压模块来仿真陀螺定子在工作模态下的声场分布。其有限元模型和边界条件的设置如图3所示，网格数为147 720。在实际中，悬浮装置振动产生的声场将向空间辐射出去，但若将空气域的体积设置得很大，会增加所需要的网格数和计算时间。因此，通过在模型中设置特定的边界来模拟声场向无限远处辐射的效果，可将模型中空气的分析域限制在一个合适的范围。在图3所示模型中，利用柱面波辐射、完美匹配层以及平面波辐射边界条件来拟合声场向四周传递（而非反射）。即在轴向悬浮装置的上下平面（轴线方向）设置平面波辐射，目的是为了尽可能地模拟真实环境，即模拟真实情况下的无限远空间，且不带来计算时间上的增加。

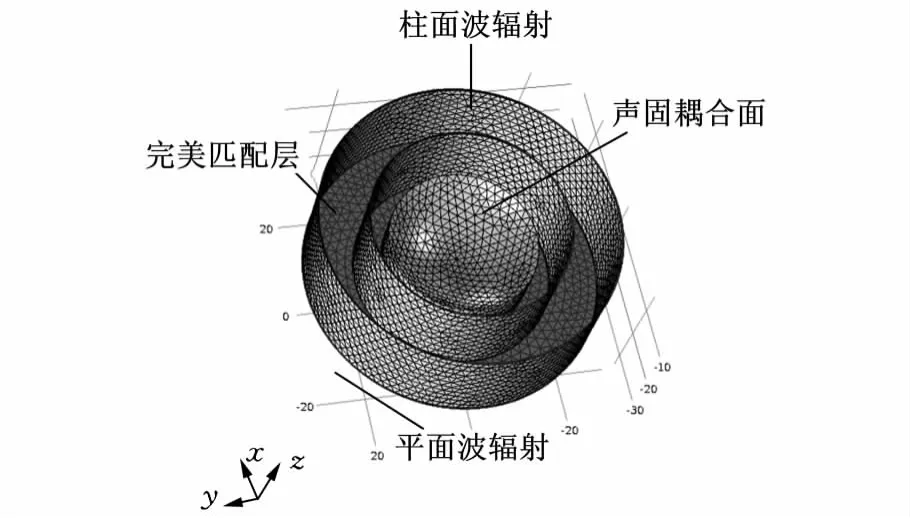
图3 轴向悬浮装置声场仿真模型

经计算得到其位移分布如图4所示，在输入电压峰－峰值为100V时，最大变形为9.0045μm，其振型为B（0，5）。

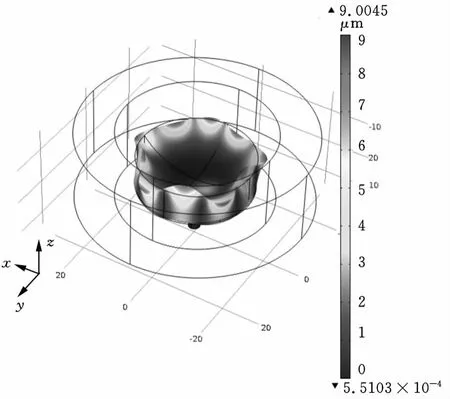
图4 轴向悬浮装置位移分布

通过后处理可得到声压分布，其结果如图5所示。从图中可以看出，在驱动电压峰－峰值为100V的作用下，轴向悬浮装置最大声辐射压为812.88Pa，此时声辐射压流向为逆时针方向，表明此时形成行波。

轴／径向耦合式定子，是通过轴向悬浮装置和径向悬浮装置共同组合来驱动球转子的，所以研究的对象主要是驱动面处的位移分布和声压分布。图6为轴向悬浮装置驱动面处的声压分布，振型分布与声压分布是有一定对应关系的，即有多少个峰值位移，就有多少个峰值声压。

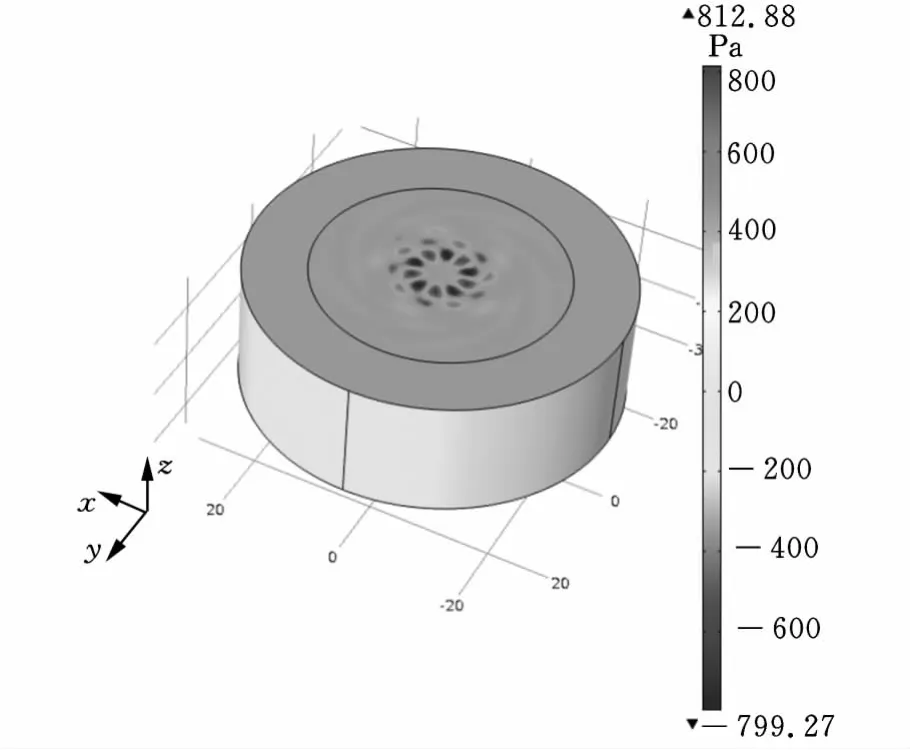
图5 轴向悬浮装置声压分布

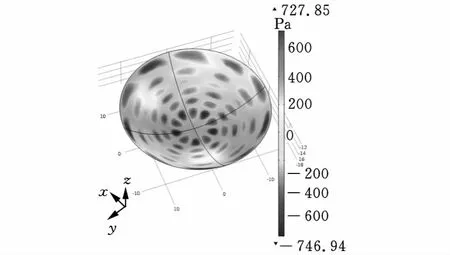
图6 轴向悬浮装置驱动面处声压分布

从图7的截面图可以看出，声波是一种疏密波，即声压是正负交替向前传播，随着距离的增加声压会慢慢衰减，最终与外界大气压一致。轴向悬浮装置的声压分布是指向中心线的，即具有一定的指向性，一部分力用来克服转子重力，另一部分用来平衡水平方向的扰动力。

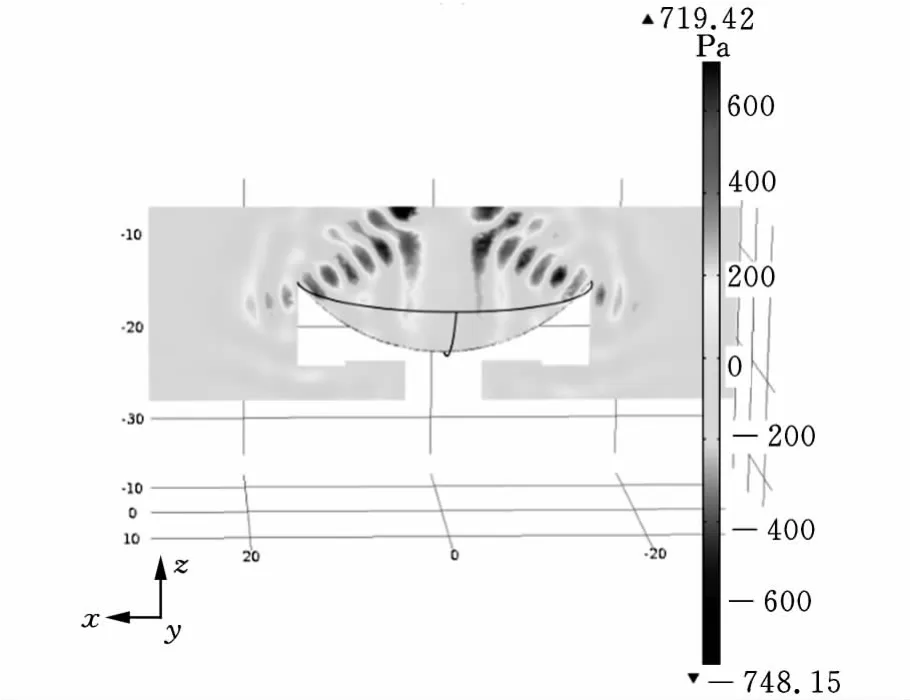
图7 轴向压电作动器截面声压分布

3 轴向压电作动器悬浮稳定性及转速特性研究

球转子是通过一定频率的空间声场来支承和驱动的，所以有必要研究稳定状态时，其悬浮高度是否也存在相应的变化和抖动。下面将针对半实心钢球转子和铝球转子来进行研究，驱动电压是峰－峰值为300V的电压，激励电压频率为94.73kHz，其中钢转子质量为111.2g，铝转子质量为39.9g，试验装置如图8所示。

图8 轴向压电作动器稳定性试验

轴向悬浮装置稳定性试验通过非接触式激光位移传感器来测量，首先对钢球转子进行了稳定性试验，测试结果如图9所示。将其中的数据进行平均处理，得到钢球转子竖直抖动最大幅值为20.308μm，悬浮高度为30.532μm。而实心半铝球转子抖动最大振幅为24.678μm，悬浮高度为45.145μm如图10所示。

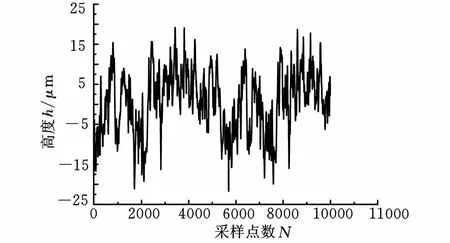
图9 实心半钢球转子稳定性试验

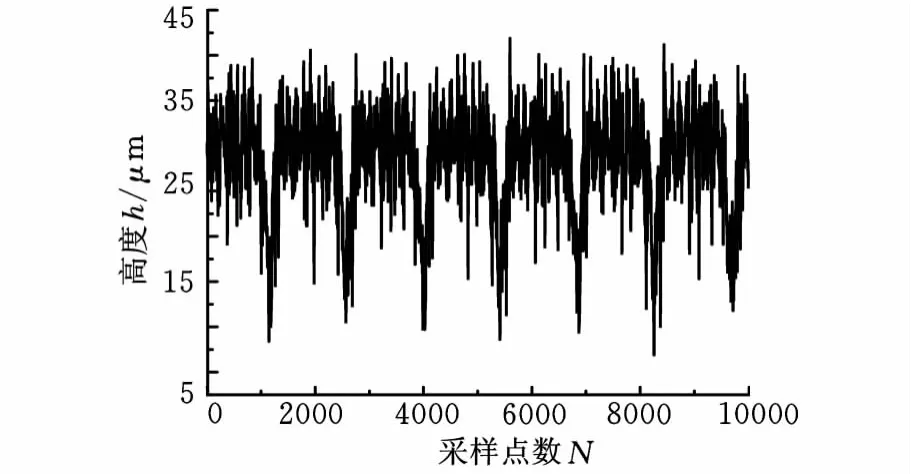
图10 实心半铝球转子稳定性试验

球转子外径为38mm，材料为硬铝，使用胜利仪器非接触式激光转速表DM6234P＋进行半球形转子的转速测试，作动器驱动电压峰－峰值为400V，驱动频率为94.73kHz，测得转速为691.5r／min，转子质量为21.350g，如图11所示。

4 结语

图11 轴向悬浮装置测速装置

对轴／径向耦合式压电作动器进行了工作机理分析，并加工制造出了样机。通过声场的计算分析明确了振型分布与声压分布的一一对应关系。对轴向压电作动器样机进行了悬浮稳定性试验，当激励电压峰—峰值为300V时，得到了当铝球转子质量为39.9g时，最大抖动幅值为24.678μm；当钢转子质量为111.2g时，最大抖动幅值为20.308μm。通过比较钢球转子与铝球转子的抖动性大小可初步得知，在一定范围内，较大的质量有利于球转子的稳定，其动力学机理有待更深入地研究和分析。

［1］Hashimoto Y，Koike Y，Ueha S.Near－field Acoustic Levitation of Planar Specimens Using Flexural Vibration［J］.J.Acoust.Soc.Am.，1996，100（4）：2057－2061.

［2］Hu J H，Nakamura K.Characteristics of a Noncontact Ultrasonic Motor Using Acoustic Levitation［C］／／IEEE Ultrasonic Symposium.San Antonio，1996：373－376.

［3］Ide T，Friend J，Nakamura K，et al.A Non－contact Linear Bearing and Actuator via Ultrasonic Levitation［J］.Sensors and Actuators A，2007，135：740－747.

［4］Isobe H，Kyusojin A.Frequency Characteristics of Noncontact Ultrasonic Motor with Motion Error Correction［J］.Precision Engineering，2007，31：351－357.

［5］Ueha S，Hashimoto Y，Koike Y.Non－contact Transportation Using Near Field Acoustic Levitation［J］.Ultrasonics，2000，38：26－32.

［6］彭太江，杨志刚，阚君武，等.超声波悬浮能力及其试验研究［J］.压电与声光，2006，28（2）：229－235.Peng Taijing，Yang Zhigang，Kan Junwu，et al.Experimental Research on Ultrasonic Levitation Ability［J］.Piezoelectrics ＆ Acoustooptics，2000，38：26－32.

［7］季叶，赵淳生.一种圆筒型非接触式超声电机［J］.南京航空航天大学学报，2005，37（6）：690－693.Ji Ye，Zhao Chunsheng.Cylinder Type Non－contact Ultrasonic Motor［J］.Journal of Nanjing University of Aeronautics and Astronautics，2005，37（6）：690－693.

［8］唐方圆.凹柱面支撑超声波悬浮轴承设计与实验研究［D］.长春：吉林大学，2006.

［9］常颖，吴博达，杨志刚，等.超声波悬浮推力轴承承载能力及减摩性能［J］.吉林大学学报（工学版），2004，34（2）：222－225.Chang Ying，Wu Boda，Yang Zhigang，et al.Bearing Capacity and Anti－friction Behavior of Ultrasonic Vibration Bearing［J］.Journal of Jilin University（Engineering and Technology Edition），2004.34（2）：222－225.

［10］朱金冬.超声波支承陀螺仪的研究［D］.西安：西北工业大学，2007.