贵广铁路大跨预应力混凝土连续梁端部局部应力分析

陈 艳

(中铁第四勘察设计院集团有限公司，武汉 430063)

1 桥梁概况

1.1 桥型简介

贵广铁路大跨预应力混凝土连续梁，跨径组合为(64+108+64)m，列车设计时速250 km。桥梁结构采用变截面三跨连续箱梁，中支点处梁高7.5 m，端部及跨中梁高4.5 m，其底缘按照半径为443.5 m的圆曲线过渡变化。顶板厚37 cm;腹板厚从40 cm变化到110 cm，根部局部加厚至160 cm;底板厚从46 cm变化至97.1 cm，根部局部加厚至150 cm。箱梁采用挂篮悬臂浇筑法施工，每个悬臂阶段张拉锚固纵向、竖向和横向预应力束。

对于后张法混凝土构件，张拉时预应力是通过锚具将力传递给混凝土，因此锚下混凝土将承受较大的局部压应力，端部混凝土在局部较大压应力作用下将会出现裂缝甚至破坏，影响主梁的长期工作性能。锚具附近裂缝产生的原因主要为两种应力作用的结果:一种是由于预应力的局部作用，沿着预应力作用线的方向上产生的横向拉应力，称之为劈裂应力;另一种是远离预应力作用点的断面，称为剥落应力。大跨度预应力混凝土连续梁端部锚固预应力钢束多，并受构造尺寸限制，梁端锚具布置间距密，锚固作用互相影响，因此研究多个锚具相互作用下的梁端局部承压性能，防止梁端锚固区混凝土破坏，并以此指导设计是非常必要的。

1.2 梁端部构造

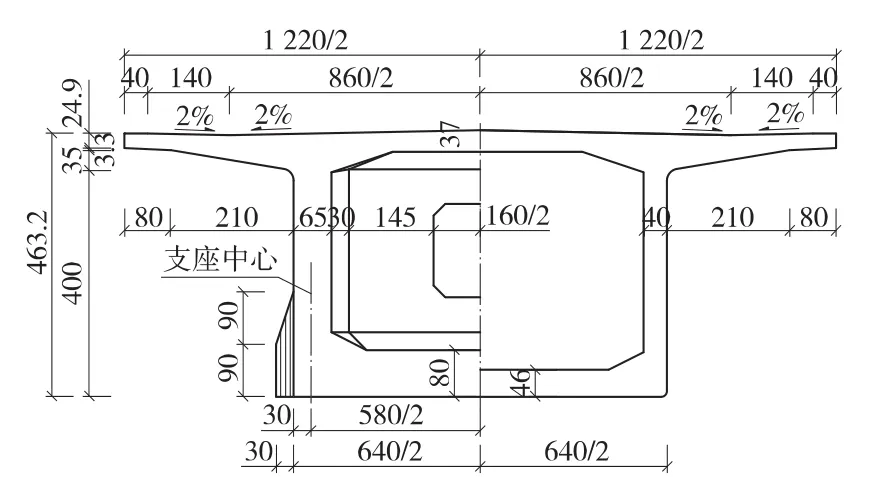
图1 端部截面尺寸(单位:cm)

该桥预应力混凝土连续梁端部截面在梁端支座处设置横隔板，横隔板厚度为145 cm。主梁混凝土采用C55，支座采用球型支座。为了防止梁端在局部压应力作用下梁端混凝土压裂，在梁端一定范围内布置了加强钢筋。端部截面和三向钢束布置分别如图1、图2所示。钢束规格和型号如表1所示。

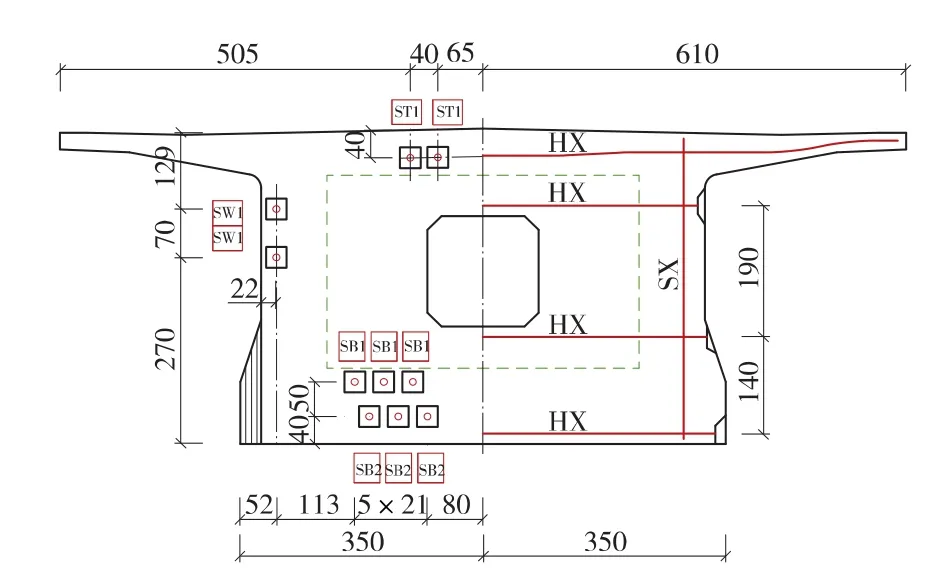
图2 端部三向钢束布置(单位:cm)

表1 钢束规格及应力

2 有限元模型的建立

梁端部局部应力分析采用有限元软件ANSYS建模，由于本文主要研究边跨梁端部锚固区局部应力场，所以选取梁端部约4 m长的节段长度进行模拟，其中混凝土采用实体单元Solid95模拟，预应力钢筋采用杆系单元Link8模拟。在ANSYS建模中，预应力混凝土分析实体力筋法的常规处理过程有2种方法，一是体分割法，二是采用独立建模耦合法。

(1)体分割法

该法的基本思想是先建立实体，再用工作平面和预应力筋拖拉形成的面，将实体分割，分割面与实体相交位置即为预应力力筋线。通过每段预应力力筋线所在平、立面与实体分割，预应力筋在实体中的位置即能建立，并与相应的实体共线。这种方法建模，预应力筋位置准确，计算结果精确，但当预应力筋线形复杂且数量很多时，建模难度很大。

(2)独立建模耦合法

该法的基本思想是将实体和预应力筋独立建立几何模型，分别划分单元，然后采用耦合方程将预应力筋单元和与之距离最近的实体单元联系起来。这种方法建模特别简单，缺点是当实体单元划分不够密时，预应力筋节点位置与实际位置有差别，特别是当预应力筋间距较密、结构复杂时，耦合方程中的单个从节点(实体)有可能与多个主节点(预应力筋)耦合，导致耦合错误，修正起来非常麻烦。

本文研究的预应力混凝土连续梁梁端模型为三向预应力结构，箱梁构造复杂，预应力筋种类多、线形空间变化，显然采用上文2种常规建模方式，很难对梁端部进行精确的模拟分析。因此，为了真实反映结构细部受力机理，根据结构特点，采用上述2种方法相结合的方式进行建模。建模主要过程如下。

①建立箱梁实体和纵向预应力力筋线的独立几何模型。

②在梁端部以每根纵向预应力力筋线端部为中心建立相应的锚具和管道平面，同时将各个锚具和管道平面以力筋线端点为中心划分为对应的4个部分，分别沿每根力筋线为路径将锚具和管道平面通过拖拉生成以力筋线为中心线的空间实体，其中锚具的大小和长度根据实际尺寸确定。

③将纵向预应力力筋线所在的空间圆柱体与箱梁实体进行互分，分隔成多个边界相互关联的实体，如图3所示。

④在互分后的模型中找出纵向预应力力筋线并进行归类。

⑤建立横向和竖向预应力筋，按上述独立建模耦合法将横向和竖向预应力筋单元与实体单元耦合，预应力的加载按降温法模拟，最后施加边界条件和求解。

本文采用的建模方法优点在于利用箱梁体与预应力筋所在实体的互分，得到边界相互关联的几何模型，预应力筋模拟精确，并且端部锚具也能按实际情况模拟，大大降低了建模难度和节约了建模时间。有限元模型如图4所示。

图3 预应力筋与箱梁互分示意

图4 有限元模型

3 计算结果

本文分析计算时不考虑结构的材料非线性、几何非线性和混凝土的收缩徐变效应，并假定结构受力时为小变形。计算中考虑的边界条件是根据结构的实际受力状态，按照结构静定的基本原则对局部模型梁端部支座位置范围内的节点施加竖向和横向约束，对远预应力锚固端的梁截面节点施加固定约束，计算荷载仅考虑预应力和结构自重。梁端局部模型的分析结果以应力云图的形式给出，限于篇幅，本文仅示出部分结果。图5和图6分别为沿腹板钢束中心线纵向剖面和沿顶、底板钢束中心线纵剖面混凝土的主应力计算结果，图7为距离张拉锚固端0～2.5 m不同位置处横截面的混凝土主压应力计算结果。

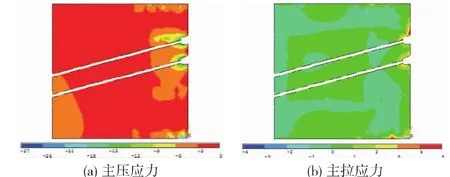
图5 腹板钢束处纵剖面应力云图(单位:MPa)

(1)从图5和图6可以看出，沿钢束中心线方向的混凝土主应力分布具有相似特征。腹板处最大主压应力约为27 MPa，顶底板处最大主压应力约为18 MPa;主要分布在距张拉端0.3 m范围(锚具长度)内，而且应力梯度下降很快，在距张拉端0.5 m处，最大主压应力分别下降至约15 MPa和12 MPa;在距张拉端2.5 m处，各部分的最大主压应力分布基本均匀。

图6 顶、底板钢束处纵剖面应力云图(单位:MPa)

图7 横截面主压应力云图(单位:MPa)

(2)从图5和图6还可以看出，在腹板钢束和顶、底板钢束锚固位置处，混凝土的最大主拉应力主要发生在张拉端锚垫板孔道周围，局部应力集中处最大拉应力约为5 MPa，在锚锭板以外的锚具喇叭口区域内最大拉应力约为3 MPa。除此之外由图6(b)可以看出，顶、底板钢束之间的区域，混凝土最大拉应力亦处于较高水平，为2～3 MPa，纵向分布深度约为50 cm。锚垫板周围产生较大的拉应力是由于锚锭板传递压力引起的，因锚垫板尺寸较小，在预应力作用下产生压缩变形后必然在周围产生一定的拉应力。

(3)从图7的横断面混凝土主压应力云图可以看出，最大主压应力沿着钢束方向迅速下降，并逐渐趋于均匀，这与图5和图6所反映的情况一致。另外从图7亦可以得知，在锚垫板位置处，锚具2倍孔径范围内的混凝土主压应力水平较高并呈独立的环形分布，远离锚垫板后每个锚垫板下的最大主压应力区域逐渐扩散，在距离锚垫板0.3 m处已相互连接大致呈矩形分布，其后已非常均匀。

4 结论

通过对此预应力混凝土连续梁端部预应力锚固区的局部进行有限元计算可以得出以下结论。

(1)锚垫板2倍孔径范围内以下混凝土的主压应力水平较高，最大约为27 MPa，随着深度的增加，应力急剧减小，在距端部2倍锚具长度后应力水平已趋于均匀，这说明预应力的作用已扩散至混凝土中。根据铁路规范，C55混凝土轴心抗压极限强度为37 MPa，因此锚固区混凝土最大主压应力未超出材料的极限强度。考虑到实际施工偏差，对此区域设置一定的锚下钢筋网以分散应力是合理和必要的。

(2)在锚垫板四周位置，混凝土出现较大的主拉应力，最大值约为5 MPa，远超出C55级混凝土的轴心抗拉极限强度3.3 MPa，但分布区域很小，属应力集中现象。在此区域以外，锚具喇叭口和顶、底板钢束之间区域内混凝土最大主拉应力水平亦较高，最大主拉应力已在3 MPa以下，接近于材料的极限强度，因此设计时需要对该区域特别是顶、底板之间的横梁封锚端表面采取钢筋加强措施，防止预应力张拉时混凝土表面出现开裂。

(3)因锚下混凝土的最大主压应力仅在锚具2倍孔径范围内和锚具深度范围内水平较高，即混凝土纵、横向距离锚垫板越近压应力越大，远离锚垫板后压应力区域逐渐扩散并趋于均匀，因此锚具间距对于锚下混凝土应力的分布影响不大，当钢束之间有一定的距离时锚下应力的计算可由单锚分析确定。

［1］彭正中，赵曼，王新敏.预应力混凝土箱梁的端块应力分析［J］.铁道标准设计，2007(5):50-52.

［2］张玉文.大跨度双线无砟轨道预应力简支箱梁端锚固区应力分析［J］.铁道标准设计，2010(4):29-32.

［3］肖飞.大跨度预应力混凝土简支箱梁的梁端应力分析［J］.铁道标准设计，2004(8):78-80.

［4］赵磊，邵铭，哈大客运专线56 m简支箱梁预应力钢束布置及梁端应力分析［J］.铁道标准设计，2012(2):70-73.

［5］罗继前，肖礼经，王卫锋，颜全胜，谭毅平.预应力混凝土连续梁桥锚下局部应力分析［J］.中外公路，2003，23(6):48-50.

［6］陈嘉毅，谢旭，徐爱敏，赵剑发.大跨度预应力混凝土箱梁锚固区局部应力研究［J］.浙江大学学报，2009，43(6):1077-1082.

［7］许惟国，何广汉.连续刚构桥锚固区局部应力的研究［J］.西南交通大学学报，2004(3):371-374.

［8］何旭辉，黎徽.锚固区布置对预应力T梁梁端局部应力影响研究［J］.城市道桥与防洪，2009(6):171-174.

［9］丁伟亮，李德建，魏俊，刘朝晖.预应力束张拉顺序对锚下局部应力影响分析［J］.交通科技与经济，2008(5):10-12.

［10］白鸿国，袁常青.秦沈线32 m双线整孔箱梁端部应力分析［J］.铁道勘察，2005(3):94-95.