基于道路通行概率的战时油料前送最优路径研究

王 强，李 横，崔子庆，高 诤WANG Qiang,LI Heng,CUI Zi-qing,GAO Zheng

（1.后勤工程学院，重庆 401311；2.汕头警备区，广东 汕头 515038）

(1.Logistical Engineering University,Chongqing 401311,China;2.Shantou Garrison,Shantou 515038,China)

本质上，油料前送最优路径的求解就是在后方油库与战役野战油库两点之间寻找一条军事效益最好的路径。无论是路径的“最优”有哪个因素——距离最短、时间最短、费用最少或者安全性最高，其核心算法都是最短路径算法。在战时，要保证油料保障的安全、准确和及时，就要求找出一条 “最优”路径。战时油料前送，要求安全顺利并且时间最短，所以交通网络抽象图的边权是运油车在该段道路上行驶所需的时间。模型结合战时的道路损毁情况，采用图论经典的D算法对最优路径进行求解。

利用图论的经典理论和GIS存储的相关数据信息研究目标区域内的道路战时通行情况，并由此得出运油车前送油料的最优路径。首先计算出战时道路通行概率P，用此概率乘以运油车平时在该路段的行驶速度Si1，得出战时运油车在该路段的行驶速度Si2，用该路段长度Li除以Si2，得出运油车在该路段所需要的时间Ti。将Ti作为道路抽象网络图的路边的权，得出战时运油车在目标道路上行驶的时间矩阵，以选择从后方油库到战役野战油库所需最短时间的路线为目标，建立最短路径问题的数学模型，利用经典的D算法确定最短路径。将此方法应用于某运油分队执行油料前送任务，寻找出符合要求的最优路径。

1 模型使用技术和算法

1.1 缓冲区 （Buffer）分析

地理信息空间关系分析主要包括缓冲区分析、叠加分析、空间集合分析和专业分析等。本文所才采用缓冲区分析是油料保障地理信息系统的基本空间操作功能之一。缓冲区分析是围绕空间的点、线、面实体，自动建立其周围一定宽度范围内的多边形，用以识别这些实体或主体对邻近对象的辐射范围，以便为某项分析或决策提供依据。其基本思想就是给定一个空间实体或集合，确定它们的邻域，邻域的大小由设定的邻域半径R来确定。要分析前送油料的最优路径，则需对前送油料目标道路建立线缓冲区进行分析。线要素的缓冲区是以线为轴，以R为距离作两侧的平行线，在机动路线的两端以R为半径作半圆，平行线和半圆所围区域就是缓冲区。如图1所示。

1.2 Dijkstra算法

Dijkstra算法 （简称D算法）是寻求从一固定起点到其余各点的最短路径的最有效算法之一，是一种图上标记作业法，每次在计算完成一个探索节点就产生一个标记，直至所有路网节点被标记。算法思想是：采用标号作业法，每次迭代产生一个永久标号，从而生长一颗以V0为根的最短路树，在这颗树上每个顶点与根节点之间的路径皆为最短路径。由于网络不存在负权，最短路树的生长过程中各顶点将按照距离的远近以及顶点的相邻关系，逐次长入树中。

图1 线缓冲区示意图

2 基于战时道路通行概率的最短路径模型

2.1 模型假设

通过地理信息空间几何关系中的缓冲区分析，对缓冲区内的军地油料保障力量进行分析后，查找出目标区域内的道路损毁情况，计算出每一段道路的通行概率，并以此计算出运油车前送油料的最短时间路径，以保证油料保障任务能及时顺利的完成。假设：

（1）缓冲区内至少有一条路径能够通行 （可以通过更改缓冲区半径R达到该条件）；

（2）缓冲区内各段道路损毁情况及路段长度已知；

（3）运油车在各路段上的平时行驶速度已知；

（4）弹坑的坑口都为规则的圆。

2.2 模型构建

战时道路通行概率的假设。根据现代非接触战争的特点，假设战时道路主要受到以下两个因素的影响：一是弹坑的大小及分布情况；二是道路本身损毁情况。

第一、弹坑影响下道路通行概率的计算公式为：

B为弹坑的直径大小，BC为弹坑的临界直径大小，BC=K1-K2，K1为道路的可行驶的实际宽度，K2为运油车的宽度。

第二、道路本身损毁影响下道路通行概率：

针对在敌人炸弹落在道路附近造成破坏的情况。根据道路的位置及重要性不同，遭敌袭击破坏的程度不同，战时道路损毁程度可分为四个等级，分别为基本完好、轻微破坏、中等破坏和严重破坏。可分别给不同的等级赋不同的概率值PB来表示道路的连通性。如表1所示。

表1 战时道路损毁等级描述

因此，路段的通行概率可以表示如下：

其中，PD为受弹坑影响的路段通行概率，PB为受道路本身破坏程度影响的路段通行概率，β为权值，战时情况下取β=0.7。

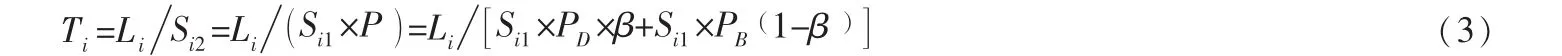
其中，Si1为运油车平时在该路段的行驶速度，Si2为战时运油车在该路段的行驶速度，Li为该路段长度除以Si2，Ti为战时运油车通过该路段所需要的时间Ti。

步履如飞，精神抖擞，思维敏捷，67岁的杨宗祥状态丝毫不输给年轻人。与很多出生于五十年代的人一样，杨宗祥的童年也是充满艰辛。13岁无奈辍学回家挣工分，17岁时，他被分到安宁洪源养殖场工作，他摸索出了鱼苗的孵化技术，当时在昆明属于领先技术。他又充分利用养殖场的资源，养鸡、养猪，自己焊鸡笼，挑鸡粪、猪粪，配饲料，直至当上了场长。

弹坑大小的分布——假设弹坑的直径大小介于0到K1之间，所以符合参数λ2=K1的指数分布：其中λ=K1，为道路的可行驶的实际宽度。且x为从战役野战油库到后方油库的道路编号1,2,3,…,n。

设在缓冲区内有n个道路节点 （包含起点后方油库和终点战役野战油库），分别为ai（i=1,2,…,n）。V0：路径起点，S：具有永久标号的顶点集，u：路径抽象途中暂未永久标号的定点，l（V）：V的标记，f（V）：V的父顶点，用以确定最短路径。为了便于计算机的计算和处理，需要将GIS相关信息数字化，系统采用邻接矩阵来表示网络图。其基本方法是：设G=（V,E）是一个无向图，V=｛v1,v2,…,vn｝， 则G的邻接矩阵A=（aij）n×n。其中：

用邻接矩阵表示图，很容易判定两个顶点之间是否有边相连，也容易求出各顶点的次数。且无向图是对称的，只考虑上三角矩阵即可。

2.3 模型求解

结合GIS中存储的道路情况计算出弹坑的分布情况和弹坑大小的分布情况，运用公式 （1）和 （2）计算出缓冲区内目标道路的通行概率P，并结合目标道路长度Li和已知的道路平时速度Si1，运用公式 （3）计算出战时运油车在路段i的通行时间Ti，输入以Ti为权的带权邻接矩阵w=［w（ vi, vj）］：

②更新 l（v）,f（v）—— 寻找不在S中的顶点u，使l（u）为最小。把u加入到S中，然后对所有不在S中的顶点v，如l（v ）＞l（u）+w（ u,v）， 则更新l（v）,f（v）,即 l（v ）←l（u）+w（ u,v）,f（v ）←u；

③重复步骤②，直到所有顶点都在S中为止。

3 模型算例

在战时，某部队油料部门从后方油库往战役野战油库前送油料。后方油库为点V1，战役野战油库为点V11，中间共有道路节点11个，22段道路，每段道路的长度已在道路网络图中标注，单位为km，抽象的道路网道路编号如图2所示。18号、11号、4号和1号道路宽度为10m，其余道路的宽度为7m，运油车的宽度为2.5m，运油车在V1→V3→V6→V9→V11的干路上的行驶速度为80km/h，在其余支路上的行驶速度为50km/h。1号道路至22号道路的里程分别为：20、90、40、60、70、10、20、90、30、10、10、30、40、10、50、20、90、80、20、60、70、10；单位为km。求前送油料的最短时间路径。

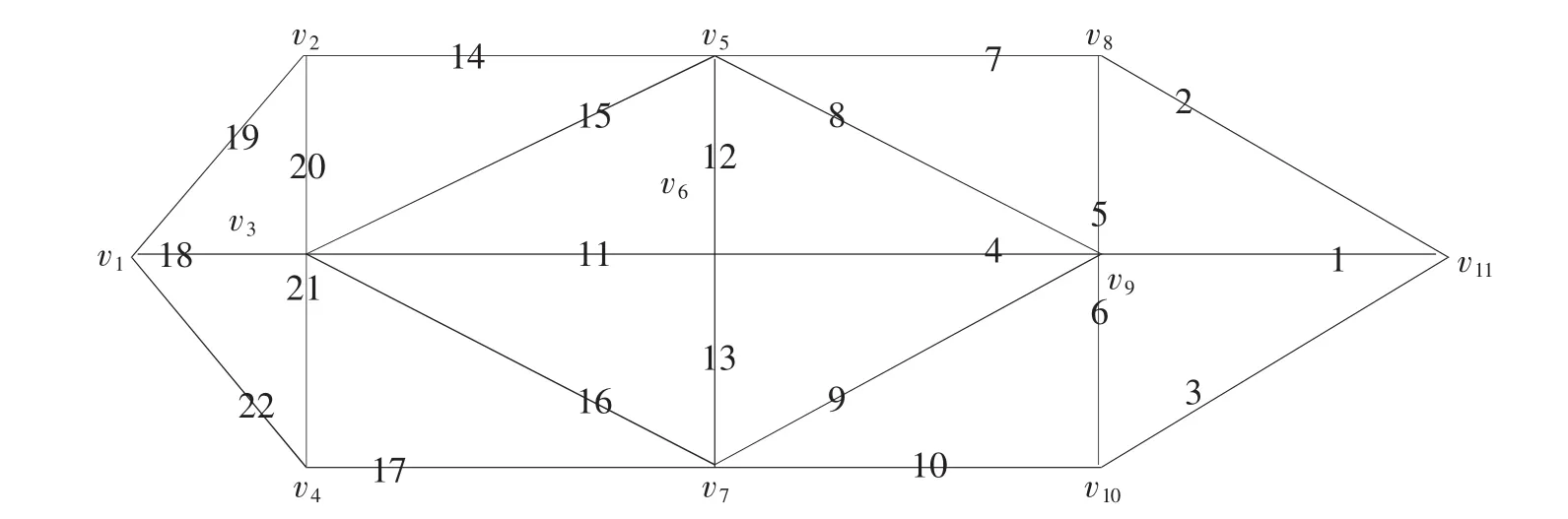
图2 抽象路网道路编号图

运用公式 （1）、（2）和 （3）求出战时运油车在编号为1至22的道路上的行驶时间分别为：0.317,2.118,0.941,0.882,1.647,0.235,0.471,2.278,0.941,0.235,0.158,0.706,0.8,0.2,1,0.4,1.8,1.266,0.4,1.2,1.4,0.2；单位为小时。将得到的时间作为抽象路网的边权，作为邻接矩阵，并用matlab编程实现得到结果如下：

即最短路路径为从点V1→点V2→点V3→点V7→点V10→点V9→点V11；最短路路径值为2.45小时，约为两个半小时。

4 结 论

本文结合缓冲区分析，根据战时目标区域内道路损毁情况，对战时运油车通行概率的模型和最短时间路线选择模型进行了分析，利用D算法求出了后勤部队油料分队从后方油库往战役野战油库前送油料的时间最短的路线，对战时油料保障有一定的指导意义。本文最大的特点是考虑了战时道路的通行概率，更加贴近实战，使油料运输分队战时油料保障更具针对性。但是在算法上还存在一些不足，需要手动输入起点、终点和路网带权邻接矩阵，计算量稍大、占用资源较多等，将在下步的研究中将进行进一步的改进。

[1]王海英,等.图论算法及其MATLAB实现[M].北京：北京航空大学出版社，2010.

[2]陈子侠,等.基于GIS物流配送线路优化与仿真[M].北京：经济科学出版社，2007.

[3]李萌.西藏军区油料保障智能决策支持系统研究[D].重庆：解放军后勤工程学院 （硕士学位论文），2006.

[4]孙卫东，殷武,等.油料管理理论与方法[M].北京：解放军出版社，2004.

[5]李军，郭耀煌,等.物流配送车辆优化调度理论与方法[M].北京：中国物资出版社，2001.

[6]姚娜,等.GIS、MapInfo与MapBasic学习教程[M].北京：北京大学出版社，2000.

[7]边文质.航炮射击弹着点的分布特性研究及试验规范的讨论[J].西安工业大学学报，1983(2)：33-47.