钢丝绳缺陷漏磁信号的通道均衡化方法

赵 敏，张东来，周智慧

(哈尔滨工业大学深圳研究生院，518055广东深圳)

钢丝绳被广泛应用于港口、电梯、矿井提升机中，是设备的关键部件，被形象地喻为“命根子”，为保证其安全可靠地工作，需要对钢丝绳的运行状况作定期检测［1］，相关的标准也已初步形成［2］.漏磁检测法是钢丝绳无损检测中最通用的方法，检测传感器主要有线圈传感器［3］、霍尔传感器［4］、磁通门传感器［5］及巨磁阻传感器［6］等，磁偶极子模型［7］、数值分析［8］、有限元方法［9］及神经网络［10］等方法在漏磁场正问题及逆问题中也得到了广泛的应用.由于传统的检测方法大多采用单霍尔或线圈传感器，检测钢丝绳的主漏磁通，其输出为一维信号，只能解析到缺陷在钢丝绳上的轴向分布，而不能得到周向分布.引入霍尔阵列传感器后，增加了周向分辨率及解析度［4］.在检测过程中，霍尔的输出结果容易受到霍尔传感器与钢丝绳之间距离［11］(即为提离距离)的波动、不同周向位置的励磁不均匀性等因素影响，即使是针对同一缺陷进行检测，霍尔传感器输出的幅值与相位也不同，此种现象称之为通道失衡.通道失衡将严重影响检测系统的性能及缺陷的定量检测［12-14］.在使用“管道猪”对管道进行检测时，由于其各个通道提离距离及励磁场强不一致，通道失衡现象严重.文献［12-14］中采用自适应滤波算法对“管道猪”的通道失衡进行抑制，取得了较好的效果.由于霍尔阵列传感器的结构与“管道猪”的极为类似，也存在通道失衡问题，但钢丝绳的表面结构与管道表面结构不同.本文结合钢丝绳的螺旋结构特点，首先对漏磁信号进行基线估计，减小漏磁信号中因提离距离波动及励磁不均造成输出的直流低频分量不均衡，再通过峰谷值检测，以某一通道峰谷值为参考，对各通道的峰谷值归一化，实现了钢丝绳漏磁信号的通道均衡化.结果表明，均衡化后的漏磁图像具有很好的缺陷检测率.

1 钢丝绳漏磁检测系统

传统的感应线圈传感器的输出为一维信号，可实现缺陷的轴向定位及断丝的初步预估，基于霍尔阵列传感器的漏磁检测系统不仅能实现缺陷轴向、周向定位，且其输出结果不受绳速影响，较感应线圈传感器有更好的性能.钢丝绳漏磁检测系统结构图如图1所示.

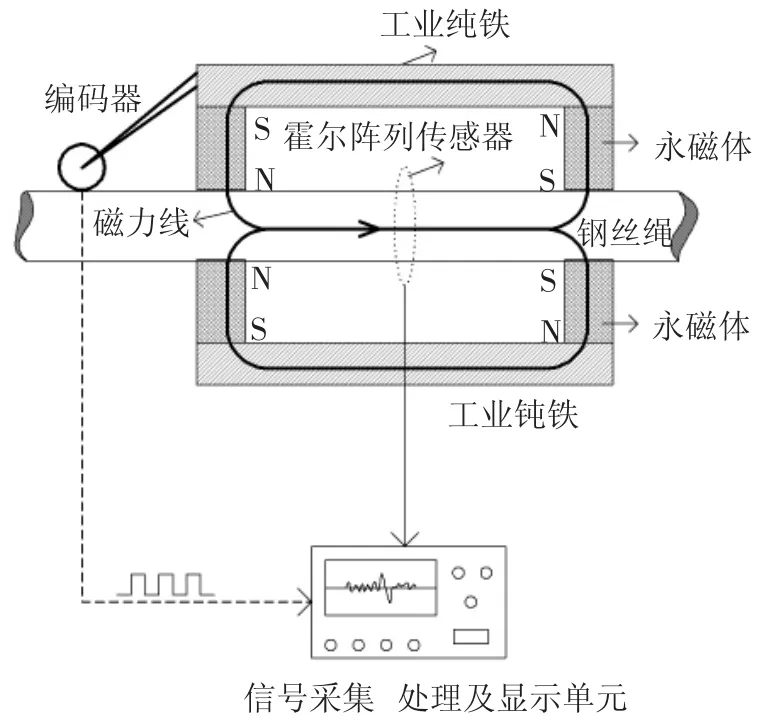
图1 钢丝绳漏磁检测系统结构图

采用永磁体及由工业纯铁制成的磁轭形成闭合励磁磁路，实现钢丝绳的饱和励磁.当钢丝绳每相对运动0.65 mm时，编码器发出一个同步脉冲给采集单元，数据采集单元采集30个霍尔通道的数据，随着钢丝绳穿过励磁机构，完成对整根钢丝绳漏磁数据的采集.基于霍尔阵列传感器的钢丝绳漏磁检测系统主要有以下3个部分组成:1)永磁励磁装置，实现钢丝绳轴向饱和励磁.钢丝绳的饱和励磁是漏磁场产生的前提，理想励磁方式为完全径向励磁，此方式励磁的磁源利用率高，且周向均匀度好.在实际应用中，多采用多回路励磁方式以提高励磁均匀度，图2所示为八回路励磁结构.2)霍尔阵列传感器，用于钢丝绳附近漏磁检测，安装在励磁装置的中间对称位置，其实物图如图3所示.3)漏磁数据采集分析系统，实现钢丝绳缺陷漏磁信号的等间隔采样及数据的在线分析，采集的霍尔阵列传感器的数据经过如图4所示的平面展开，形成缺陷漏磁图像.数据采集过程中，当钢丝绳与励磁装置之间发生相对运动时，光电编码器将产生一系列的等间距脉冲，触发控制单元对霍尔阵列传感器的数据进行采集，经过在线分析处理，实现缺陷的定位及定量.

图2 励磁装置实物图

图3 霍尔阵列传感器的实物图

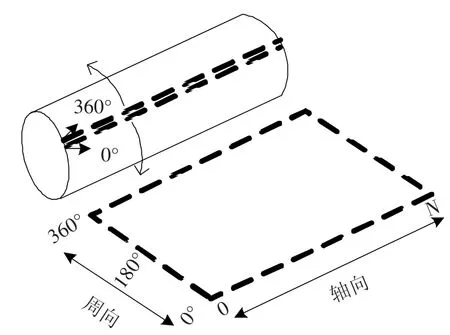
图4 检测数据展开示意图

2 漏磁信号的通道均衡化算法

在检测过程中，一方面由于励磁装置的铜套直径略大于钢丝绳直径，霍尔阵列传感器中的各个霍尔元件将有不同的提离值，另外一方面，励磁装置为多回路永磁体拼接组成，钢丝绳的周向励磁强度失衡，导致霍尔阵列传感器的各不同通道输出有不同的直流偏置及不同的交流幅值.

如图5所示，本文的通道均衡方法主要步骤如下:1)基线消除.因提离距离及励磁不均等因素造成的输出直流低频波动为漏磁信号的基线，采用分段平均法，消除漏磁信号中的基线，分段数据的数目为一个股波周期内的采样数据数目;2)峰谷值提取.查找因钢丝绳的绳股及缺陷形成的漏磁场的交流信号幅值波动范围;3)峰谷值归一化.以某一通道的峰谷波动平均值为参考，用其他通道与参考通道的比值对各个不同的通道的峰谷值波动进行补偿，将峰谷值的波动范围归一化.图6为霍尔阵列传感器的原始输出数据，由图可见，30个霍尔通道数据存在较大的相异性，通道失衡严重.图7为其中某两路霍尔通道的输出，可以看出其信号的直流偏置及峰峰值波动都存在一定的差距.

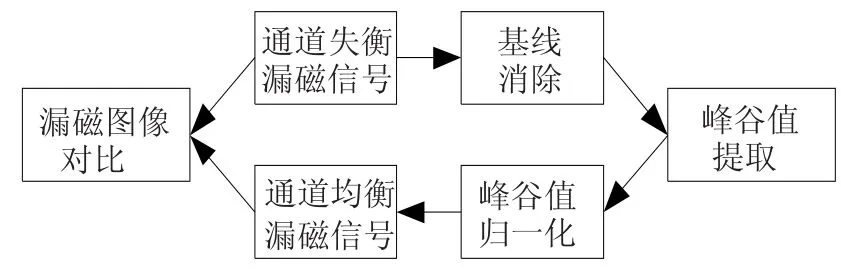
图5 通道均衡化流程图

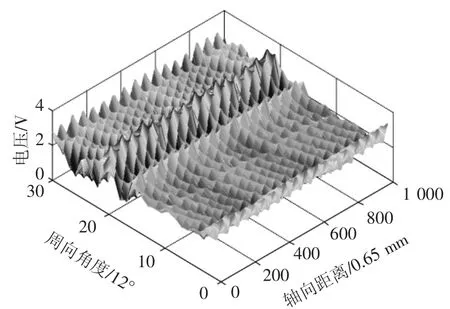
图6 霍尔阵列传感器的原始输出

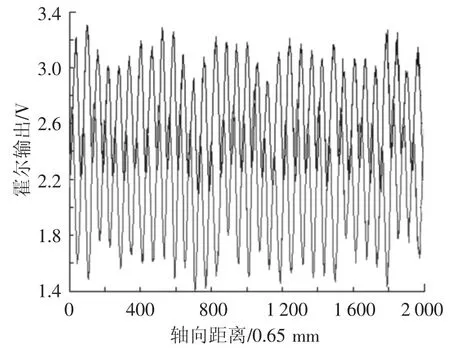
图7 两个不同通道霍尔的输出

2.1 漏磁信号的基线消除

霍尔阵列传感器中采用的霍尔元件型号为A1321，在零磁场时，其直流偏置输出为Vs/2，Vs为霍尔元件供电电压.假设单个霍尔元件的输出为y(t)，则有

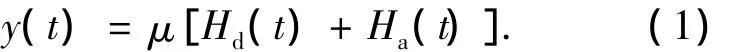
式中:μ为霍尔系数，Hd(t)为在当前提离值下的励磁场场强，Ha(t)为缺陷及钢丝绳绳股的漏磁场场强.提离距离的波动将造成励磁场强的波动，漏磁信号的基线就是此波动影响的结果.

基线估计的方法是采用分段平均法，由于钢丝绳为螺旋对称结构，绳股所产生的漏磁信号类似正弦信号，在一个周期内的平均值趋近0，因此，分段平均的数据数目n的值由式(2)确定.

式中Ds为钢丝绳股距，d为等空间采样间隔.

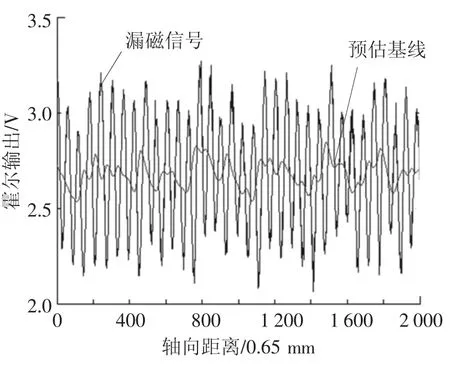
图8 漏磁信号的基线估计

图8为基线估计的结果，预估出的基线所表示的是由于背景励磁磁场及提离距离波动等造成的漏磁信号波动.通过式(3)消除漏磁信号的基线:

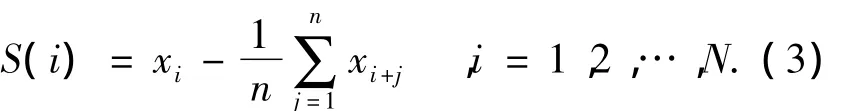
式中:S(i)为基线消除后的漏磁信号，xi为当前数据，N为采集数据总数.

2.2 通道均衡化

经过基线消除后，由于提离距离及励磁不均等因素影响造成的低频噪声得到了很好的抑制，而上述因素对式(1)中的Ha(t)部分的影响还需要做进一步的归一化.其归一化的过程是提取漏磁信号的峰谷值后，以某一通道数据为基准对其他通道的峰谷值进行归一化.漏磁信号的峰谷值提取算法流程如下:

1)设置查找峰值标志位F1，当其为1时，在检测数据中查找峰值，为0时，在检测数据中查找谷值;

2)设峰值Mx的初始值为-inf，谷值Mn的初始值为inf，峰谷值的阈值为δ;

3)检测数据的当前值为Di，判断当前值Di是否大于峰值Mx，若为真，则令Mx=Di，否则，Mx保持不变;

4)判断当前值Di是否小于谷值Mn，若为真，则令Mn=Di，否则，Mn保持不变;

5)若F1为1，则判断Di是否小于Mx-δ，若为真，则令Mn=Di，否则，Mn不变，修改F1为0;

6)若F1为0，则判断Di是否大于Mn+δ，若为真，则令Mx=Di，否则Mx不变，修改F1为1;

7)判断当前数据是否为最后一个数据，若否，则获取下一个数据，重复3)～6)，直到完成所有数据的检测判断.

图9为峰谷值检测结果，设峰谷值的平均值为Vi，以通道1为基准，可通过式(4)对(3)式中的S(i)进行修正，修正后的数据为S'(i)，且

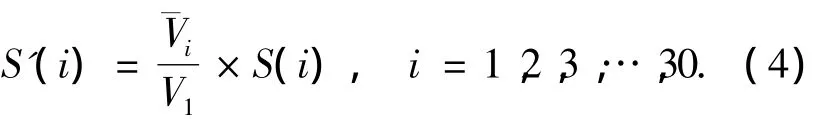
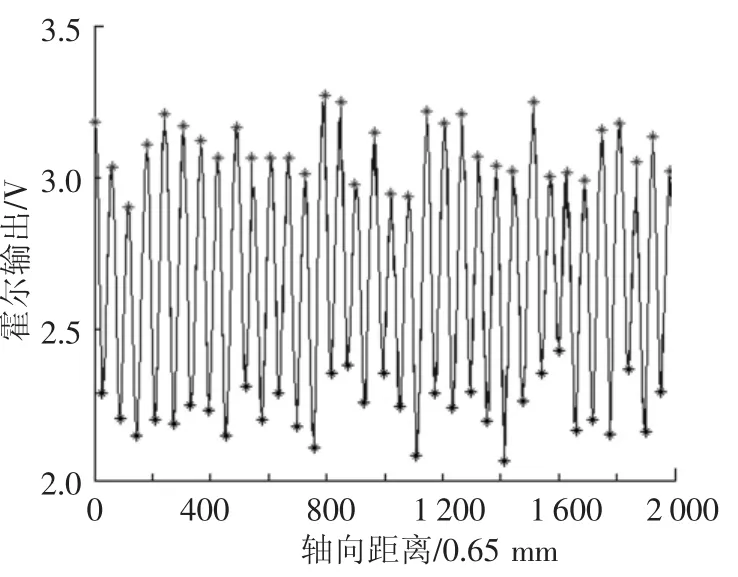
图9 漏磁信号的峰谷值检测

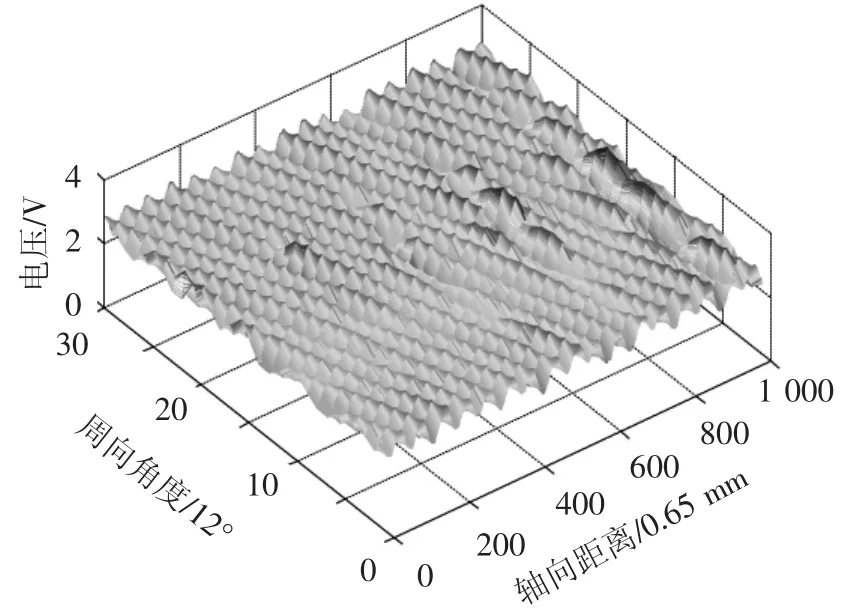
图10 通道均衡化后的霍尔通道数据

在同一钢丝绳的轴向及周向不同位置制作7个缺陷，采集其漏磁数据，图11为采集的原始漏磁图像数据，图12为通道均衡后的漏磁灰度图像，图11中可明显看到两条较亮的线条，是因漏磁不均造成的信号通道失衡痕迹，经过通道均衡后，图像的对比度及缺陷区域的清晰度都得到了明显的提升.标准方差是衡量整体数据中个体间的离散程度，对于通道均衡前后的漏磁图像，采用标准方差来衡量均衡化前后漏磁图像的均衡度.均衡化前的漏磁图像的标准方差为0.064 7，均衡化后为0.020 8，均衡化后的漏磁图像的对比度及缺陷区域的可见度得到了较大提高.

图11 通道均衡化前的漏磁灰度图像

图12 通道均衡化后的漏磁灰度图像

分析两幅漏磁图像的股波纹理的方向特征，将均衡化前后的两幅图像使用Roberts交叉梯度算子f进行掩模滤波，

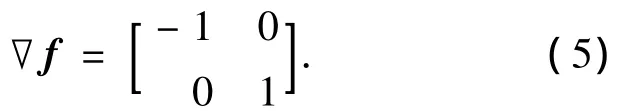
得到的滤波图像如图13～14所示.

图13 通道失衡漏磁图像的滤波图像

图14 通道均衡漏磁图像的滤波图像

经过统计分析及阈值分割，结果显示:经过通道均衡化的漏磁图像，检出缺陷为7处，与实际所做缺陷数相符，而通道失衡的漏磁图像，仅检出2处缺陷.经过多组实测数据的验证，均衡化的漏磁图像的缺陷的检测准确率远高于通道失衡的漏磁图像.

3 结论

1)相对于传统的一维漏磁信号，使用霍尔阵列传感器捕获钢丝绳表面沿周向、轴向漏磁场的三维分布，可以为缺陷的定量检测提供更加全面的信息.

2)在漏磁检测中，传感器提离距离波动与励磁强度不均匀性是导致各个不同霍尔通道数据产生相异性的根本原因，采用有效的方法补偿提离距离波动及励磁不均匀性对漏磁场的影响，可以有效地提高漏磁信号的信噪比.

3)本文采用漏磁信号基线预估的方式减小由提离距离波动及励磁不均所造成的低频及直流噪声，结合钢丝绳漏磁信号的固有特征，对不同通道数据的峰谷值进行归一化处理，使各霍尔通道实现了均衡化，提高了缺陷漏磁图像的对比度及信噪比.

4)通道失衡的漏磁图像中，缺陷区域都淹没在股波背景噪声中，而均衡化后的漏磁图像缺陷区域清晰，提高了缺陷检测准确率.

［1］杨叔子，康宜华.钢丝绳断丝定量检测原理与技术［M］.北京:国防工业出版社，1995:5-10.

［2］武新军，康宜华，杨叔子.无损检测在役钢丝绳标准的研究［J］.起重运输机械，1999(2):33-36.

［3］WEISCHEDEL H R.The inspection of wire ropes in service:a critical review［J］.Materials Evaluation，1988，46(5):430-437.

［4］CAO Yinni，ZHANG Donglai，WANG Chao，et al.More accurate localized wire rope testing based on hall sensor array［J］.Materials Evaluation，2006，64(9):907-910.

［5］GU Wei，CHU Jianxin.A transducer made up of fluxgate sensors for testing wire rope defects［J］.IEEE Transaction on Instrumentation and Measurement，2002，51(1):120-124.

［6］SINGH W S，RAO B P C，VAIDYANATHAN S，et al.Detection of leakage magnetic flux from near-side and far-side defects in carbon steel plates using a giant magneto-resistive sensor［J］.Mea-surement Science and Technology，2008，19(1):1-8.

［7］DUTTA S M，GHORBEL F H，STANLEY R K.Simulation and analysis of 3-D magnetic flux leakage［J］.IEEE Transactions on Magnetics，2009，45(4):1966-1972.

［8］SNARSKII A A，ZHENIROVSKYY M，MEINERT D，et al.An integral equation for the magnetic flux leakage method［J］.NDT＆E International，2010，43:343-347.

［9］戴光，徒芸，杨志军.基于三维有限元动态模拟圆柱形表面腐蚀缺陷漏磁场［J］.无损检测，2007，29(1):2-5，8.

［10］田志勇，张耀，谭继文.基于BP神经网络的钢丝绳断丝定量检测［J］.煤炭学报，2006，31(2):245-249.

［11］崔伟，黄松岭，赵伟.传感器提离值对管道漏磁检测的影响［J］.清华大学学报:自然科学版，2007，27(1):21-24.

［12］ZHANG Yong，YE Zhongfu，XU Xu.An adaptive method for channel equalization in MFL inspection［J］.NDT＆E Interna-tional，2007，40(2):127-139.

［13］MUKHERJEE D，SAHA S，MUKHOPADHYAY S.An adaptive channel equalization algorithm for MFL signal［J］.NDT＆E International，2011，45:111-119.

［14］AFZAL M，UDPA S.Advanced signal processing of magnetic flux leakage data obtained from seamless gas pipeline［J］.NDT＆E International，2002，35:449-457.