捷联惯性/星光折射组合导航算法

钱华明，孙 龙，黄 蔚，蔡佳楠

(哈尔滨工程大学自动化学院，150001哈尔滨)

惯性/天文组合导航系统(SINS/CNS)作为一个黄金组合系统一直以来受到各国的高度重视.其组合方式一般分为简单组合方式和基于最优估计的组合方式.前一种组合方式简单、可靠，但是精度较低.目前基于最优估计的组合导航系统主要有两类:1)基于校正惯导陀螺漂移的SINS/CNS组合导航系统［1-3］;2)基于高度角和方位角直接敏感地平的组合导航系统［4-6］.第一种组合导航系统是利用星敏感器获取高精度的姿态信息，将SINS与星敏感器的姿态差作为量测，通过滤波器估计陀螺漂移.这种方式能够较好的修正由陀螺漂移引起的姿态误差，但是由于对加速度计误差估计不准确，不能阻止速度和位置误差的发散.而第二种方法由于地球表面不规则，使得地平仪或惯性平台提供水平基准的测量精度较低，这与星敏感器的测量精度不匹配，极大的影响了系统的定位精度.

20世纪80年代发展起来的基于星光折射间接敏感地平的方法能够有效的解决地平敏感精度不高的问题.它结合大气对星光的折射模型，利用高精度星敏感器精确敏感地平，从而实现高精度定位［7-10］.国内外对此进行了大量的理论研究，并进行了实验验证.研究结果表明:这种方法成本低廉、结构简单，能达到较高的精度，是一种很有前途的导航方法，目前在30 km的高空飞行器上已经实现应用［11］.

本文提出将捷联惯导与星光折射间接敏感地平的天文导航方法相结合，组成捷联惯性/星光折射组合导航系统(SINS/RCNS)，并将其应用于高空长航时无人机.该导航系统是一种完全自主的系统，完全满足长航时无人机对隐蔽性的要求.而且由于无人机飞行高度一般在20 km以上，观测星体比较容易.同时在20～50 km范围的大气层内大气以水平运动为主，该层大气稀薄，不含水蒸汽，大气成分比较稳定.所以大气模型的建立比较简单，本文使用文献［10］提出的大气折射模型来进行理论研究，并对所建立的导航模型进行实验验证.

1 组合导航原理

如图1所示，当恒星星光高度较低时，星光在穿越地球表面大气层时会发生折射.折射后的光线向内弯曲，导致恒星的视位置比真实的位置偏高.使用星敏感器和精确的大气折射模型可得到星光折射角，从而精确敏感地平，进行高精度的导航定位.

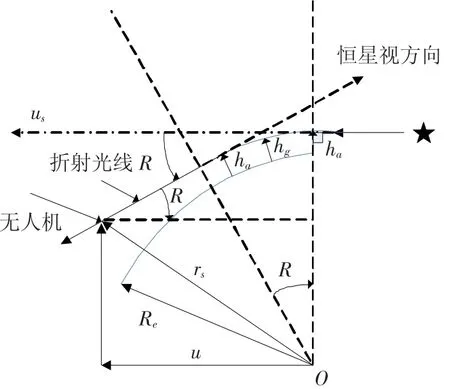
图1 星光折射几何图示

大气折射模型的精度影响着导航的精度，其影响的程度甚至超过了星敏感器，研究结果表明:当星光折射单一导航，大气密度精度高于1%时，位置、速度的估计误差均方差与大气密度精度按线性规律变化［12］对于大气折射模型的研究，文献［10］改进了现有的大气密度模型和固定高度(25 km)的观测模型，建立了一种连续高度的星光折射观测模型:

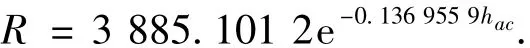
其中R为星光折射角(″)，由此得到折射高度为

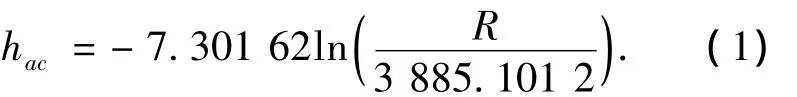
式中hac单位为km.

SINS/RCNS组合导航系统需要两个星敏感器.星敏感器a对准不发生折射的恒星.通过观测结果确定出未折射的星光矢量在载体本体坐标系的坐标P1和载体的姿态角，由此可修正由惯导陀螺漂移引起的姿态误差，抑制位置和速度误差的发散.星敏感器b对准折射星，由观测值可以确定出折射后的星光方向矢量在本体坐标系中的坐标P2.如图2所示，由P1和P2可得到两恒星星光之间的角距θ2，它与由恒星星历查得的标称值θ1不同，二者的差值就是星光折射角(此处忽略了星敏感器a的误差，认为由星历查得的恒星矢量us1与星敏感器测量得到的P1相同，且两个角度求差值的时候转换到了同一坐标系下).

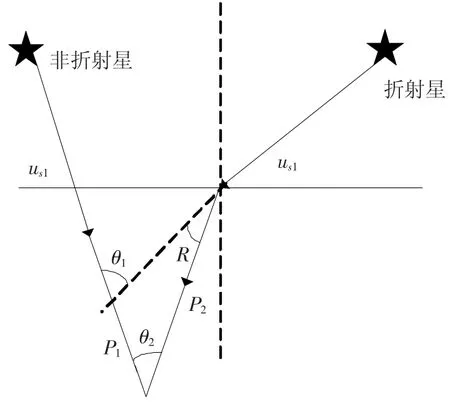
图2 星光折射角示意图

得到星光折射角R后，通过公式(1)可以得到新模型星光的折射高度hac，同时由图1所示的几何关系也可得到

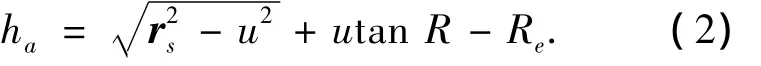
其中

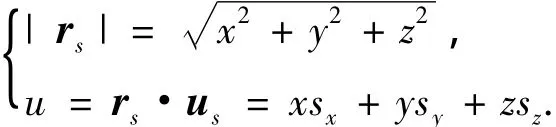
式中:x，y，z分别是位置矢量在地心惯性系下的坐标;sx，sy，sz分别是折射前恒星的单位方向矢量在地心惯性系下的坐标，通过查找星历得到.折射高度的观测量反应了载体与地球之间的位置关系，因此可以利用其修正惯导加速度计偏置引起的导航误差.

2SINS/RCNS系统数学模型

2.1 系统状态方程

无人机的状态方程由平台失准角误差、速度误差、位置误差组成［12］:

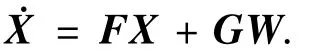
状态变量X=［Φδvδrε］T，其中Φ=［φxφyφz］为平台失准角误差;δv=［δvEδvNδvU］为东向、北向、天向速度误差;δr=［δφ δγ δh］分别为纬度误差、经度误差和高度误Δ差;εΔ=［ΔεxεΔyεz］为陀螺随机常值漂移;=［xyz］为加Δ速Δ度计Δ随机常值偏置;误差量W=［εsxεsyεszsxsysz］T分别为陀螺仪和加速度计的随机噪声.

2.2 组合导航量测方程

SINS/RCNS组合导航量测方程由两部分组成:1)姿态误差量测;2)折射高度误差量测.

2.2.1 姿态误差量测

姿态误差角由惯导输出的姿态角βⅠ，θⅠ，αⅠ与星敏感器输出姿态角βX，θX，αX之差得到，表达式为

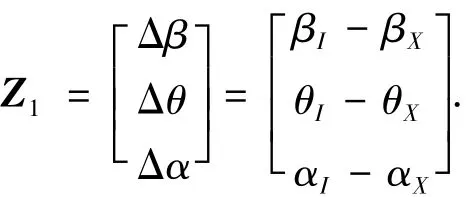
上式得到的是姿态误差角，而状态方程中使用的是平台误差失准角.在很多研究中，常常将二者视为相等，但实际上二者并不完全相等.本文采用文献［13］的思想推导姿态误差角和平台误差角的关系，并使用泰勒展开略去二阶小量得到姿态误差量测的线性方程为

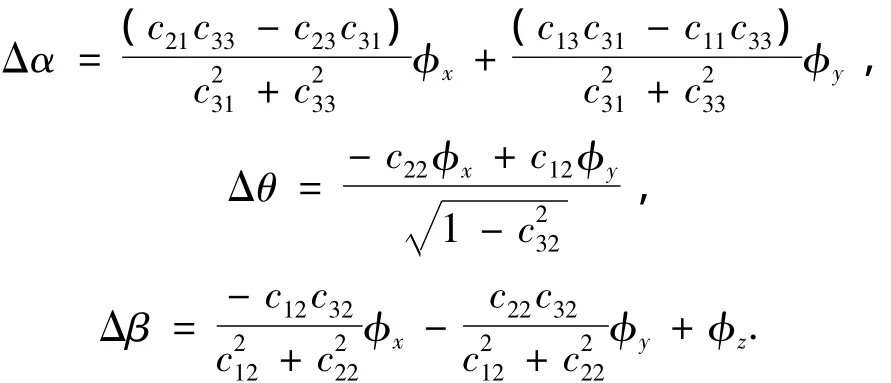
其中cij来自载体系到地理系的转换矩阵Cnb:

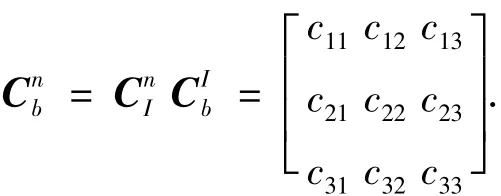
其中CⅠb为载体系到惯性系的转换矩阵，由星敏感器测得;Cn

Ⅰ为惯性系到地理系的转换矩阵.

因此得到姿态误差角的量测方程:

式中v1为星敏感器的测量误差.

2.2.2 折射高度量测

式(2)中，rs和u中含有跟地球有关的位置参数，必然包含惯导惯性器件产生的位置误差.而对

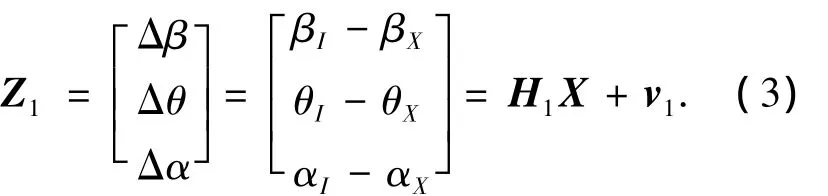
其中于式(1)，只要大气折射模型足够精确就可以认为是不含有位置误差的理论值.考虑理想情况，假设大气折射模型足够精确，因此将单位统一化后定义折射视高度误差为

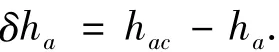
由式(2)得

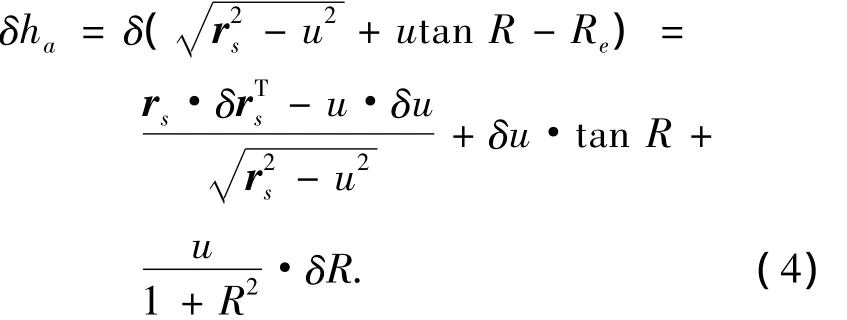
定义导航坐标系为地理坐标系，而量测方程中跟状态变量相关的参数都是地心惯性系的，所以要将其中参数转换到地理系.定义地心惯性系到地球坐标系转换矩阵为CEⅠ.由图1得，航天器的位置矢量rs=h，h为地理坐标系中距地心的天向矢量，且有｜h｜=h，则位置矢量在地球坐标系的坐标为

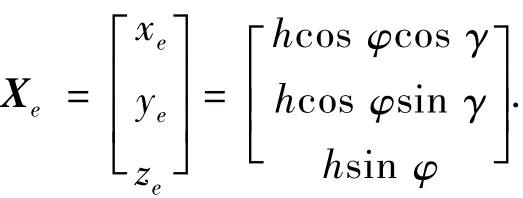
由XⅠ=CⅠEXe=(CE)-1Xe得

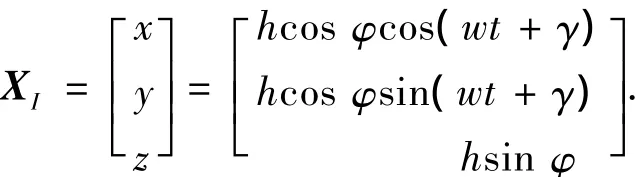
由上式可求得惯性系中的位置误差为

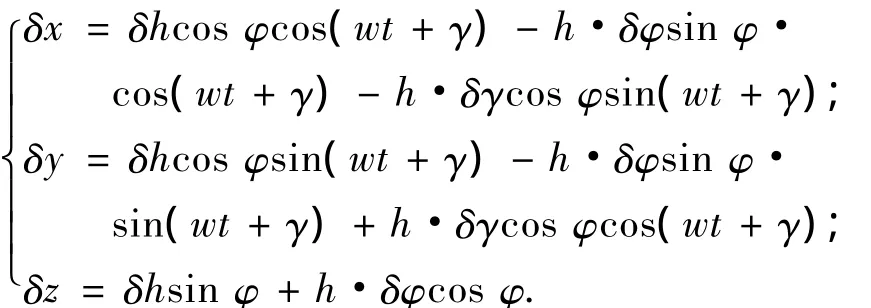
式(4)中各参数计算如下:

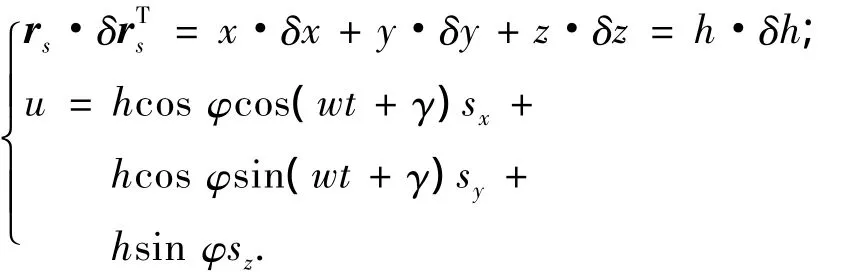
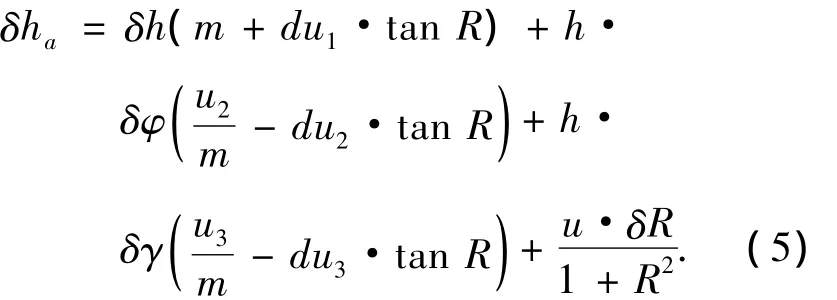
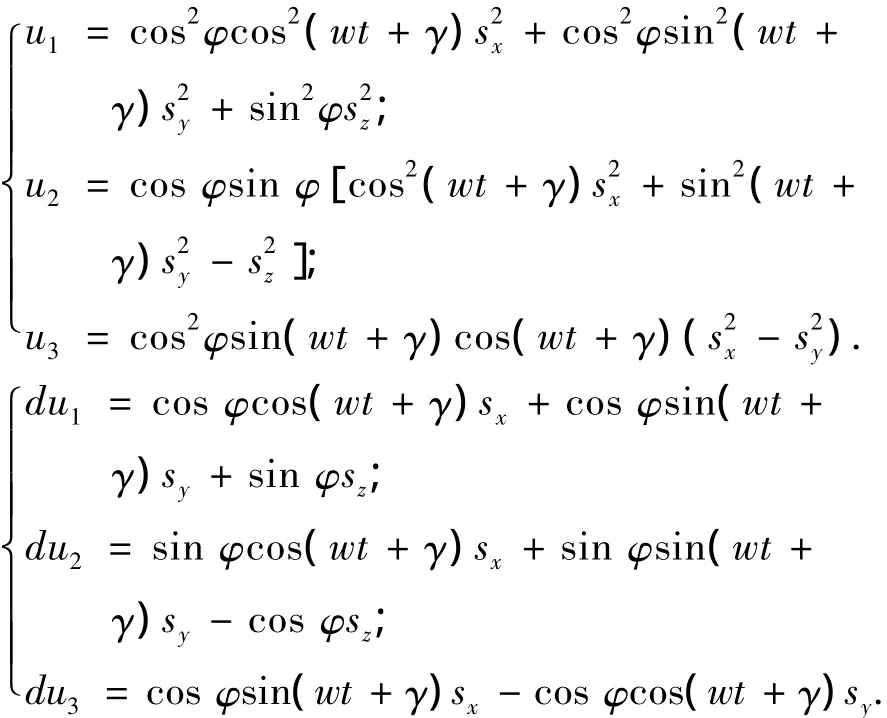
将u代入式(5)最后一项，将其作为量测误差:

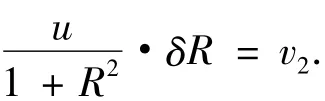
则基于星光折射的量测方程为

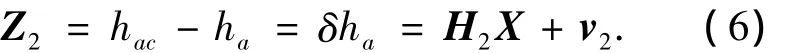
由式(3)和式(6)可得到系统总的量测方程为

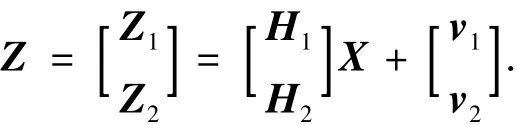
2.3 组合导航系统导航精度分析

大气折射模型的精度影响着导航的精度，而影响大气折射模型精度的主要因素是大气密度的准确程度.文献［12］中分析指出:通过研究，可以将平流层大气密度随纬度和季节变化的部分进行修正，有可能使平流层大气密度的估计误差小于1%.而1%的大气密度误差将导致63.7 m的航天器位置误差.使用星光折射方法进行导航，理论上可以达到63.7 m以内的定位精度.而直接敏感地平的方法，因为地平模型的不准确性导致定位误差为几百米乃至上千米［4-6］，由此可见星光折射敏感地平法比直接敏感地平法具有较大优势.

系统的可观测性决定了卡尔曼滤波的精度，文献［14］对传统的基于校正惯导陀螺漂移的SINS/CNS组合导航系统进行了可观测性分析.文中指出，可观测度最好的状态变量是陀螺漂移，其次是平台失准角，其余的状态变量可观测度都很小，可视为不可观测.用文献［14］的方法对基于校正惯导陀螺漂移的SINS/CNS组合导航方法和本文方法进行对比分析，两种方法的状态变量对应的奇异值如表1所示.

由表1可以看出:本文方法在传统法基础上增加了与位置误差相关的折射高度后，大部分原来不可观测的状态变量对应的奇异值变大，可观测的系统状态维数明显增加，系统总体的可观测性有很大提高，则系统状态经过卡尔曼滤波的精度相比于传统法有明显提高.

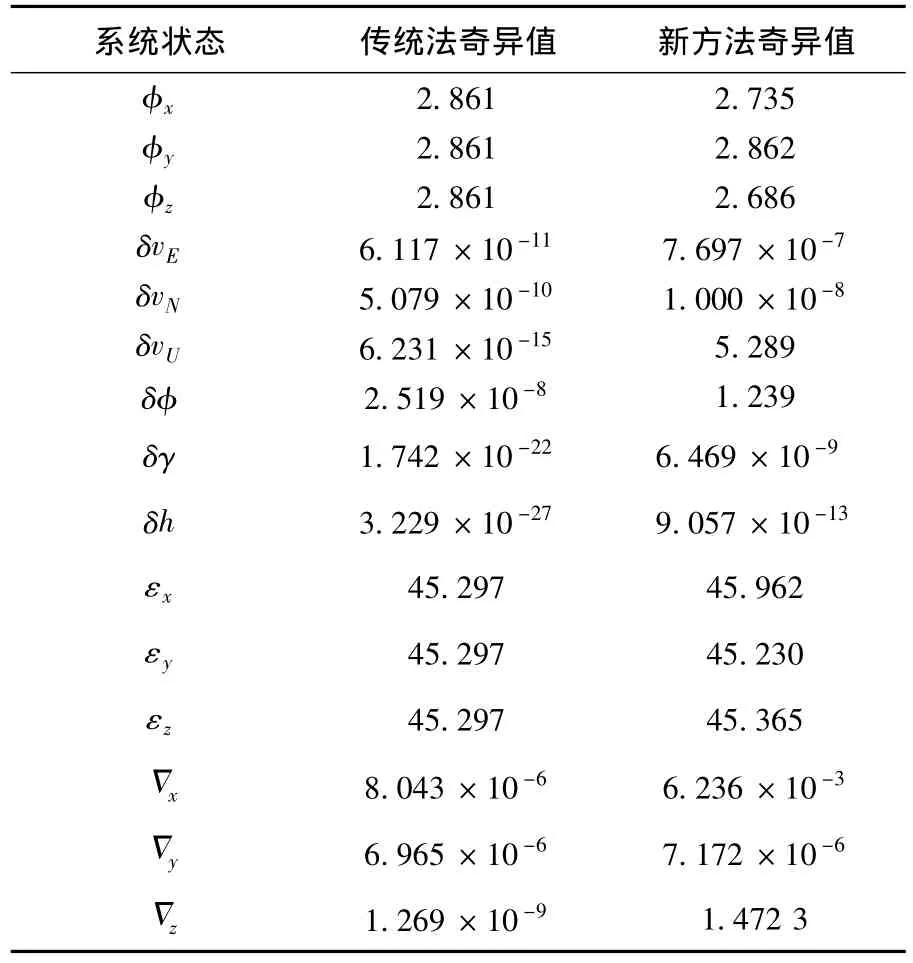
表1 本文方法和传统法状态对应的奇异值

3 仿真与分析

仿真初始条件:无人机初始位置东经120°北纬36°.经过加速爬升、平直飞行、倾斜转弯、俯冲等一系列过程，飞行时间3 500 s.飞行轨迹如图3所示.

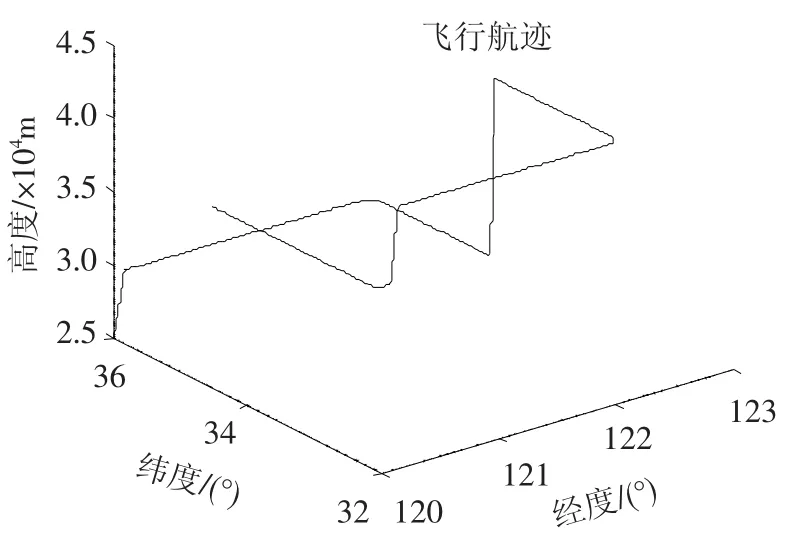
图3 无人机飞行轨迹

初始参数设置:陀螺常值漂移和随机漂移分别为0.1°/h和0.05°/h;加速度计常值和随机偏置分别为20 μg和10 μg;星敏感器精度5″(1σ);地平仪测量精度0.02°(1σ).3种方法的导航误差统计如表2所示，仿真曲线如图4和图5所示.其中新方法代表本文提出方法;方法二代表基于校正惯导陀螺漂移的SINS/CNS组合导航方法;方法三代表基于高度角和方位角直接敏感地平的组合导航方法.

表2 导航误差统计(3σ)

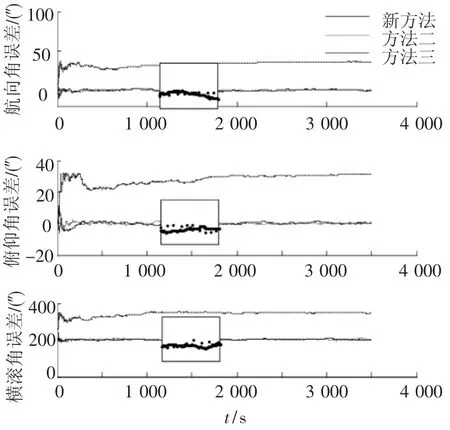
图4 姿态误差对比曲线

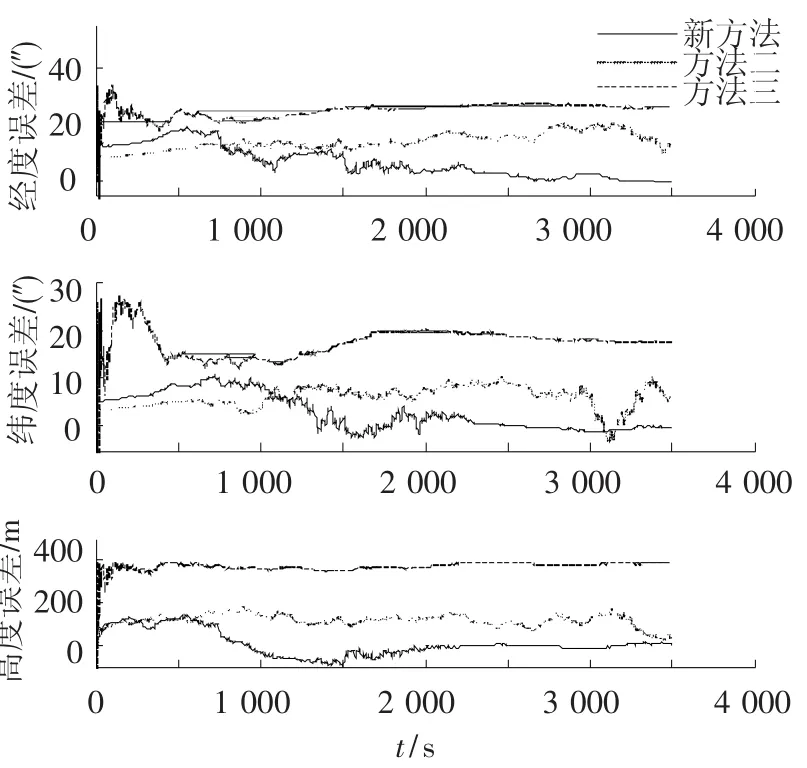
图5 导航误差对比曲线

仿真结果表明:本系统与传统的修正陀螺漂移SINS/CNS组合导航系统相比，二者的姿态误差基本一样，仍然保持了星敏感器测姿的高精度特性，总体姿态角误差都优于3″.而本系统由于在量测中增加了与位置误差相关的折射高度，进一步抑制了惯导速度和位置误差的发散，导航位置误差在3″以内，传统的修正陀螺漂移法位置误差却达到十几秒，对比优势明显.与传统的高度差法相比，姿态和导航精度更是提高了接近一个数量级，优势更加明显.

4 结论

SINS/RCNS组合导航系统由于在量测中增加了与导航位置误差相关的折射高度，相较于传统的基于校正陀螺漂移的SINS/CNS组合导航系统，能够进一步抑制速度和位置误差的发散.同时跟传统基于高度差法的SINS/CNS组合导航系统相比，由于星光折射间接敏感地平的精度高，弥补了与星敏感器精度不匹配的缺陷，导航精度得到了显著提高.

针对SINS/RCNS的研究都是在理想情况下进行的，下一步的研究方向是建立SINS/RCNS组合导航系统的实际导航模型，包括无折射星和有折射星情况的处理、根据星敏感器视场研究选星的限制条件、新滤波方法的应用等.

［1］JAMSHAID A，FANG Jiancheng.Realization of an autonomous integrated suite of strapdown astro-inertial navigation systems using unscented particle filtering［J］.Computers and Mathematics with Applications，2009，57(2):169-183.

［2］XU Fan，FANG Jiancheng.Velocity and position error compensation using strapdown inertia lnavigation system/celestial navigation system integration based on ensemble neural network［J］.Aerospace Science and Technology，2008，12(4):302-307.

［3］JAMSHAID A，FANG Jiancheng.SINS/ANS integration for augmented performance navigation solution using unscented Kalman filtering［J］.Aerospace Science and Technology，2006，10(3):233-238.

［4］熊智，刘建业，郁丰，等.基于天文角度观测的机载惯性/天文组合滤波算法研究［J］.宇航学报，2010，31(2):397-403.

［5］屈蔷，刘建业，熊智.结合天文观测角量测的机载惯性/天文深度组合算法［J］.南京航空航天大学学报，2011，43(6):765-769.

［6］裴福俊，居鹤华，崔平远.基于天文与速度联合观测的月球车自主导航方法［J］.宇航学报，2009，30(2):486-491.

［7］WANG Xinlong，MA Shan.A celestial analytic positioning method by stellar horizon atmospheric refraction［J］.Chinese Journal of Aeronautics，2009，22(3):293-300.

［8］周凤岐，赵黎平，周军.基于星光大气折射的卫星自主轨道确定［J］.宇航学报，2002，23(4):20-23.

［9］李琳琳，孙辉先.基于星敏感器的星光折射卫星自主导航方法研究［J］.系统工程与电子技术，2004，26(3):353-357.

［10］王国权，金声震，孙才红，等.卫星自主导航中25～60公里星光大气折射模型研究［J］.科技通报，2005，21(1):106-109.

［11］曾威，崔玉平，李邦清，等.惯性/星光组合导航应用与发展［J］.飞航导弹，2011(9):74-79.

［12］房建成，宁晓琳.天文导航原理及应用［M］.北京:北京航空航天大学出版社，2006:185-203.

［13］宁晓琳，蔡洪炜，吴伟仁，等.月球车的惯性/天文组合导航新方法［J］.系统工程与电子技术，2011，33(8):1837-1844.

［14］吴海仙，俞文伯，房建成.高空长航时无人机SINS/CNS组合导航系统仿真研究［J］.航空学报，2006，27(2):219-224.