具有落角约束的弹道导弹再入末制导律设计
2013-09-02魏鹏鑫荆武兴高长生
魏鹏鑫,荆武兴,高长生
(哈尔滨工业大学航天工程系,150001哈尔滨)
当弹道导弹进入再入飞行段对目标进行打击时,不仅要求导弹能够精确地命中目标,还对其落角提出了要求.这是因为在现代战争中一些重要的打击目标通常都会借助山体等地形屏障作为防护,只有弹头的落角(也有文献称碰撞角)满足一定的条件时,才会在最大的程度上杀伤目标[1].因此,具有终端碰撞角的再入末制导律得到了国内外学者的重视和研究.
传统的制导律(如比例导引律及其变形)主要是保证脱靶量尽量达到最小,并没有对终端落角提出限制.文献[2]基于对比例导引理论的研究,通过改变时变比例系数来满足末段角度的约束.但该制导律也存在着比例导引律固有的问题,如终端时刻过载出现奇异,没有弹道修正能力等.近些年来,国内外许多文献提出了各种各样满足碰撞角约束的制导律,其中大部分制导律都是针对二维平面中的单个角约束的.文献[3]基于最优控制理论中的线性二次型框架来描述这个问题,Ryoo对导弹动力学模型进行一系列简化,以能量最小为指标计算了恒速导弹闭环形式的控制指令解;文献[4]采用目标跟踪滤波器预测机动目标信息,提出了基于最优控制理论的终端角约束制导律;文献[5]基于最优控制和微分对策理论提出了角约束制导律;文献[6]提出了一种基于状态依赖Riccati方程的终端角约束制导律;文献[7]提出了一种基于滑模控制技术的具有碰撞时间和碰撞角约束的制导律.但采用上述方法设计的制导律或者采用了线性化假设,或者需要借助于外部设施在线计算制导指令.
模型预测静态规划技术(Model Predictive Static Programming,MPSP)是最近几年发展的一种新的技术[8-10],它是基于模型预测控制和静态规划理论发展起来的.该方法的特点是对于一类最优控制问题(协态向量与系统输出同维),可以成功地将动态规划问题转化为静态规划问题,因此可以使得计算效率更高.这种方法通过解整个时间段的协态向量来更新控制变量解.因为协态向量的解析解可以求出来,所以该方法可以获得闭环形式的最优控制解.而且,求解协态向量的系数矩阵可以通过递归方法求出,这大大地节省了计算时间,避免了最优控制理论的数值计算复杂性问题.MPSP技术本质上是将一个弹道最优化的概念引入到制导律中来获得一个既能满足终端打击精度限制又能满足终端碰撞角限制的设计方法.MPSP技术的主要优点在于:并没有对非线性动力学模型采用线性化假设,并且能节约更多的能量.与大多最优控制方法类似,MPSP制导律同样也需要知道制导指令加速度的初始猜想解.
本文首先简要地介绍了模型预测静态规划技术的基本原理;其次,建立了导弹三维运动以及目标平面运动模型,并基于PN及APN制导律设计了制导指令的初始猜想解;然后,基于MPSP技术设计了具有落点和落角约束的弹道导弹再入段末制导律;最后,针对弹道导弹打击地面静止目标、慢移动目标以及机动目标进行了数值仿真,并将其与增广比例导引律进行了比较,验证了该制导律的优越性.
1 模型预测静态规划理论
模型预测静态规划技术是Indian Institute of Science大学Padhi教授[11]近几年提出的一种基于模型预测控制和静态规划理论发展起来的新的技术.本节将要对该理论进行简单的描述.
一般的MIMO非线性系统模型的表达形式如下:

其中X∈Rn,U∈R,Y∈R.将系统模型方程用离散形式表达如下:

式中k=1,2,…,N-1表示时间步数标号,N为终止的时间步数.MPSP方法的主要目标是获得一组合适的控制变量Uk,使得在终止时间步数的输出YN达到期望输出值YNd.而且,使用最小的控制能量来完成这个目标.对于这种MPSP方法,需要给出一组控制变量的预测猜想值.当然,这组预测的控制变量并不一定能满足YN→YNd的目标.MPSP方法就是计算这组预测猜想值的偏差,然后与当前的控制变量值做差,来获得1个更优的控制变量解,使得这组预测猜想控制变量值会随着迭代的进行而快速地更新.这种迭代更新的过程持续进行,直到YN→YNd的目标完成.
首先,将YN在YNd处进行泰勒展开,并忽略高阶项,可以得到输出误差如下:

式中等号右边的方括号表示YN相对于XN在时间步数N处的偏导数.根据式(1),在时间步数k+1处的误差为

其中dXk和dUk分别是状态变量和控制输入在第k步的小误差向量.将dUN如式(3)(令k=N-1)一样展开,并代入到式(2)得
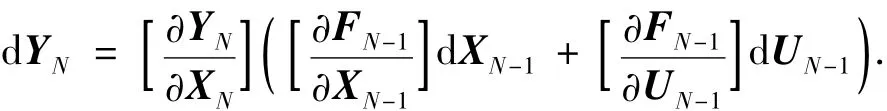
同理,将状态变量在第N-1步的误差dXN-1按照式(3)展开为第N-2步的状态变量及控制变量的形式,然后,再将dXN-2展开为包含dXN-3和dUN-3的形式,以此类推,直到k=1,可以得到如下方程:
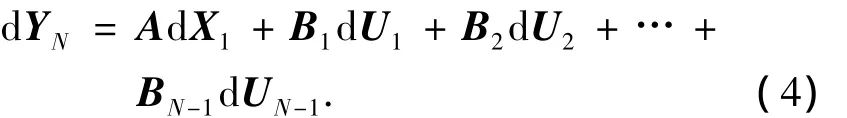
式中系数矩阵A和Bk的表达式如下:

其中k=1,2,…,N-2,因为状态变量的初始条件假设为确定的值,则第一步的状态变量的误差为零,即dX1=0.因此式(4)变为
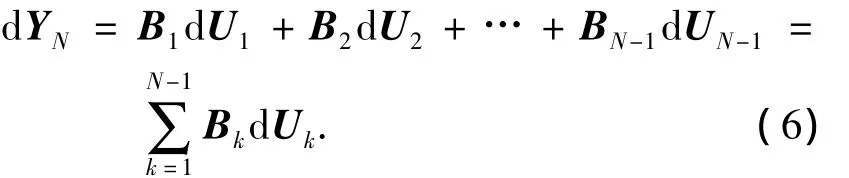
注意到上式中矩阵Bk可以通过如下的递归方法计算出来,这可以极大地降低MPSP算法计算的复杂性,有效地提高了制导律计算的效率.首先,定义B0N-1如下:

然后按照下式求出矩阵B0k和Bk:

注意到式(6)中含有(N-1)m个未知变量和p个方程,且通常p≪(N-1)m,故以式(6)作为系统的约束方程,通过建立如下性能指标函数来获得最优控制解:
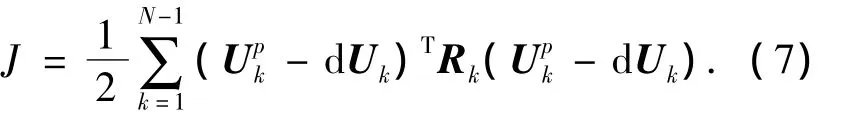
其中Upk表示先前的控制变量解,dUk为对应的控制变量解的偏差,Rk为正定的权重函数,需要由设计者进行合理地选取.MPSP方法设计的主要目的是在方程(6)的约束下,使得式(7)中的性能指标函数最小.根据限制条件下的静态优化理论[12]及文献[8]中的推导可以得到
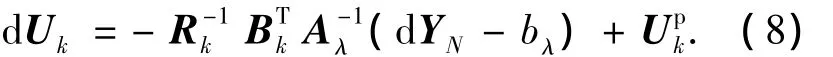
其中λ为协态向量.因此在时间步数k=1,2,…,N-1处的更新的控制变量为

式中:

MPSP方法的创新性在于可以获得很高的计算效率,主要由以下因素影响的:1)与最优控制理论的两点边值问题相比,这种方法仅仅要求1个与状态变量同维的协态向量λ,就可以获得更新的控制变量;2)协态向量有符号解析解,因此,控制变量更新值也有符号解析解;3)计算这个符号解所需要的系数矩阵Bk可以通过递归方法计算出来.因此,这种MPSP方法的计算效率很高,对于在线实现具有一定的应用前景.通过设置输出收敛精度值终止算法以及在特定的时间步长内仅仅进行有限次的迭代更新,也可以提高计算效率.上述已经给出了该种方法的基本思想,性能指标函数的形式并不局限于式(7)的表达式,在应用的过程中,可以根据不同的问题选择不同的指标函数并采用与之对应的算法.
2 弹道导弹和目标的运动学模型
2.1 弹道导弹三维动力学模型描述
将弹道导弹考虑为一个质点,并且考虑气动力、重力以及自动驾驶仪延迟的影响,得到导弹的动力学及运动学微分方程如下所示[13]

其中θm和ψm分别表示弹道倾角和弹道偏角,其他符号的定义参看文献[13].假设弹道导弹自动驾驶仪模型为一个一阶传递函数,则实际的加速度可以表示为

其中τ为自动驾驶时间延迟系数,ayc和azc分别代表y向和z向(速度坐标系)的指令横向加速度.因此,本文的研究中,在产生制导指令时,分别用ayc和azc来代替式(10)中的y和z;在进行数值仿真时,分别用ay和az来代替式(10)中的y和z,这样做的目的是验证系统在存在自动驾驶仪延迟时仿真结果的有效性.惯性坐标系下弹道导弹与目标几何关系如图1所示.
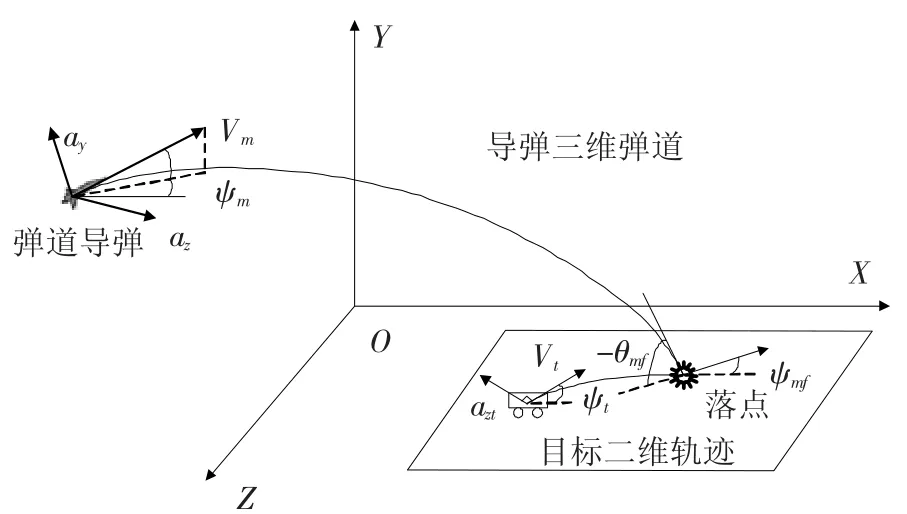
图1 三维仿真场景示意图
图1中弹道导弹打击的目标为1个具有二维机动能力的目标,弹道倾角θm、弹道偏角ψm及终端落角-θmf、ψmf的描述如图1所示.值得注意的是,因为弹道导弹打击的是地面目标,所以终端落角θmf为负值.两个制导指令出现在式(10)中θm和ψm的动力学方程中.其中制导指令ay作用在俯仰平面(XOY)上,az作用在偏航平面(XOZ),且均垂直于速度矢量.为了保证所有状态变量具有类似的数值变化范围,将这些状态变量进行标称化:

其中第二个下标n表示标称化后的变量,上标*表示各变量标称化所用到的标准比较值,一般取值得注意的是,应该合理地选择这些标准比较值,才能保证各个标称化变量的最大值及最小值的范围基本相同.将式(10)标称化,并写成矢量的形式:

式中:

下面基于上节提出的MPSP方法,构造使得终端脱靶量及落角满足一定约束的制导律算法.首先采用欧拉积分方法将对象的动力学模型进行离散化:

下一步定义终端时刻(k=N)的期望输出向量为一个5×1的列向量,该列向量前两个元素为标称化的终端时刻的落角,另外三个元素为标称化的终端时刻的位置坐标.假设目标的坐标位置信息(xt,0,zt)已知(下一小节将具体给出该处目标的动力学模型),将式(11)对Xk求导,可得

式中

进一步求Fk对Uk的偏导数为
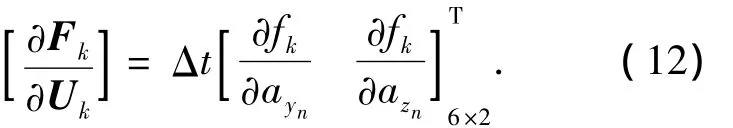
根据式(11)可得输出向量Yk对Xk的偏导为

2.2 目标二维动力学模型描述
弹道导弹的打击目标可以选为地面静止目标、慢移动目标以及机动目标(如航空母舰等).在推导目标动力学模型时,假设目标为一个速度恒定的质点,其横向加速度指令azt垂直于它的速度Vt.对于弹道导弹制导系统,目标的位置、速度是已知的,将目标的机动加速度等效为一个可以粗略探测到的不精确值与在这个不精确值基础上的扰动项.并且对于弹道导弹,粗略探测的不精确值是已知的,而横向加速度的“扰动值”是未知的.进一步,假设加速度的扰动形式可以用正弦曲线Asin(ωt)(其中A=0.08,ω=1 000,A表示横向加速度的扰动上确界为0.08g)来描述,则目标的运动模型可以用如下式表示:
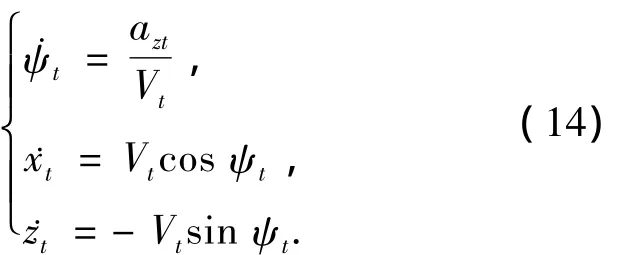
为了与弹道导弹模型一致,将式(14)进行标称化得到
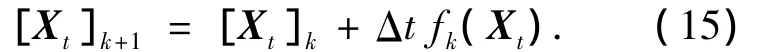
式中:

式(15)用来产生目标的坐标位置,以便进一步计算dYN.横向加速度azt用来描述目标的机动形式.
3 基于MPSP方法的具有落角约束的再入末制导律设计
3.1 基于扩展比例导引律的猜想控制解的计算
本文采用扩展的比例导引律来计算初始的猜想控制解.下面简要介绍猜想控制解的求解过程.首先定义σ为导弹与目标的三维视线旋转角速率:
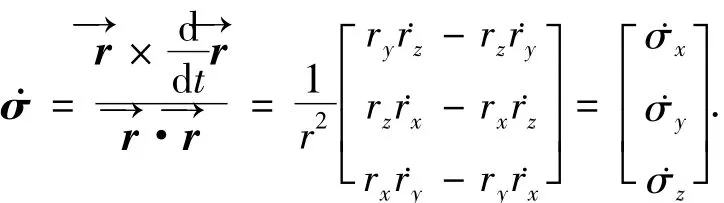
式中最右侧的向量表示视线角速度在惯性坐标系下的分量,且rx,ry和rz分别表示弹目距离在惯性系下的分量.接下来,将视线旋转角速度转换到速度坐标系下,可以表示为


假设导引律比例系数为Ne,则根据增广的比例导引律(Augmented Proportional Navigation,APN)计算俯仰偏航通道的指令加速度为

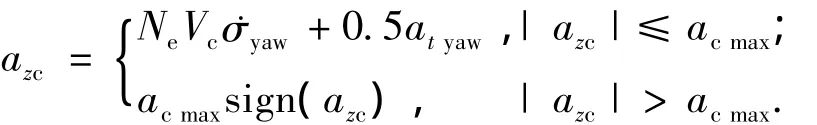
式中acmax表示加速度的限制幅值,ayc和azc表示横向加速度的指令值,通过一阶延迟环节作用于导弹动力学模型.atpitch和atyaw的表达式如下所示[11]:

3.2 基于MPSP方法的制导律的实现
MPSP制导算法的本质是基于一个猜想控制解对制导指令加速度的解进行持续迭代更新的过程,直到所得到的输出结果收敛于期望输出.可以通过判断dYN的模值或其中的元素是否小于设定的门限值来判断输出结果是否收敛.这个所设定的门限值体现了对终端脱靶量及终端两个落角的约束.下面将给出在每一个制导周期内,MPSP算法的基本步骤:
1)对于机动目标采用APN制导律计算猜想控制解,对于静止目标采用PN制导律计算猜想控制解.这一步将给出飞行时间tf和终端时刻步数N.
2)基于计算的猜想控制解采用四阶Runge-Kutta方法对导弹状态变量微分方程进行积分,这一步对应着MPSP方法的预测模块.
3)计算输出状态YN,因为期望输出YNd是已知的,所以偏差dYN也可以求出.如果dYN大于设计者设定的门限值,则进入下一步,否则退出循环,采用该收敛控制解作为制导律的指令控制信号.
4)结合式(5),(12)和(13)采用递归的方法计算系数矩阵Bk,k=N-1,N-2,…,1.
5)计算Aλ和bλ.
6)根据式(8)和(9)计算dUk和新的控制解Uk,然后回到第2)步.这一步对应MPSP算法的纠正模块.
具体流程如图2所示,注意到该方法采用Euler算法进行递归运算,采用4阶Runge-Kutta方法对仿真场景进行预测计算,这两种算法的结合虽然损失一定的计算精度,但却有效地减少计算时间.尽管Euler方法的计算精度没有RK4方法的计算精度高,但是采用Euler方法可以获得一个很好的离散动力学模型,而且其中的系数矩阵的计算效率更高.通过在一个制导周期内合理地选择的迭代次数,也可以进一步减少计算时间.

图2 基于MPSP方法的制导律实现流程
4 仿真算例分析
本小节将给出考虑终端弹道倾角和弹道偏角约束情况下的多组仿真结果.为了验证MPSP制导律在针对不同运动形式的目标的有效性,本文的仿真分析包括了不同类型的场景算例,且每种算例都考虑了自动驾驶仪的时间延迟.选取权重矩阵为单位矩阵,即RK=I2×2.仿真参数如表1所示.注意到在打击地面机动目标的仿真场景中,目标的机动加速度假设受到一干扰加速度的影响,其实际的真实加速度对于导弹制导系统来说是未知的.下面具体分析各个场景下的仿真结果.

表1 仿真参数设置表
4.1 仿真场景1:打击地面静止目标
本小节主要通过仿真分析研究弹道导弹如何以期望的碰撞角和小的脱靶量打击地面静止目标,仿真结果如表2和图3至图4所示.根据仿真结果可知,脱靶量小于1 m.图3给出了相同初始条件、不同终端落角约束下采用MPSP技术的弹道轨迹曲线,在所有的案例中,终端脱靶量均小于1 m.图4给出了同样初始条件不同落角约束情况下的弹道倾角θm和弹道偏角ψm变化曲线.选取判断终端落角是否收敛的阈值为0.4,可以看出该算法的收敛时间随着终端角约束值偏离基于PN制导律所获得的终端角的程度增加而增加.这是因为,如果期望值偏离猜想控制值越大,MPSP算法更新控制解的迭代次数会更多.因此,在约束条件θmf=-80°时的收敛时间要大于θmf=-45°,而在约束条件θmf=-80°时的导弹打击捕获区域要小于θmf=-45°.

图3 同样初始条件、不同落角约束情况下的导弹三维弹道轨迹

图4 弹道倾角θm和弹道偏角ψm的响应曲线
4.2 仿真场景2:打击地面机动目标
在本小节中,假设地面目标做正弦机动,机动加速度的形式为

为了增加仿真的多样性,仿真条件取为:

图5表示采用APN和MPSP制导律的导弹与目标的三维弹道轨迹图的局部放大图,图6表示制导指令的响应情况,具体的详细结果如表2所示.从图6可以看出,采用APN制导律的制导指令响应呈正弦形式波动,而采用MPSP制导律的制导指令近似于单调形式,可以节省更多的控制能量,并且执行机构更加易于跟踪制导指令,受目标机动加速度幅值和频率影响更小.
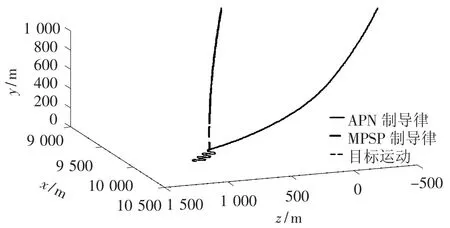
图5 地面机动目标和弹道导弹的三维弹道轨迹的局部放大图

图6 制导指令的响应曲线

表2 针对目标的不同约束条件下的仿真结果
5 结论
为了保证弹道导弹在末制导段能够从各个空域方向打击目标,本文基于模型预测静态规划技术,设计了具有落角和落点约束的三维再入段末制导律.得到的结论如下:
1)这种制导律不仅可以满足落点和落角的约束,还可以使在整个再入飞行场景中控制能量(即横向机动加速度)较小.
2)这种制导律具有在线快速优化弹道的能力,对初始条件的要求更为宽松,有着较大的打击捕获区域.对打击静止和机动目标都很有效.
3)与其他具有落角约束的制导律相比,该制导律并没有对非线性运动模型采用线性化假设,且其计算复杂性明显低于基于最优控制的终端角约束制导律.
基于模型预测静态规划技术研究具有落角约束的制导律是一个很复杂的问题,目前的工作仍然是初步的,基于理论层次的,在制导律的设计中有许多工程化的因素尚未考虑.下一步的研究工作将在考虑更多工程化因素的情况下,针对更为真实的末制导场景设计更易于工程实现的制导律,并完成这种算法收敛性的理论证明.
[1]胡锡精,黄雪梅.具有落点和落角约束的圆轨迹制导律[J].宇航学报,2012,33(5):562-569.
[2]KIM B S,LEE J G,HAN S H.Biased PNG law for impact with angular constraint[J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(1):277-288.
[3]RYOO C K,CHO H,TAHK M J.Optimal guidance laws with terminal impact angle constraint[J].Journal of Guidance,Control,and Dynamics,2005,28(4):724-732.
[4]SONG T,SHIN S,CHO H.Impact angle control for planar engagements[J].IEEE Transactions on Aerospace and Electronic Systems,1999,35(4):1439-1444.
[5]SHAFERMAN V,SHIMA T.Linear quadratic guidance laws for imposing a terminal intercept angle[J].Journal of Guidance,Control,and Dynamics,2008,31(5):1400-1412.
[6]RATNOO A,and GHOSE D.SDRE based guidance law for impact angle constrained trajectories[C]//Proceedings of the AIAA Guidance,Navigation and Control Conference and Exhibit.Hilton Head,SC:AIAA,2007:1-16.
[7]HARL N,BALAKRISHMAN S.Impact time and angle guidance with sliding mode control[C]//Proceedings of the AIAA Guidance,Navigation and Control Conference and Exhibit.Chicago,IL:AIAA,2009:1-22.
[8]PADHI R,KOTHARI M.Model predictive static programming:a computationally efficient technique for suboptimal control design[J].International Journal of Innovative Computing,Information,and Control,2009,5(2):399-411.
[9]MAITY A,PADHI R.MPSP Guidance of a Solid Motor Propelled Launch Vehicle for a Hypersonic Mission[C]//Proceedings of AIAA Guidance,Navigation and Control Conference.Minneapolis,Minnesota,2012:1-23.
[10]DWIVEDI P N,BHATTACHARYA A,PADHI R.Suboptimal Midcourse Guidance of Interceptors for High-Speed Targets with Alignment Angle Constraint[J].Journal of Guidance,Control,and Dynamics,2011,34(3):860-877.
[11]HARSHAL B O,PADHI R,A nonlinear suboptimal guidance law with 3D impact angle constraints for ground targets[C]//Proceedings of AIAA Guidance,Navigation and Control Conference.Toronto,Ontario Canada,2010:1-25.
[12]BRYSON A E,HO Y C.Applied optimal control[M].New York:Wiley,1975:110-125.
[13]IMADO F,KURODA T,TAHK M J.A new missile guidance algorithm against a maneuvering target[C]//Proceedings of the AIAA Guidance,Navigation,and Control Conference and Exhibit.Boston,MA:[s.n.],1998:145-153.
