逆向迭代的点阵式充气翼三维保形分析

王长国，刘远鹏，崔宇佳，谭惠丰

(哈尔滨工业大学复合材料与结构研究所，150080哈尔滨)

充气翼作为一种典形的充气结构，由于结构设计时要考虑到其气动外形，其内部柔性约束较多，比普通的充气结构的构型更为复杂，因此其形状设计很关键.但是，因为充气翼膜结构分析，是典形的大变形非线性问题，要是直接以气动性能设计出的充气翼进行加工，在加载后则会产生变形，这样就与设计的构型有较大的误差进而影响气动性能，所以有必要根据充气翼目标构型寻找其未加载时的初始形态.这种根据目标构型寻找充气翼初始构型的问题在力学中是一个“逆问题”.本文把这种通过逆向迭代来寻找充气翼初始形态以确保充气翼充气加载后具有所设计的气动外形的方法定义为充气翼保形分析.此外，充气翼保形分析，对后期充气翼曲面展平、裁剪、拼接等成形过程有着重要的意义.

充气翼属于充气膜结构，其基本的形态分析方法主要有力密度法、动力松弛法和非线性有限元法.力密度法将大变形几何非线性问题化简为线性来处理，主要针对建筑索网结构提出一种初始形态分析.动力松弛法起初是用于解决潮汐流动的计算问题，在后来的研究工作中，才将流体运动方程和连续性方程改为在固定结构中的有阻尼运动方程以及材料的弹性方程，这样才使该方法应用到其他一般领域中，如初始形态分析中.而非线性有限元法求解初始构型较其他方法更为精确、效率更高，被广泛的应用于膜结构找形中，主要体现在充气膜结构和地面张拉索膜结构中.在充气膜结构找态分析中，毛丽娜等［1］运用非线性有限元的方法对天线充气膜结构的形态进行了分析;王鹏等［2］也采用非线性有限元方法对ETFE充气气枕的形态进行了分析;江锡虎等［3］运用有限元软件ANSYS对充气膜结构初始形态进行了非线性有限元分析.而在地面张拉索膜结构中，赵冉等［4］采用非线性有限元方法对深圳宝安体育场屋盖索膜结构进行了找形与找力分析;朱丙虎等［5］也采用有限元方法对上海世博会世博轴索膜结构进行了找态分析;向新岸等［6］以一种考虑二维变形的改进的非线性力密度法对上海2010年世博轴屋盖超大形张拉索膜结构进行了分析;清华大学袁驷等［7］对张拉膜结构的形态分析进行了研究，提出了一套基于非线性有限元算法的迭代求解算法.在国外，V.Stavrev［8］将形状优化技术应用于空间建筑膜结构的形态分析与设计.W.J.Lewis等［9］对涡轮叶片的形态进行了分析，为振动特性等其他分析建立模型.但目前来说，有关研究充气翼形态分析的资料不多，而充气翼的研究［10-12］主要集中在气动特性和静力承载等方面，特别在目标构型确定的情况下寻找充气翼初始形态的三维保形分析方面的资料更为有限，所以有必要对充气翼进行三维保形分析，以实现对充气翼结构的精细化设计和分析.本文提出一种逆向迭代充气翼三维保形分析方法，在有限元软件ANSYS平台上，采用大变形非线性有限元技术和APDL参数化设计语言实现对点阵式充气翼进行保形分析，高精度的寻找充气翼的初始形态.

1 三维保形分析方法

逆向迭代分析的基本思想是以目标构型为初始形，应用真实的材料参数和荷载及边界约束条件进行逆向迭代分析.通过分析，将获得变形后的几何构型与目标形进行对比，如果形状误差(均方根误差RMS)不满足要求，则修改初始几何构型，重新分析，如此迭代若干次后，可得到满足精度要求的结果.

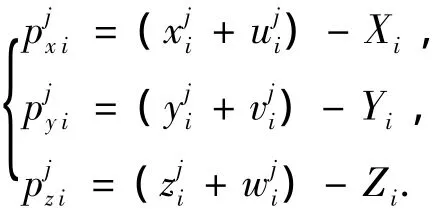
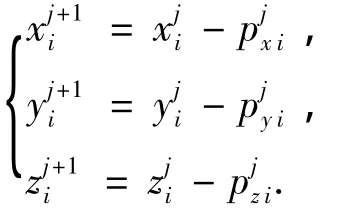
节点i在第j步变形后位置与目标节点位置的位移偏差可以表示为

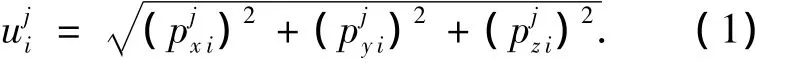
这样第j模型的位移偏差的均方根值可以表示为

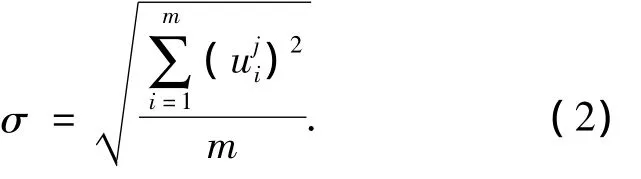
其中:式(1)为控制单节点最大变形;式(2)为控制全局节点的整体变形.

三维保形分析步骤如下:

1)以优化目标作为初始形建立三维点阵式充气翼有限元模型，然后设置蒙皮材料及内部悬拉索材料属性并划分有限元网格.

2)设置悬臂梁式边界条件，充入一定的充气压力，进行充压后非线性大变形分析，获得充压后的机翼三维变形结果.

3)处理充压分析的数据，获取充气变形后与目标机翼形状位移偏差量，并分析其均方根值RMS是否满足要求，如果满足要求，跳出循环，将所建模型作为优化结果输出.

4)如果上步RMS不满足要求，则优化节点坐标并更新模型，重复步骤2)和步骤3)，直到分析所得RMS满足精度要求，停止循环.

5)将满足RMS精度要求的最终三维模型作为结果输出.

2 三维点阵式充气翼初始形态分析

本文的研究对象是一种新型的充气翼——点阵式充气翼，其依靠内部一系列悬拉索结构来控制翼型，这些悬拉索阵列排布，机翼充气膨胀蒙皮表面会形成类似“点阵”分布的结构形态，其半翼展长为1.5 m，弦长为0.6 m，机翼根梢比为1，其目标形如图1所示.

图1 点阵式充气翼模型结构

由于该种索膜结构在ANSYS Multiphysics中计算不易收敛，所以本文在以显示积分进行运算的ANSYS LS-DYNA模块中进行分析.该充气翼蒙皮模型采用Shell 163三角形单元，悬拉索采用Link 160杆单元，材料参数如表1所示.

表1 材料参数

对模型一次充压200 Pa变形如图2所示.由一次充压变形图可以看到，该种点阵式充气翼在充压加载后，在其蒙皮表面有鼓包出现，这是点阵式约束的充气结构的典型特点.

图2 点阵式充气翼一次充压变形云图

经过9次优化，RMS满足要求，值为0.001 878 m，其RMS随优化迭代次数的变化关系如图3所示.

从图3的数据可以看出，在第1次充气后RMS超过4.3 mm，这样的偏差在结构中不能忽略，所以本文必须对模型进行保形分析，来找到满足精度条件下充气翼未充气时的构型.从图3中还可以看到充气翼每次优化并充气加载后，RMS越来越小，节点位置越来越接近该点的目标位置，而且RMS收缩速度很快，精度很高.横截面上初始形与目标形的变化如图4所示，可以看到对本文优化后的初始形进行加载后其外形与本文设计的标准形的非常接近，因此该种分析方法所得的初始形精确有效.

图3 每步优化RMS的变化

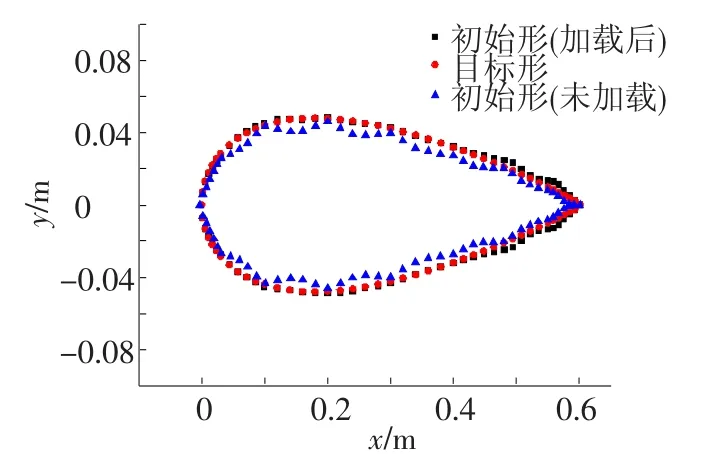
图4 机翼横截面初始形与目标形的对比

3 三维点阵式充气翼构型测试

由于点阵式充气翼属于充气结构，充气膨胀具有明显的大变形和几何非线性问题，所以传统的接触式构型测试方法不适宜.因此，本文采用Leica T-Scan激光跟踪仪对充气翼进行非接触三维构型进行扫描测试.Leica T-Scan激光跟踪仪具有70 000点/s的数据采集能力，空间长度测量误差不超过50 μm，是曲面测量、模具制造和逆向工程等方面应用的有力工具.

将点阵式充气翼连接好气压计，对充气翼中充入200 Pa的充气压力，然后将充气翼进行固定，防止其在测试过程中位置发生变化.然后对所研制充气翼模型进行跟踪扫描，如图5所示.

图5 点阵式充气翼三维构型非接触测试

获取充气翼三维形面数据点，选取了能够代表该翼面结构的3 000个数据点拟合成曲面，并与点阵式充气翼目标型进行对比，如图6所示.

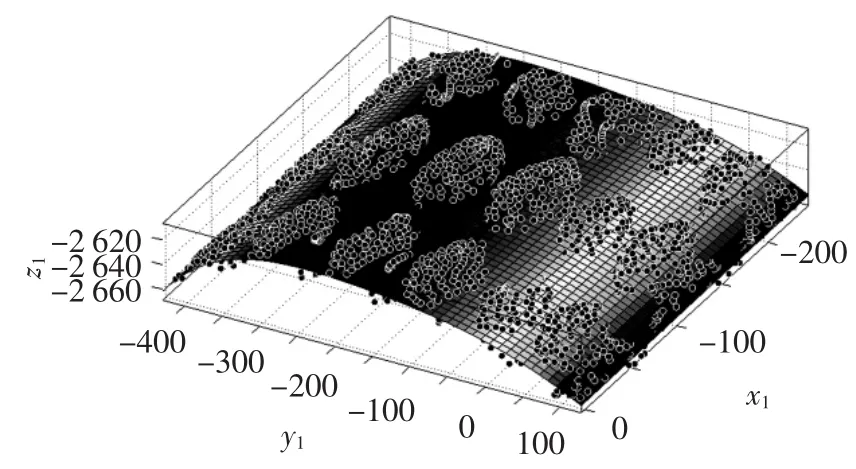
图6 数据点拟合曲面与目标型对比

形面精度的分析，用测试获得的三维形面数据点与目标平面之间误差的均方根值RMS来表示.根据试验点的三维坐标，运用曲面插值方法，在标准形上获取对应的标准点，然后做差对比，获得点云偏差的均方根值RMS.经过数据分析，试验获得的点阵式充气翼的形面精度RMS为3.05 mm.

最终获得的点阵式充气翼形面精度的实验值与通过计算的理论值存在的绝对误差约1.23 mm，有下列几方面产生:1)在裁剪机裁剪时，裁片拼接热合过程中，由于材料受热收缩以及手工操作等也会产生一定的误差;2)测试过程中充气压力不稳定也会导致被测模型构型变化，进而产生误差.通过分析误差可知，误差的主要组成部分是形态分析获得的RMS，从而证明初始形态分析可以降低形态分析过程中的形面精度RMS，直接关系到充气翼成型后的形面误差，本文提出的逆向点阵式充气翼三维保形方法是行之有效的.

4 结论

1)本文所提出的逆向迭代法可实现对点阵式充气翼三维保形的高精度分析，该方法可运用APDL参数化语言嵌入ANSYS平台得以实现.

2)本文对1.5 m尺度点阵式充气翼进行了三维保形分析，分析结果显示出逆向迭代法可高效的获取初始形，仅1次迭代其RMS就可以减小42%，仅4次迭代分析就可以获得相对稳定的RMS，说明本文的逆向迭代法具有良好的收敛性和高收敛率，并通过对点阵式充气翼进行非接触三维构型测试，得到RMS的实验值与理论值基本相符，说明了本文的逆向迭代法的准确性.

3)本文提出的保形分析方法，不仅可以用于点阵式充气翼的保形分析，还可以应用到充气天线、飞艇囊体和高空气球等其他充气膜结构的三维保形分析中，具有良好的拓展潜力.

［1］毛丽娜.充气膜结构反射面的保形分析与优化方法研究［D］.哈尔滨:哈尔滨工业大学，2010.

［2］王鹏.ETFE气枕的力学分析及其蒙皮效应的研究［D］.哈尔滨:哈尔滨工业大学，2010.

［3］江锡虎，谢步瀛，陈慧进.充气膜结构非线性分析的ANSYS实现［J］.结构工程师，2006，22(1):38-42.

［4］赵 冉，魏德敏，孙文波，等.深圳宝安体育场屋盖索膜结构的找形和索的破断分析［J］.工程力学，2010，27(S1):274-277.

［5］朱丙虎，张其林，杨宗林.上海世博会世博轴索膜结构屋面有限元分析与研究［J］.土木建筑与环境工程，2011，33(1):100-103.

［6］向新岸，田伟，赵 阳，等.考虑膜面二维变形的改进非线性力密度法［J］.工程力学，2010，27(4):251-256.

［7］袁驷，刘学林，叶康生.张拉膜结构极小曲面找形的有限元线法求解［J］.土木工程学报，2010，43(11):1-7.

［8］STAVREV V.A shape grammar for space architecture-I.pressurized membranes［C］//Proceedings of 40th International Conference on Environmental Systems，Hotel Fira Palace.Barcelon，Spain:AIAA，2010，2010-6071:1-13.

［9］LEWIS W J，BREW J S，BRYANSTON-CROSS P，et al.Form-finding as a modelling tool for shaping mechanical components:A feasibility case study of an axial-flow compressor blade［J］.Engineering Structures，2011，33(9):2612-2620.

［10］TAKAHASHI D，LEBEAU R P.Computational investigation of flow over inflatable airfoils at multiple reynolds numbers［C］//Proceedings of 49th AIAA Aerospace Sciences Meeting.Orlando，Florida:AIAA，2011，2011-377:1-9.

［11］HAUSER T，JOHANSEN T A，LeBEAU R P.Computational optimization of a low reynolds number inflatable airfoil［C］//Proceedings of 20th AIAA Computational Fluid Dynamics Conference.Honolulu，Hawaii:AIAA，2011，2011-3534:1-9.

［12］ROWE J M，Suzanne Weaver Smith.Challenges of modeling inflatable wings［C］//Proceedings of 48th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics，andMaterialsConference.Honolulu，Hawaii:AIAA，2007，2007-1848:1-18.