双基固体推进剂的特性研究①

张建彬，鞠玉涛，周长省

(南京理工大学机械工程学院，南京 210094)

0 引言

由于双基固体推进剂燃温和燃速低、燃气清洁、强度高，目前在各类中小口径火箭、炮射火箭增程发动机及导弹燃气发生器上使用。双基推进剂的力学性能与复合推进剂的力学性能有明显的差异，具有高温强度低、低温延伸率低的特点。不少学者认为固体推进剂是粘弹性材料［1－3］，而也有学者认为固体推进剂为粘弹塑性材料［4－5］。在高于玻璃化温度时双基推进剂具有粘弹性材料的性质，其又属于线型高聚物材料［6］，所以可认为双基推进剂为粘弹塑性材料。国内在分析推进剂药柱结构完整性时的破坏判据，还是采用最大应变理论或最大应变能理论［7］，这对双基推进剂来说就不太合适。

本文在试验研究的基础上，基于数理统计理论对双基推进剂的力学性能进行了讨论分析，以期为双基推进剂药柱设计和结构完整性分析提供理论支持。

1 试验材料和设备

1.1 推进剂主要成分及试件

双基推进剂主要原料:硝化棉(NC，56%)、硝化甘油(NG，26.7%)、二硝基甲苯(DNT，11.3%)、其他(6%)。采用某双基推进剂药柱制取试验用试件，根据QJ 924—85将药柱采用机械加工方法制成哑铃状试件，长度单位为mm，如图1所示。

1.2 试验设备及试件的制备

为了消除机加工时的残余应力，需将试件在323.15 K下保温48 h。试验前，将试件和夹具在试验温度下保温4 h时。试验时，将试件及夹具装置于具有温控箱的QJ 211B型电子万能试验机上，同时在试件的标距内安装上纵向引伸计。试验温度分别为233.15、288.15、323.15 K，单轴拉伸应变率ε·分别为5.05 × 10－3、1.262 5 × 10－2、2.525 × 10－2、5.05 ×10－2、1.262 5 ×10－1s－1，每组试验重复 5 次。试验前检查计算机程序设置无问题时，启动计算机程序实时记录推进剂单向拉力和试件的变形值。

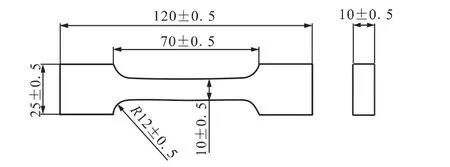
图1 双基推进剂试件Fig.1 Double-base propellant specimen

2 结果与分析

每种工况重复5次，试验后对应力-应变试验曲线进行平均处理，如图2所示。由图2可知，双基推进剂在不同条件下呈现不同的材料性质，低温(233.15 K)时处于玻璃态，近似为脆性材料，致使力学性能不太稳定，而常温(288.15 K)和高温(323.15K)时出现塑性流动现象，明显为粘弹塑性材料。

图2 不同温度和应变率下应力-应变曲线Fig.2 Stress-strain curves at different temperatures and strain rates

2.1 双基推进剂屈服点的定义

推进剂在低温下无屈服，而在常温和高温下双基推进剂存在塑性流动，但对于双基推进剂的屈服值还没有明确的定义。文献［8］认为，粘弹塑性材料在屈服前为粘弹性体，当到达屈服状态后为粘弹塑性体，粘弹性材料和粘弹塑性材料的性能有很大的差异。可见，对于粘弹塑性材料来说，屈服状态是重要的力学性能表征参量。文献［9］认为，高聚物存在负荷降时，屈服应力定义为拉伸负荷达到极大值时的真应力;不存在负荷降时，屈服应力定义为沿应力应变曲线的起始部分和最终部分作2条切线的交点所对应的应力值。显然，该方法所得屈服应力偏大，而屈服应变偏小。

针对双基推进剂的特殊性，本研究认为其屈服点为45°直线与应力-应变曲线相切的点，这样处理的优点是方便快捷且降低了误差。采用该方法以288.15 K时应变率为2.525 ×10－2s－1下的平均应力-应变曲线为例，确定屈服点的示意图，如图3所示。双基推进剂力学性能及依据这种方法确定不同条件下的屈服值，如表1～表3所示。

图3 确定屈服点的示意图Fig.3 Schematic diagram of determined yield point

表1 233.15 K下的力学性能Table 1 Mechanical properties under 233.15 K

表2 288.15 K下的力学性能Table 2 Mechanical properties under 288.15 K

表3 323.15 K下的力学性能Table 3 Mechanical properties under 323.15 K

2.2 双基推进剂力学性能与应变率的相关性

由一元回归结果易知，屈服应力σy、应变εy、断裂应力σb和延伸率εb与应变率对数lgε·呈线性关系，相关系数都接近于1，它们的一元线性回归曲线如图4所示。

图4 推进剂力学性能的回归曲线Fig.4 Regression curve about propellant mechanical properties

由表1～表3和图4可知，双基推进剂在常温和高温不同拉伸速率下屈服值的变化趋势基本一致。在同一温度下，随应变率增加，屈服强度和屈服应变随之增加，但这2种温度下的屈服应变差别不明显;在同一应变率下，随温度增加，屈服强度和屈服应变随之减小，但屈服应变在较低应变率时变化较小。而断裂强度和断裂延伸率的变化趋势不完全一致，随应变率增加，断裂强度随之增大，断裂延伸率在低温时近似为脆性材料随之减小，而在常温和高温时为粘弹塑性材料随之增大，但变化较平缓。可见，双基推进剂的力学性能与应变率和温度有明显的相关性。

由文献［10］中的t检验法结合试验数据可得回归效果，如表4所示。由表4可知，检验假设的结果都在拒绝域之内，可认为上面的一元回归效果是显著的。通过分析可见，本文所提出的屈服点确定方法满足应变率相关性且误差较小，说明这种确定方法的可信性较好。

2.3 强度准则的建立

严格地说，药柱破坏判据是一个很复杂的问题，涉及多向应力-应变状态、加载历史、应变速率、温度与湿度老化等多种因素。

通常情况下，在分析结构完整性问题时，破坏判据应视载荷类型而定:当受温度载荷和工作压强载荷时，以延伸率作为判据较为合理;而受加速度载荷和自重载荷时，以强度作为判据较为合理。这是因为受温度载荷和工作压强载荷时，发动机壳体很刚硬，且是发动机的主要承力部件，药柱只要随它变形而不至于产生裂纹与脱粘就能保持其完整性。所以，应以延伸率作为判据。而在加速度载荷和自重载荷作用下，推进剂药柱必须承载。所以，应以强度作为判据［11］。

为了安全起见，本文采用屈服值来确定双基推进剂的破坏强度准则，双基推进剂在常温或高温时到达断裂强度之前已有明显的塑性变形。所以，破坏情况不宜用断裂强度σb或最大延伸率εb来判断。

当受温度载荷和工作压强载荷时，对于多向应力状态，由于在使用范围内推进剂的韧性较好，采用八面体剪应变理论作为破坏判据较合理。对平面应变状态正八面体剪应变为

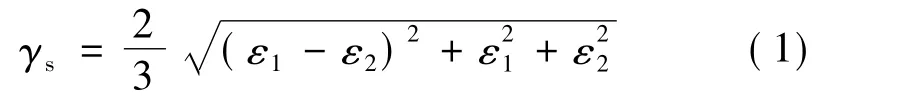
而其临界值γsm与屈服延伸率的关系为

式中 ν为推进剂材料的泊松比。

将计算结果代入式(1)，试验结果代入式(2)，分别计算出γs和γsm，便可对固体推进剂药柱做出安全评判:

当受加速度和自重载荷时，由图4可知，σy在常温和高温下与温度和应变率有明显的相关性。所以，破坏强度采用下限，则准则为

式中 N为安全系数，根据经验取1.2～2.8。

表4 t检验法的结果(取a=0.05)Table 4 Results of t test methods(a=0.05)

3 结论

(1)对双基固体推进剂试件进行了单轴拉伸试验，分析了应力-应变曲线的特征，低温(233.15 K)时处于玻璃态，近似为脆性材料，而常温(288.15 K)和高温(323.15 K)时出现塑性流动现象，明显为粘弹塑性材料。

(2)由于针对没有负荷降的粘弹塑性材料的屈服点还没有明确的定义，本文在前人的基础上，提出了一种针对双基推进剂屈服值的判断方法。

(3)用一元回归理论对双基推进剂的力学性能与应变率对数的关系进行了分析和假设检验。结果表明，它们的回归效果是显著的，且双基推进剂的力学性能与温度和应变率有明显的相关性。

(4)根据双基推进剂为粘弹塑性材料的特性，其到达断裂强度之前已有明显的塑性变形。为了安全起见，提出了针对双基推进剂的强度准则。

［1］Ren Ping，Hou Xiao，He Gao-rang，et al.Comparative research of tensile and compressive modulus of composite solid propellant for solid rocket motor［J］.Journal of Astronautics，2010，31(10):2354-2359.

［2］Deng Kai，Yang Jian-hong，Huang Wei-wei，et al.A new method to obtain shear modulus of solid propellant［J］.Acta Astronautica，2011，69(7-8):440-444.

［3］职世君，孙冰，张建伟.固体推进剂复合型裂纹扩展数值计算［J］.固体火箭技术，2011，34(1):28-31，47.

［4］Baris Kalaycioglu，Dirikolu M Husnu，Veli Elik.An elastoviscoplastic analysis of direct extrusion of a double base solid propellant［J］.Advances in Engineering Software，2010，41(9):1110-1114.

［5］邓凯，阳建红，陈飞，等.HTPB复合固体推进剂本构方程［J］.宇航学报，2010，31(7):1815-1818.

［6］李葆萱，王克秀.固体推进剂性能［M］.西安:西北工业大学出版社，1990.

［7］孟红磊，鞠玉涛，周长省，等.改性双基推进剂损伤破坏研究［J］.弹道学报，2011，23(2):79-81，86.

［8］杨挺青.粘弹塑性本构理论及其应用［J］.力学进展，1992，22(1):10-19.

［9］徐懋，漆宗能，译.固体高聚物的力学性能［M］.北京:科学出版社，1980.

［10］盛骤，谢式千，潘承毅.概率论与数理统计［M］.北京:高等教育出版社，2006.

［11］唐国金，周建平.自由装填药柱的结构完整性分析［J］.固体火箭技术，1994，17(2):13-19.