基于滑模反演控制方法的纵向制导控制一体化设计①

张金鹏，周池军，雷虎民

(1.北京航空航天大学自动化科学与电气工程学院，北京 100191;2.空军工程大学防空反导学院，西安 710051)

0 引言

传统制导控制系统设计方法假设制导回路和控制回路可以分离，控制回路设计不依赖于制导回路，这种方法在过去被证明是有效的，并且广泛应用。随着战术弹道导弹技术的不断成熟，目标机动性能的大幅度跃升对拦截弹的机动过载和快速响应能力提出了更高要求，传统的制导控制系统设计方法的弊端逐渐暴露，制导控制一体化设计在提高制导精度、减小拦截弹响应时间方面的独特优势使其在拦截高速机动目标方面具有广阔的应用前景［1］。制导控制一体化设计问题可归结为一类非匹配不确定系统的输出跟踪问题。反演控制具有对非匹配不确定性的抑制能力，将其与滑模控制结合，进行一体化控制器设计已成为当前制导控制一体化研究的热点。文献［2］将动态面设计思想融入基于滑模反演控制理论的一体化控制算法设计中，取得了较好的控制效果，但在设计过程中没有考虑执行机构速率的限制。文献［3－4］利用神经网络在线逼近系统的不确定性，基于滑模反演控制理论设计了一种一体化算法，通过调整参数来提高系统状态跟踪误差的收敛速度，但该算法较复杂，需要调整的参数较多。文献［5］以零控脱靶量为目标进行了滑模反演一体化算法设计，并利用干扰观测器对系统的不确定性进行了估计，但只采用单个特征点的气动数据进行仿真验证，缺乏足够的说服力。以上文献都针对系统的非匹配不确定性进行了基于滑模反演控制理论的一体化算法设计，虽然都达到了一定的效果，但是这些算法几乎都是用于攻击低速目标或者是地面固定目标，对于拦截高速机动目标的适用性还需要进一步检验。

本文针对拦截高速机动目标的末制导问题，设计了拦截弹纵向通道的滑模反演一体化控制算法。通过建立合理的一体化制导控制系统模型，将制导控制一体化设计问题转化为系统的输出跟踪问题，结合动态面设计思想，采用低通滤波器克服了反演控制本身存在的计算膨胀问题。该一体化算法不但能够保证拦截弹自身姿态的稳定，而且具有较高的制导精度。

1 问题描述

考虑滚转通道稳定的尾翼控制拦截弹的末端拦截问题，假设拦截过程中攻角和侧滑角很小，对于拦截弹的某一通道来说，其余通道对其产生的耦合影响是有界的［6］。基于以上假设，可将拦截弹制导控制系统分解为纵向通道和侧向通道2个独立的子系统，对每个子系统分别进行设计。由于纵向通道与侧向通道的制导控制一体化设计具有相似性，故只研究纵向通道的制导控制一体化设计，利用纵向通道与侧向通道的对偶性可以将所设计的算法简单地扩展到三维。

2 制导控制一体化算法设计

2.1 模型转换

为便于进行滑模反演控制算法设计，将上述一体化模型转换为相变量方程。令取则可以将上述模型转换为含有非匹配不确定性的线性模型:

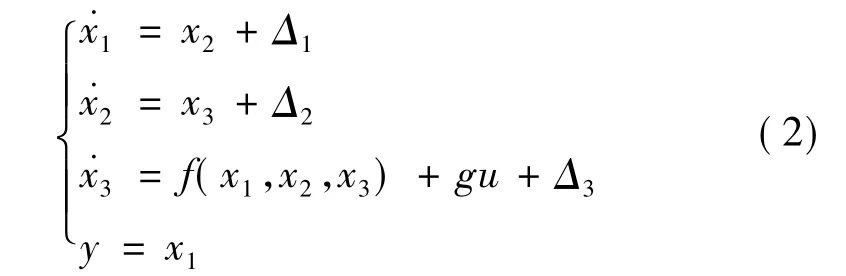
式中 x1、x2、x3为系统状态变量;u=δz为系统控制输入;g为控制输入项系数;y为系统输出;Δ1、Δ2、Δ3为系统的不确定性;f(x1，x2，x3)=h1x1+h2x2+h3x3为确定的线性函数;h1、h2、h3、g、Δ1、Δ2、Δ3的具体表达形式参考文献［7］。

在上一节建立制导控制一体化模型时，为降低模型转换的复杂度，将目标的机动加速度作为不确定性处理，但实际上目标加速度并不是完全未知的。如果视线角速度、弹目相对距离和相对速度等信息可以测量得到，那么结合导弹自身的运动信息能够近似估计目标的机动信息［8］。因此，可以将目标机动引起的不确定性从Δ1、Δ2、Δ3中分离出来，从而减轻控制器的设计负担，降低系统设计的保守性［4］。故可以将相变量方程(2)进一步转换为

其中:

2.2 一体化控制算法设计

一体化控制算法设计的目的是设计一个鲁棒状态反馈控制器，使得带有上述非匹配不确定性的线性时变系统的输出跟踪期望的输出轨迹，即视线角速度趋近于零，同时保证系统的其他状态有界。为了便于一体化控制算法设计，首先给出以下几点假设:

假设1:假设在参数摄动情况下，系统控制输入项系数始终满足g≠0。

假设3:假设μi(t)＞0，1≤i≤3为连续可导函数，且满足

定义闭环系统(3)的状态跟踪误差为

式中 α1、α2为第一步需要设计的虚拟控制律。

第一步:针对闭环系统(3)的前2个子系统，设计虚拟控制律 α1、α2的估计值 x2c、x3c为

其中，c1＞0，c2＞0，x2c、x3c可由 α1、α2滤波得到，一阶低通滤波器的动态方程为

式中 τ1、τ2为滤波器时间常数;α1、α2满足 α1(0)=x2c(0)，α2(0)=x3c(0)。

定义系统的估计误差为

对式(4)求导，并将式(5)、式(7)带入得

第二步:设计滑模控制律u，考虑闭环系统(3)的第三个子系统，对跟踪误差e3求导可得

取滑模面s=k1e1+k2e2+e3，选择系数k1、k2使多项式p2+k2p+k1满足Hurwitz稳定条件，对s求导可得

她在幼儿园的窗外，默默观察孩子在教室里面的活动。两个孩子都给了他，他以及他的家人极为喜爱两个混血孩子。她打算离开南半球，什么都没有要，只想离开5年僵滞停顿的生活环境。无法跟孩子在一起。也许也可以像贞谅，带着孩子在世间东奔西颠，但她不觉得这是好的方式。这个家庭式幼儿园提倡美德、素食、劳动、安静，把孩子托付给一个小范围的有规范的社会是必要的。他们在那里受到理念的约束和指导，周围都是同类，不会觉得隔离和边缘。

设计滑模控制律:

其中:

式中 uc为补偿项;uvss为切换控制项;K为控制增益;

2.3 稳定性分析

为便于分析稳定性，首先给出如下引理［7，9－10］:

引理1:设K∶D→R是定义域为D⊂Rn且包含原点的连续正定函数，并假设对于某个r＞0有Br⊂D，则对于所有x∈Br，存在定义在［0，r］上的κ类函数a1和a2，满足:

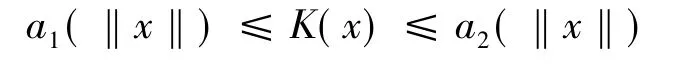
如果D=Rn且K(x)是径向无界的，则存在κ∞类函数a1和a2在［0，∞)上有定义，使得上式对于任意x∈Rn都成立。

引理2:假设对于所有 μi(t)＞0，1≤i≤3，则以下不等式恒成立:

引理3:对于系统:

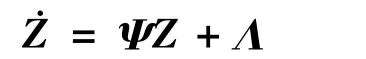
(1)若存在正常数m1使得‖Λ‖≤m1，则存在正常数m2使得‖Z‖≤m2;

(2)若Λ渐近收敛到零，则Z渐进收敛到零。

定义闭环系统(3)的Lyapunov函数为

对V求导可得

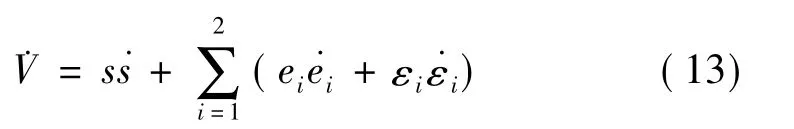
由估计误差可得

由引理1可知，存在κ∞类函数κ2和κ3使得

将式(10)、式(14)～式(17)带入式(13)，根据假 设2、假设3及引理2可得

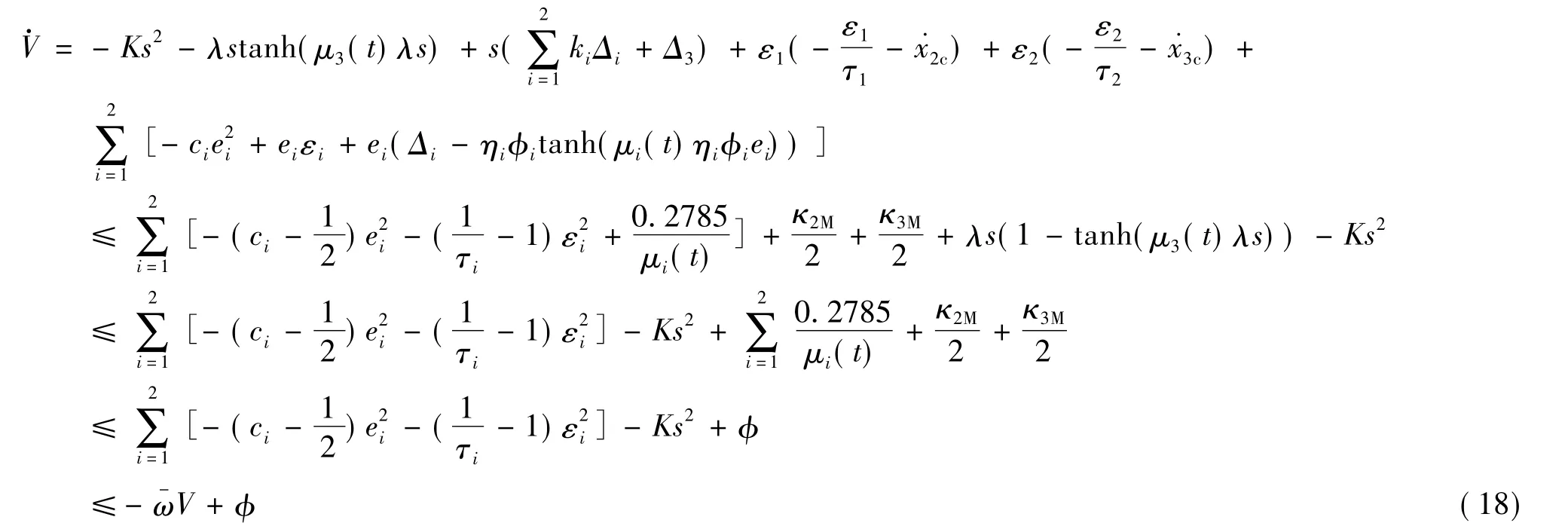
根据引理3可知，闭环系统的所有状态均有界。通过选择适当的控制器参数，可保证闭环系统输出跟踪误差在有限时间收敛到原点附近一个任意小的邻域内，而且此邻域的大小与不确定性的界限无关，仅由控制器参数决定［11］。

3 仿真验证

3.1 仿真结果

假设拦截弹的初始位置为(1 000 m，18 000 m)，速度为1 600 m/s，初始弹道倾角为15°，初始攻角0°，俯仰角速度初值为0(°)/s。初始弹目视线角为30°，目标距离拦截弹15 000 m，速度为2 000 m/s，初始弹道倾角为220°，机动过载为5gsinπt。

当弹目相对距离小于200 m时，进入导引头盲区，制导控制系统不再进行指令计算，舵面保持停控时刻的偏转角度不变，拦截弹依靠自身惯性飞向目标。假设拦截过程中拦截弹受到以下物理条件约束:

控制算法中的有关参数选择如下:滤波器时间常数 τ1= τ2=0.01 s，仿真步长取 0.001 s，c1=3，c2=3，k1=5，k2=3，K=5。

为了验证本文所设计的一体化算法(IGC)的有效性，将其与传统的制导控制系统分开设计方法进行比较。传统设计方法引用文献［4］中采用的变结构制导+滑模控制设计方法(VSG-SMC)，具体仿真结果如图1～图6所示。

为了检验本文所设计的一体化算法的鲁棒性和制导效果，在其他仿真条件不变的情况下改变气动参数摄动量和目标的机动方式，并在视线角速度量测信号中加入信号本身大小2%的零均值高斯白噪声，进行200次蒙特卡洛仿真，得到拦截参数如表1所示。

图1 弹目相对运动轨迹Fig.1 Trajectories of interceptor and target

图2 状态跟踪误差变化曲线Fig.2 Curves of state track error

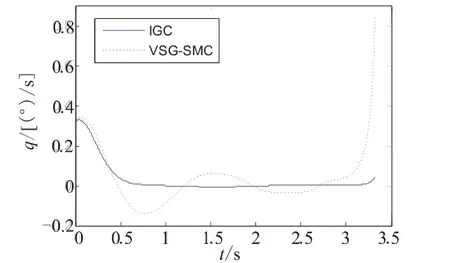
图3 视线角速度变化曲线Fig.3 Curves of line of sight rate

3.2 结果分析

由图1可知，采用本文所设计的一体化算法得到的拦截弹弹道曲线比较平直，表明拦截弹受到的机动过载更小。

由图2～图3可知，采用一体化算法时，系统的状态跟踪误差e2、e3和视线角速度均能够迅速收敛到零，体现了一体化算法的有效性。虽然由于目标机动产生的干扰随着弹目距离的减小而逐渐增大，使系统的不确定性增大，导致停控时刻状态跟踪误差e2、e3和视线角速度出现了小幅发散，但是对于终端脱靶量影响不大。而采用传统设计方法时，视线角速度对于目标作正弦机动比较敏感，而且在停控时刻视线角速度发散较为明显，从而增大了终端脱靶量。

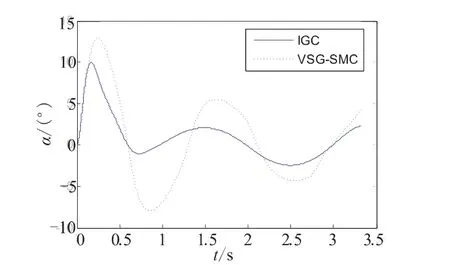
图4 攻角变化曲线Fig.4 Curves of angle of attack

图5 俯仰角速度变化曲线Fig.5 Curves of pitch rate

图6 舵偏角变化曲线Fig.6 Curves of rudder deflection angle

由图4～图6可知，2种设计方法得到攻角、俯仰角速度和舵偏角均未超出物理条件限制，拦截弹能够保证自身姿态的稳定，当系统的状态处于趋近运动阶段时，采用传统设计方法得到的攻角和舵偏角较大，当系统的状态处于滑模运动阶段时，为了使系统的状态维持在滑模面上，采用传统设计方法需要产生较大的舵偏角、攻角和俯仰角速度来消除目标机动引起的干扰，而采用一体化算法得到的拦截弹舵偏角变化更加平稳，舵面偏转角度较小，克服了滑模控制引起的抖振问题，大大降低了对舵机的要求。

由表1可知，在目标不机动、正弦机动和圆弧机动3种情况下，制导控制一体化算法对于气动参数的摄动均具有较强的鲁棒性。与传统的制导控制系统分开设计方法相比，一体化设计能够在更短的时间内以更高的制导精度拦截目标。一体化设计方法相对传统设计方法在拦截高速机动目标方面具有明显的优势。

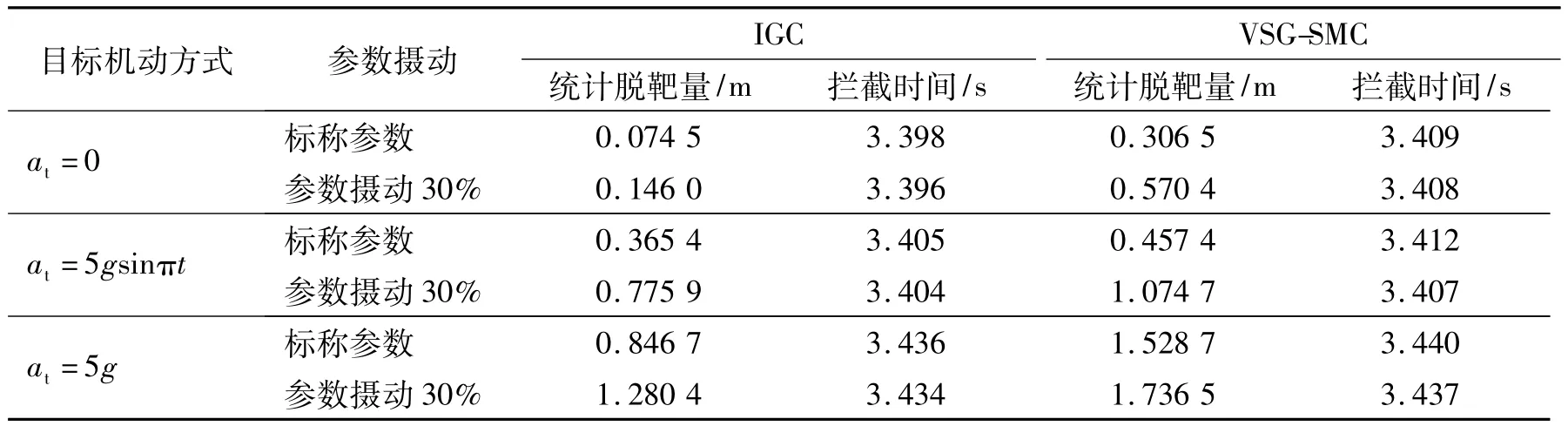
表1 拦截参数对比Table 1 Comparison of interception parameters

4 结论

(1)对于高速机动目标的拦截问题，制导控制一体化设计仍然具有较强的适用性。

(2)与传统的制导控制系统分开设计相比，制导控制一体化设计具有更短的拦截时间和更高的制导精度。

(3)所设计的一体化算法能够保证拦截弹自身状态的稳定，并且对于参数摄动具有较强的鲁棒性。

［1］Nathan Harl，Balakrishnan S N，Craig Phillips.Sliding mode integrated missile guidance and control［C］//AIAA Guidance，Navigation，and Control Conference.Toronto，Ontario Canada，2010-7741-7759.

［2］Hou Ming-zhe，Duan Guang-ren.Adaptive dynamic surface control for integrated missile guidance and autopilot［J］.International Journal of Automation and Computing，2011，8(1):122-127.

［3］Manu Sharma，Nathan D Richards.Adaptive，integrated guidance and control for missile interceptors［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit.2004，Providence，Rhode Island.

［4］张保群.导弹俯仰通道制导控制一体化设计［D］.哈尔滨工业大学，2008.

［5］Tae-Won Hwang，Min-Jea Tahk.Integrated backstepping design of missile guidance and control with robust disturbance observer［C］//SICE-ICASE International Joint Conference.2006，Busan，Korea.

［6］侯明哲.寻的导弹导引控制一体化设计［D］.哈尔滨工业大学，2011.

［7］段广仁，侯明哲，谭峰.基于滑模方法的自适应一体化导引与控制律设计［J］.兵工学报，2010，31(2):191-198.

［8］Alex Zhurbal，Moshe Idan.Effect of estimation on the performance of an integrated missile guidance and control system［J］.IEEE Transaction on Aerospace and Electronic Systems，2011，47(4):2690-2708.

［9］Plycarpou M M，Ioannou P A.A robust adaptive nonlinear control design［J］.Automatica，1995，31:423-427.

［10］王坚浩，胡剑波.一类非匹配不确定非线性系统的鲁棒跟踪控制［J］.控制与决策，2011，26(5):727-731.

［11］Van Oort E R，Sonneveldt L，Chu Q P，et al.Modular adaptive input-to-state stable backstepping of a nonlinear missile Model［C］//AIAA Guidance，Navigation and Control Conference and Exhibit.2007，Hilton Head，South Carolina.