微型固体推力器瞬态工作过程数值模拟①

李 腾，方蜀州，刘旭辉，马红鹏，汤 旭，赵 婷

(1.北京理工大学宇航学院，北京 100081;2.中国空间技术研究院北京控制工程研究所，北京 100190)

0 引言

基于MEMS技术制造的固体微推力器具有结构简单、功耗低、无可动部件及其带来的摩擦损失小、可靠性高等诸多优势。固体微推力器最大的优势是集成度高，可集成在一块基片上组成阵列。目前，阵列式推进系统已在动能拦截器等方面投入应用，如美国的增程拦截弹ERINT-1。基于上述特点，固体微推力器成为微推进系统方面新的研究热点。

目前，对固体微推力器工作特性的研究主要集中在其微尺度喷管上，国内外学者对微尺度下喷管内粘性和热损失效应，稀薄效应对喷管内流场的影响、微喷管内两相流方面的研究开展了较多的工作［1－6］，但对推力器燃烧室-喷管一体化结构的推力器非稳态工作过程研究相对较少。2011年，西班牙国家宇航中心的José A Morínigo等对其设计的一种新型固体微推力器结构在近真空环境下进行了非稳态一体化仿真。结果表明，这种结构可很好地减小热损失，二阶滑移边界条件对推力幅值有45%的影响［7］。目前，对固体微推力器非稳态工作情况的研究仍多以实验手段为主，但微型推力器工作过程时间通常较短(不到2 s)，且尺寸为亚毫米级，体积微小，测试难度大，难以直接获得内流场各物理量数据。因此，通过数值模拟手段对推力器一体化模型及其瞬态工作过程的研究是有必要的。

由于药柱成型及装填难度的限制，当前国内外的固体微推力器多采用端燃装药，由靠近推进剂表面的点火电阻点燃推进剂。其中，以法国国家科学研究中心(LAAS-CNRS)开展的相关研究最具有代表性，本文主要基于LAAS-CNRS的平板结构推力器模型进行初步研究。

1 物理模型

1.1 推力器几何模型

推力器蚀刻深度545 μm，燃烧室宽度1 500 μm，长度5 300 μm，喷管入口宽度与燃烧室宽度相等，喉部宽度为150 μm，出口宽度为600 μm，燃烧室壁厚625 μm，扩张半角 10°［8］，假定推力器壁面完全光滑。

本文研究的推力器蚀刻深度大于喉部宽度的3倍，因此可忽略三维壁面效应［9］。同时，出于简化分析和计算成本的考虑，设置推力器在蚀刻方向上的壁面为绝热壁面，采用二维CFD模型进行分析。微型固体推力器几何模型如图1所示。

图1 微型固体推力器几何模型Fig.1 Geometric model of solid propellant micro-thruster

1.2 控制方程

1.2.1 流场区域控制方程

对微尺度下的流场，克努森数(Kn)是决定气体流动状态的关键无量纲参数，其定义为分子平均自由程(λ)与特征几何长度(L)的比值，可表示为当地雷诺数(Re＇)、气体比热容比γ和当地马赫数(Ma)的函数，其表示方式如下:

对于Kn＜0.14的微尺度流动，一阶速度滑移和温度突跃边界条件能准确模拟微尺度效应对流场的影响，表示如下［10］:

考虑热蠕变的一阶速度滑移边界条件:

壁面温度突跃:

式中 ug和Tg分别为紧邻壁面处流体沿壁面的切向速度和温度;uw和Tw分别为壁面移动速度(本文中壁面静止，uw=0)和温度;σv为壁面动量调节系数;σT为热调节系数。

对本文的情况，温度突跃对流场的影响可以忽略［11］。因此，只考虑一阶速度滑移，按完全漫反射模型取σv=1。

主流区控制方程仍然为通用N-S方程:

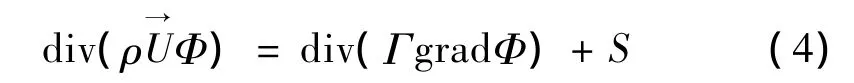
该通用方程包含了连续方程、动量方程和能量方程。

燃气满足理想气体状态方程:

燃气粘度采用Sutherland方程描述:

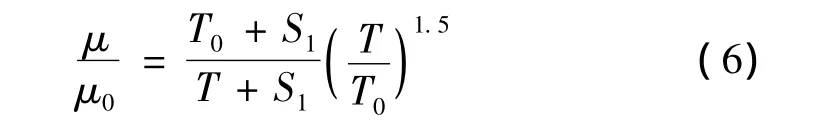
式中 μ0为参考温度T0=273.11 K时的动力粘度，在此对应的值为1.663×10－5kg/(m·s);S1为常数，其值为106.67 K。

微尺度下的层流到非充分发展湍流的转捩雷诺数与常规尺度下表现出一定的差异，会发生转捩提前的现象。根据国内外微流动元器件的部分实验结果，可近似以式(7)概括［12］:

式中 L为流动方向上的长度;Dh为水力直径。对本文的模型，推力器的，即 Recr＜446.7。

作为初步计算，本文采用标准k-ε模型进行流场仿真。求解器为隐式耦合非稳态求解器，计算方法采用SIMPLE算法。

首先，对不考虑微尺度效应的推力器流场进行计算，得到克努森数分布后，再考虑是否对壁面添加滑移边界条件。

1.2.2 固体区域控制方程

对固体区域仅考虑热传导，其控制方程为二维常物性、无内热源、非稳态的导热微分方程:

1.3 物性参数

推进剂采用平台双基推进剂SD，其主要参数如表1所示［13］。其中，燃速采用添加了少量黑火药后的推进剂在常压环境下于微推力器内通过实验完全燃烧后获得的平均燃速［8］。药柱参数参考同类推进剂相关参数，如表2所示。

壁面分别设置为文献［8］中组成推力器壳体的2种材料进行计算。由表3结合热扩散率的定义式计算得到二者的热扩散率分别为 8.6572 ×10－5、7.33 ×10－7m2/s。

表1 推进剂参数Table 1 Parameters of the propellant

表2 药柱参数Table 2 Parameters of the grain

表3 壁面材料参数Table 3 Parameters of the wall

1.4 计算区域、网格划分及边界条件

本文考虑的计算模型区域和推力器区域如图2所示。计算网格采用结构网格，图3为计算网格(局部)。

图2 计算区域Fig.2 Computational area

图3 局部计算网格(推力器喷管及附近区域)Fig.3 Partial computational mesh(nozzle and the area nearby)

模型出口条件设定为压力出口，压强为101 325 Pa，计算域初始温度为300 K。燃烧室外壁面设为绝热壁面，根据第三类边界条件:

设置燃烧室、喷管内壁面及推进剂表面为热耦合壁面。

假定推进剂在燃烧表面完全燃烧，因此将燃气作为单一气体组分考虑，对推进剂表面相邻流场区域单元通过FLUENT用户自定义函数UDF加载燃气质量源项、动量源项与能量源项。其公式表示如下:

式中 r为推进剂燃速;A为推进剂燃面面积;ρg为燃气密度;cp为燃气比定压热容;Tf为燃温。

燃面退移过程通过动网格进行模拟，假定燃面按实测平均燃速4.6 mm/s平行退移，网格更新方法为动态分层法。时间步长为0.001 s，为保证计算准确性，内迭代步数为1 000。

本文推力的计算采用将壁面压力对面积积分，再与粘性阻力矢量求和，最后取轴向分量的方法获得。

2 计算结果

2.1 流动微尺度效应

首先，不考虑滑移边界条件对微推力器工作过程进行计算，得到推力器内部基于喉部雷诺数的克努森数分布，推力器壁面材料选择Macor Corning Ceramic。图4为0.2 s和1.0 s时推力器内流场克努森数分布情况。

图4 0.2 s和1.0 s时刻推力器内流场努森数分布Fig.4 Kudsen number distribution inside the thruster at 0.2 s and 1.0 s

可看出，推力器喷管内部喷喉处克努森数最大，这与文献［14］计算得到的喷管克努森数分布有所不同。其原因在于本文计算的推力器喷喉处流速未达到声速，喷喉未处于壅塞状态，喷管扩张段压力沿流动方向升高导致克努森数下降。根据克努森数云图，喷管内克努森数均大于0.001，应对喷管内部流场考虑速度滑移边界条件［11］。

图5为0.1～1 s间喷喉处壁面和喷管出口处壁面滑移速度随时间的变化规律。可看到，喷喉壁面处的速度滑移现象较为明显，其值分布于23～28 m/s之间;而喷管出口处速度滑移现象不明显，其值分布于2～4 m/s之间。这与喷管内克努森数的分布情况是相一致的，即克努森数越大，稀薄效应越强，壁面滑移速度越大。从图6所示的推力-时间曲线可看出，对本文的推力器及其工作条件，滑移边界条件对推力的影响很小，对平衡段推力最大只有1.5%的差异，这与Ivanov等的结论相一致［2］。因此，在下面计算中忽略滑移边界条件。

图5 0.1～1 s间喷喉和喷管出口壁面滑移速度-时间曲线Fig.5 Wall slip velocity-time curves for nozzle throat and nozzle outlet between 0.1 s and 1s

图6 考虑一阶速度滑移边界条件和无滑移边界条件后的推力-时间曲线Fig.6 Thrust-time curves with and without 1st order velocity slip boundary condition

2.2 推力器瞬态温度场

忽略流动微尺度效应后分别对壁面材料为Macor Corning Ceramic和Si的推力器进行非稳态仿真。

根据图7、图8可定性地看出，推进剂表面出现了一定的温度梯度，喷管内流场区域温度变化很小。采用Macor Corning Ceramic材料的推力器喷喉壁面附近存在明显的高温区。随着燃烧过程的进行，高温区逐渐沿轴向、径向扩散，造成喷管收敛段和扩张段壁面的温度也有所上升;而采用Si材料的推力器喷喉壁面及附近区域温升不明显。

根据式(9)，在初始时刻，对于喷管壁面，2种材料推力器的壁面边界层换热量相差较小，而Si的热导率远大于Macor Corning Ceramic的热导率，因而Si壁面的表面温度梯度较小。同时，Si的热扩散率远大于Macor Corning Ceramic的热扩散率，固体区域内部温度趋于一致的能力较强，这是导致上述现象的主要原因。

图7 采用Macor Corning Ceramic材料的推力器内部温度云图Fig.7 Temprature profile for thruster with Macor Corning Ceramic material

图8 采用Si材料的推力器内部温度云图Fig.8 Temprature profile for thruster with silicon material

在图9中，上述壁面温度分布曲线都有2个峰值，横坐标较小处的峰值表示与推进剂燃面接触的壁面温度，横坐标较大处的峰值表示喷喉处壁面温度。两峰值间的拐点表示喷管入口处壁面温度。

图9 不同时刻推力器内壁面温度分布曲线Fig.9 Temperature distribution curves at different moments

由图9可见，对于壁面采用Macor Corning Ceramic材料的推力器，喷管内壁面升温很快，在0.05 s内温度就由300 K上升至约1 000 K。随后，升温趋势随时间减小，最后温度趋于稳定。燃烧室内温度起初在燃面与喷管入口间存在较大的轴向梯度，随着燃烧的进行，壁面被不断加热，温度曲线趋于平缓。而对于壁面采用Si材料的推力器，喷管壁面升温较慢，高温区不明显。由于其较大的热扩散率，推进剂燃面位置之前的壁面温度也有所上升。

2.3 流动损失

在推进剂稳定燃烧的情况下，固体微推力器的推力损失主要由壁面热损失和粘性损失构成。图10为2种壁面材料推力器的推力-时间曲线。

图10 2种不同壁面材料推力器的推力-时间曲线Fig.10 Thrust-time curves for thrusters with different wall material

由图10可见，采用Macor Corning Ceramic材料的推力器能够维持推力上升至平衡段，而采用Si材料的推力器无法维持推力上升。

2.3.1 热损失

推力器内的总体热损失由通过燃烧室壁面的热损失和通过喷管壁面的热损失组成。图11为2种不同壁面材料推力器的热损失-时间曲线。可见，在数值上，采用Macor Corning Ceramic材料的推力器热损失明显小于采用Si材料的推力器热损失。同时，可看到采用Macor Corning Ceramic材料和采用Si材料的推力器，其热损失随时间的变化趋势具有一定共性:通过喷管壁面的热损失在工作过程中主要表现为下降趋势，而通过燃烧室壁面的热损失在工作过程中主要表现为上升趋势。结合上节的温度场分析，可认为其原因在于:流体到固体壁面的换热主要在表面边界层中进行，喷喉处粘性边界层较薄，表面温度梯度相对较大，流速最快，单位面积换热最剧烈，因而喷喉附近壁面温度上升较快。随着表面温度的上升，流场与壁面间温度梯度下降，因而通过喷管壁面的热损失表现为下降趋势。而随着推进剂燃面的不断退移，更多的推力器内壁面暴露于燃气环境中，且由图9可看出，燃烧室表面温度上升缓慢。因此，通过燃烧室壁面的热损失不断上升。

图11 2种不同壁面材料推力器的热损失-时间曲线Fig.11 Heat loss-time curves for thrusters with different wall materials

但是，采用2种不同壁面材料的固体推力器内的总体热损失却表现出相反的变化趋势:采用Macor Corning Ceramic材料的推力器总体热损失在下降了约0.25 s后趋于稳定，降幅约为25%;采用Si材料的推力器总体热损失却一直上升，增幅约为20%。这说明前者喷管壁面热损失的下降大于燃烧室壁面热损失的升高，而后者喷管壁面热损失的下降小于燃烧室壁面热损失的升高。二者总体热损失的变化趋势恰好与二者的推力曲线变化趋势相反。

2.3.2 粘性损失

通常由粘性阻力的变化趋势衡量粘性损失的变化趋势。图12为2种材料推力器的粘性阻力-时间曲线。由图12可知，壁面采用Si材料的微推力器喷管壁面粘性阻力数值相对较小，根据文献［5］，传热壁面的粘性阻力小于绝热壁面，结合图11热损失的计算结果，发现Si壁面热损失较大，粘性阻力较小;Macor Corning Ceramic壁面热损失较小，粘性阻力较大。可进一步认为:粘性阻力幅值与壁面热损失呈负相关性。

图12 2种不同壁面材料推力器的粘性阻力-时间曲线Fig.12 Viscous force-time curves for thrusters with different wall materials

喷管壁面粘性阻力首先经历短暂的上升，其主要原因是喷管内部速度场和温度场的建立;随后，在剩余工作时间内粘性阻力处于缓慢下降阶段，其主要原因是流场稳定后燃气往壁面的传热。

燃烧室壁面粘性阻力缓慢上升，这主要是由于燃面退移造成更大面积的壁面暴露于燃气流场中所导致的，但由于燃烧室内燃气流速较低，因此其幅值不大。可看到，总体粘性阻力的变化趋势主要由喷管壁面粘性阻力的变化趋势决定。

2.3.3 流动损失综合分析

总结粘性损失、热损失和推力的变化趋势。可得出:对本文研究的推力器，在推进剂按实测燃速稳定燃烧的前提下，推力随时间变化趋势的主要影响因素是总体热损失随时间的变化趋势，即推力器喷管壁面的热损失与燃烧室壁面热损失之和。对Macor Corning Ceramic材料，由于其热扩散率小，壁面附近升温明显，有效降低了与燃气间的温度梯度，减小了喷管壁面热损失，其降幅超过了燃烧室壁面热损失的上升幅值，使推力可上升并趋于稳定。对Si材料，由于其热扩散率大，壁面附近升温缓慢，喷管壁面热损失的下降无法抵消燃烧室壁面热损失的上升，造成推力持续下降，无法维持。壁面采用Macor Corning Ceramic材料不仅从数值上减小了壁面热损失，而且使壁面热损失随时间减小，抵消了燃烧室壁面热损失的上升，推力可上升并维持。文献［15］中的推力器实验结果表明:在提高壁面等效热导率前，推力器工作过程无法维持，而提高壁面等效热导率后，推力可上升至平衡段，这与本文的计算结果是相似的。

可看到，微型固体推力器的瞬态流动损失是一个复杂的过程，其影响因素主要有壁面材料、燃气温度、粘性和推进剂燃烧模型。本文作为初步研究，假定推进剂完全燃烧，忽略了推进剂配方改变导致的燃烧模型变化以及辐射传热等因素，该问题仍有待进一步研究。

3 结论

(1)通过所建立的端燃装药固体微推力器瞬态工作过程的流固耦合仿真模型，实现了对推力器内流场、壁面及推进剂内部温度场的一体化仿真。

(2)对本文所涉及的工作条件，推力器喷管内部克努森数虽然使喷喉壁面流场出现较明显的滑移现象，但喷喉处未达到壅塞状态，扩张段内压力升高，使得扩张段内克努森数降低。因此，扩张段内滑移现象不明显，对推力的影响很小，可忽略不计。

(3)采用Si材料的壁面热导率较高，因而在相近的初始传热量下壁面温度梯度低，且其热扩散率高，导致与燃气接触的喷管壁面升温缓慢，温度梯度减小缓慢。而采用Macor Corning Ceramic材料的壁面热导率较低，因而在相近的初始传热量下壁面温度梯度高，且其热扩散率较低，导致壁面附近区域温度升高较快，有效降低了温度梯度。

(4)粘性阻力的幅值与壁面散热量呈负相关性，总体粘性阻力的变化趋势由喷管壁面粘性阻力变化趋势主导。

(5)对本文研究的固体微推力器，在推进剂按实测燃速稳定燃烧的前提下，影响推力随时间变化趋势的主要因素是壁面热损失随时间的变化趋势，推力能否上升并维持的关键在于喷管壁面热损失的减小能否抵消由于燃面退移造成的燃烧室壁面热损失的增大。

［1］Markelov G N，Ivanov M S.Numerical study of 2D/3D micronozzle flows［C］//Proceedings of 22nd Symposium on Rarefied Gas Dynamics.2001.

［2］Ivanov M S，Markelov G N，Ketsdever A D，et al.Numerical study of cold gas micronozzle flow ［C］//37th Aerospace Sciences Meeting and Exhibit.1999.

［3］Alexeenko A A，Levin D A.Numerical simulation of hightemperature gas flows in a millimeter-scale thruster［J］.Journal of Thermophysics and Heat Transfer，2002，16(1).

［4］张斌，毛根旺，胡松启，等.固体微推力器气粒两相羽流场的数值模拟［J］.固体火箭技术，2011，34(3).

［5］吴素丽，胡松启，张斌，等.MEMS-SPMT喷管内的粘性和热损失研究［J］.固体火箭技术，2012，35(1).

［6］夏广庆，张斌，孙得川，等.微型固体姿控发动机微喷管内气粒两相流动规律的CFD-DSMC研究［J］.固体火箭技术，2012，35(3).

［8］Chaalane A，Rossi C，Esteve D.The formulation and testing of new solid propellant mixture(DB+x%BP)for a new MEMS-based microthruster［J］.Sensors and Actuators，A 138(2007).

［9］杨海威，朱卫兵，赵阳.拉伐尔型微喷管流场的三维模拟［J］.半导体技术，2009，34(10).

［10］Von Smoluchowski M.Ueber Würmeleitung in verdunnten gasen［J］.Annalen der Physik und Chemie 1898，64.

［11］Zhang Genxuan，Liu Minghou，Zhang Xianfeng，et al.Continuum based slip model and its validity for micro-channel flows［J］.Chinese Science Bulletin，2006，51(9).

［12］计光华，计洪苗.微流动及其元器件［M］.北京:高等教育出版社，2009.

［13］Gilles Fonblanc，Bruno Herran.A new insensitive，non-toxic double base propellant for rocket motors［C］//30th AIAA/ASME/SAE/ASEE Joint Propulsion Conference.2004.

［14］孙建威，刘明侯，张根烜，等.滑移边界条件对二维微喷管数值模拟结果的影响［J］.宇航学报，2005，26(6).

［15］Rossi C，Benoit Larangot，Denis Lagrange，et al.Final characterizations of MEMS-based pyrotechnical microthrusters［J］.Sensors and Actuators，2005，A 121.

［16］Kaili Zhang，Chou S K，Simon S Ang.MEMS-based solid propellant microthruster design，simulation，fabrication，and testing［J］.Journal of Microelectro-Mechanical Systems，2004，13(2).