RLV离轨制动耗尽关机制导方法研究①
2013-08-31张洪波汤国建
邹 毅,张洪波,汤国建,王 涛
(国防科技大学航天科学与工程学院,长沙 410073)
0 引言
离轨制动是在轨航天器在推力作用下的减速飞行过程,在制动发动机关机后,航天器可自由飞行至再入接口并获得预定的再入接口条件[1-2]。离轨制动问题普遍存在于行星探测器、飞船、航天飞机等多种航天器的返回任务中,与之相关的轨道优化、制导与控制技术是空天飞行器的关键技术。在欧空局的IXV计划中,离轨制动返回技术是一项重要的验证内容[3]。
离轨制动问题的早期研究以冲量式制动为主,将再入速度倾角Θe与地心距re看作再入接口条件,得出冲量Δv与推力角α的关系。在此基础上,求解最优离轨问题[4-5]。文献[6]采用这种方法,对升力式再入飞行器的离轨制动问题进行了研究。实际上,制动发动机推力是有限的,冲量假设与实际情况偏差较大。近年来,有学者提出“自主式离轨制导”的概念,通过推导有推力作用弧段的解析解,用快速多重打靶法来实现有限推力离轨制导[2,7],但这种方法仍过于繁琐,且无法用于固体火箭发动机的耗尽关机制导。
固体火箭发动机由于具有比冲大、发射准备时间短、维护检修容易等优点,而被广泛用于各类航天器,在实际应用时,需要解决燃料耗尽关机问题。采用速度增益制导时,为了实现耗尽关机,通常将离轨制动过程分成能量耗散段和闭路导引控制段。在能量管理模型中,以总视速度模量的一定比例来对二者进行划分;速度增益为零后,通过小幅修正需要速度倾角值来实现耗尽关机,这种方法较好地解决了以射程为主要性能指标的固体导弹耗尽关机制导问题[8];文献[9]提出以增益速度匹配固体推进剂耗尽时产生的可能速度增量,并直至发动机自然耗尽的末速匹配修正方案;文献[10]研究了再入点位置和再入角固定条件下的有限推力制导与耗尽关机问题,但未考虑推力的偏差。
本文针对可重复使用飞行器(RLV)离轨再入耗尽关机制导的总体设计需求,将离轨制动飞行分为2段,即能量耗散段和闭路制导段。通过推导飞行器能量与动量矩的变化特性,从理论上探讨了在燃料随机耗尽的情况下,推力方向对再入点参数的影响。仿真分析表明,该制导方法能在随机剩余燃料较多的情况下满足再入接口条件,这对在轨飞行器的多任务目标离轨再入、实现空间快速响应具有一定意义。
1 离轨制动有限推力制导策略分析
1.1 离轨再入问题建模
如图1所示,飞行器离轨再入返回轨道按照受力的不同可分为离轨制动段(OO1),自由飞行段(O1O2)和再入段(从O2点到地面)共3个阶段。其中,依靠制动发动机提供推力,由近地轨道进行制动变轨的阶段称为离轨制动段。

图1 有限推力离轨轨迹示意图Fig.1 Diagram of finite thrust deorbit trajectory
可重复使用飞行器通常设计为升力式再入飞行器,其在大气层内的横向机动能力很强,不需要通过改变轨道面来获得所需的横程。因此,在离轨制动过程中,只考虑平面内的运动问题。再入接口条件是为了保证飞行器顺利再入返回,而在再入接口处设定的约束条件,将再入接口取为大气边界环面在轨道平面内的投影,可用地心距为rf的圆来表示。离轨点与离轨时间通常由地面规划中心给定,再入点速度与速度倾角是关键的设计值。因此,再入接口条件可表示为:当r=rf时,vf∈[vemin,vemax],Θf∈[Θemin,Θemax]。
飞行器在地心惯性系中的共面离轨运动方程:

式中 v为速度;Θ为当地速度倾角;r为地心距;θ为航程角;m为质量;t为时间;F为发动机推力;α为攻角;μ为地球引力常数;Ve为发动机有效排气速度。
1.2 有限推力制动制导方法
如图2所示,离轨制导任务可描述为:已知离轨制动段任一t时刻的位置矢量与速度矢量分别为和v→(t),目标为轨道平面内地心距为rf的一维流形;在有限推力条件下,要求航天器在到达该流形时速度大小为vf,当地速度倾角大小为Θf,对到达时间不作要求。该问题与通常的交会、拦截问题都不一样,可看作一个广义拦截问题,通过速度增益制导方法进行导引。

图2 速度增益制导方法示意图Fig.2 Diagram of velocity gain guidance method

由式(2)、式(3)可求得vd和φa,根据准最优导引律的定义,φa实际上为推力方向与速度的夹角,若假定推力方向与飞行器的体轴重合,则对于平面内变轨问题φa即为攻角α。通过制导计算,实时改变推力方向,使得|vd|不断减小,直到|vd|<ε时(ε为指定精度),制导结束。
2 耗尽关机制导模型
2.1 闭路制导模型
本文提出一种基于连续推力作用下“动量矩-能量”变化特性的随机能量耗散模型,该模型主要是用于|vd|<ε后,通过控制攻角方向,使得再入点的速度与速度倾角在预定范围之内。
离轨轨道上任一点的能量与动量矩:

对式(4)和式(5)分别求导,并结合式(1)可得

由式(6)、式(7)可得
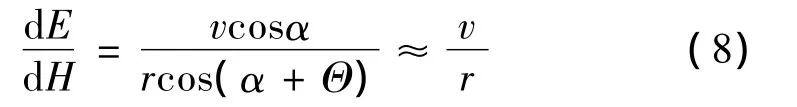
即当cosα≠0且cos(α+Θ)≠0时,飞行器的能量E与动量矩H的相对变化只与速度v和地心距r有关系,不可控;而将推力方向取为时时考虑到自由飞行段的动量矩守恒、能量守恒,而再入接口条件对应了E和H的取值范围,则可通过控制随机剩余燃料消耗阶段的E和H来满足再入接口条件。
由式(4)可知,rf一定时,E的变化只影响再入点速度vf;若后续推力只改变能量E,而动量矩H保持不变,用Δv表示终端速度的变化值,则再入点当地速度倾角的变化可表示为

即通过控制Δv,可控制ΔΘ,而Δv的上下界对应着能量的上下界(能量窗口),通过攻角方向的控制,使E∈[Emin,Emax]且动量矩H不变,即可满足再入接口条件(图3)。
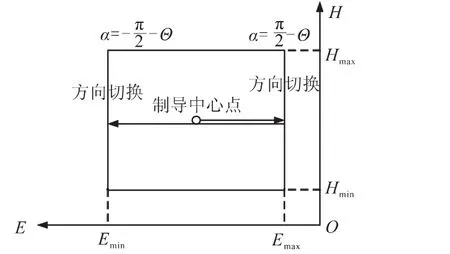
图3 方向切换与能量窗口的关系图Fig.3 Diagram of the relationship between heading angle switching and energy window
如图3所示,随机剩余燃料消耗段的制导过程如下:
(2)当到达Emax点时,攻角反向,令,此时
(3)当到达Emin点时,攻角再次反向,令-Θ,此时
(4)若仍有剩余燃料,重复步骤(2)和(3)。
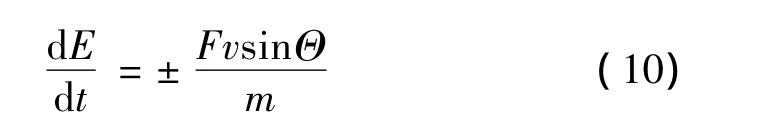
Θ的值很小,因此能量的变化过程缓慢,在随机剩余燃料较少的条件下,飞行器只需保持基本恒定的攻角即可;即使随机剩余燃料很多,也只需经过很少的切换次数,即可实现燃料的耗散。
2.2 能量耗散模型
前述模型主要解决了能量随机耗尽问题,即|vd|<ε后,在燃料耗尽时间未知的条件下,按所设计推力方向,能保证飞行器满足再入接口条件。对于多任务目标的飞行器,不同任务对应的再入条件并不完全相同,若将所有的燃料都放在|vd|<ε后进行耗尽,可能会造成推力反向的次数过多,从而增加姿态控制系统的负担。基于此,需要进一步研究闭路制导前的能量耗散模型。
若以t0表示当前时刻,tk表示标准状况下燃料耗尽的时间,则飞行器在t0时的总视速度模量为

假设在任意t时刻,飞行器的增益速度大小为vds,质量为m0,则通过式(12)可预测出消除当前增益速度所需的时间ts:
那么,可知标准状况下,消除当前增益速度的时间为tr=t+ts,以及tr时刻的剩余视速度模量We为
能量的耗散可通过改变姿态角,并按设定的姿态角变化程序来实现,采用攻角剖面的形式表示的能量耗散模型如下[8]:

式中 α0为初始攻角为攻角变化率;Δα为攻角的最大调整增量;t1、t2和t3为时间参数(见图4),可根据能量耗散要求进行设计。
由于发动机存在一定的推力偏差,预测的理论耗尽关机时间与实际关机时间也有差别,因此在能量耗散段所消耗的多余视速度模量应取总余量的一部分。
2.3 考虑能量耗散的混合制导模型
综合闭路制导模型与能量耗散模型,可得耗尽关机混合制导模型,如图4所示。

图4 耗尽关机混合制导模型示意图Fig.4 Diagram of depleted shutdown hybrid guidance model
采用该模型进行制导的基本过程如下:
(1)当t≤t3时,是能量耗散导引段,按能量耗散模型确定α(t)的规律;
(2)当t3<t≤t4时,根据速度增益制导算法确定a(t),在 t4点,|vd|<ε;
(3)当t>t4时,进入随机剩余能量耗散段,推力方向根据能量的变化进行切换,其中t5和t6分别为第一次和第二次切换时间。
3 仿真算例
以可重复使用飞行器为仿真对象,初始轨道为400 km高度的圆轨道;发动机推力F=2 400 N,最大随机偏差推力取15%,发动机有效排气速度Ve=3 000 m/s;飞行器初始质量M0=1 700 kg,其中包括燃料270 kg;再入高度 he=120 km,再入速度 ve∈[7 898,7 902],速度倾角 Θe∈[-2°,-3°]。分别采用闭路制导模型与混合制导模型对飞行器进行导引,可得仿真结果如图5、图6所示。
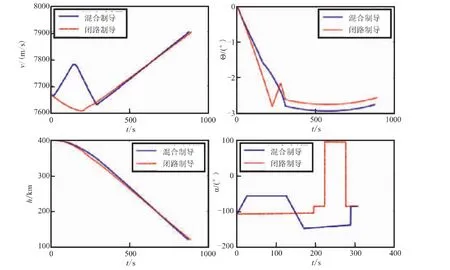
图5 飞行器状态参数与控制参数比较图Fig.5 Comparison diagram of state variables and control variables of spacecraft

图6 “动量矩-能量”变化图Fig.6 Diagram of"angular momentum-energy"
对比单纯的闭路制导方法与加入能量耗散模型的混合制导方法,由图5可知,2种方法都可将再入参数值控制在再入接口条件范围之内;采用混合制导模型能使剩余燃料耗散段的时间大为缩短,且无需做攻角的反向机动,因此对姿态控制系统的要求较低,易于工程实现;闭路制导模型在随机剩余燃料达120 kg时,攻角需要做2次反向切换,即飞行器需要做2次大角度姿态机动。
以制导中心点的能量和动量矩为基准,Ex、Hx分别表示归一化的能量与动量矩。图6所示为2种制导方法的“动量矩-能量”变化,两图中的右图是左图的局部放大。图6进一步表明,通过控制飞行器的能量变化,可控制再入参数的偏差,精度只与能量偏离制导中心点的距离有关,可通过缩小能量窗口的取值范围来提高精度,但这样会造成攻角反向的频率增大,需要根据实际情况对能量窗口进行设计。
4 结论
(1)针对可重复使用飞行器的离轨再入终端条件,提出了能量耗散与闭路制导相结合的耗尽关机制导方法。为了满足飞行器执行不同任务的再入接口条件要求,在闭路制导前先预估总视速度模量的余值,由计算所得的攻角剖面来消耗多余的能量。针对固体火箭发动机推力偏差大、随机关机时间无法预测的情况,推导了连续推力作用下飞行器能量与动量矩的变化特性,提出了随机剩余能量耗散与速度增益制导相结合的闭路制导模型。
(2)数值仿真结果表明,在推力偏差较大、剩余燃料耗散时间较长的情况下,该耗尽关机制导方法能够满足再入接口条件的要求。速度增益制导结束后,通过控制攻角,使得动量矩不变,能量在有界区域内变化的方法,较好地实现了再入点速度与速度倾角的精度要求。所得结论对可重复使用飞行器的离轨再入返回轨道设计与制导具有一定参考价值。
[1]Joosten B K.Descent guidance and mission planning for space shuttle[C]//Space Shuttle Technology Conference,Part 1,1985.
[2]Morgan C Baldwin,Ping Lu.Optimal deorbit guidance[J].Journal of Guidance,Control and Dynamics,2012,35(1):93-103.
[3]Giorgio Tumino,Enrico Angelino,Frederic Leleu,et al.The IXV project the ESA re-entry system and technologies demonstrator paving the way to european autonomous space transportation and exploration endeavours[C]//IAC-08-D2.6.01.
[4]Barry A Galman.Minimum energy deorbit[J].Journal of Spacecraft and Rockets,1966,3(7):1030-1033.
[5]Barry A.Galman.Minimum range-sensitivity deorbit[J].Journal of Spacecraft and Rockets,1971,8(2):189-190.
[6]陈洪波,杨涤.可重复使用飞行器离轨制动研究[J].飞行力学,2006,24(2):35-39.
[7]Morgan C Baldwin,Binfeng Pan,Ping Lu.On autonomous optimal deorbit guidance[C]//AIAA Guidance,Navigation,and Control Conference,AIAA 2009-5667.
[8]陈克俊.耗尽关机制导方法研究[J].国防科技大学学报,1996,18(3):35-39.
[9]康建斌,赵建亭,王明海.基于固体火箭发动机耗尽关机的混合轨道自适应制导方案研究[J].固体火箭技术,2006,29(6):407-411.
[10]胡正东,郭才发,曹渊.轨道轰炸飞行器过渡段轨道设计与制导[J].固体火箭技术,2009,32(5):473-477.
