变质心再入飞行器自适应滑模退步控制律设计①

耿克达，周 军，林 鹏

(西北工业大学精确制导与控制研究所，西安 710072)

0 引言

现代反导拦截系统对再入飞行器突防生存能力提出了更高要求，作为一种新型的飞行器变轨技术，变质心控制成为近年来研究的热点问题之一。它通过改变飞行器系统质心位置，利用飞行器高速运动产生的气动力和力矩，对飞行器进行姿态控制。与传统控制方式(主要指气动舵和RCS方式)相比，它具有以下优点［1－6］:变质心机构位于飞行器内部，保证了飞行器良好的气动外形;无需特殊解决机构的烧蚀问题;节省系统工质消耗，结构简单。

虽然变质心控制有许多优点，但在实际应用中也存在其不足。例如:为了实现对飞行器三通道的有效控制，需采用三维变质心控制。这一方面，导致系统非线性、耦合性以及不确定性非常严重，控制器设计非常复杂;另一方面，又增加了执行机构的设计难度;同时，由于飞行器轴向过载较大，使得轴向质量块所需驱动功率很大［7］。因此，本文采用一种变质心/气动舵复合控制再入飞行器构型，其中飞行器俯仰和偏航通道采用变质心控制，滚转通道采用差动舵控制。这种方式减小了变质心控制带来的各种耦合与干扰，同时又尽可能地保证了飞行器良好的气动外形。

由于变质心控制导致惯性主轴偏移，同时质量块运动引入干扰力矩和控制耦合，使得变质心再入飞行器具有更强的耦合性、非线性以及模型不确定性。因此，对变质心再入飞行器，需采用先进控制方法设计其控制律［1，8－12］。退步控制由于其独特的构造性设计过程和对非匹配不确定性的处理能力，在飞机及导弹控制系统设计得到了成功应用［7，13－14］。

本文拟将自适应滑模与退步控制相结合，研究变质心复合控制飞行器在不确定干扰下的非线性控制系统设计方法。本文首先对变质心/气动舵复合控制再入飞行器进行了数学建模;在此基础上，将系统质心移动导致的惯性主轴偏移和惯性力矩作为不确定项，对飞行器参数摄动和变质心控制引起的各类不确定性进行分析，并得到系统的仿射模型;最后，利用反馈线性化和退步控制技术，设计了飞行器三通道自适应滑模鲁棒控制器。

1 变质心再入飞行器数学模型

变质心复合控制再入飞行器构型如图1所示，将其看作为多刚体系统。其中，飞行器本体(不含滑动质量块)质心为C，质量为mC;2个滑动质量块质心分别为A和B，质量为mA和mB，初始安装位置在飞行器本体质心处，可分别沿飞行器y轴和z轴运动;系统总质量 ms=mA+mB+mC，质量比 μA=mA/ms，μB=mB/ms。

图1 变质心/气动舵复合控制再入飞行器结构示意图Fig.1 Structure of moving mass/rudder compound control reentry vehicle

采用矢量力学法，直接给出飞行器的动力学方程。其中，系统质心平动方程在再入系下描述，绕质心转动方程在本体系下描述。

质心平动方程:

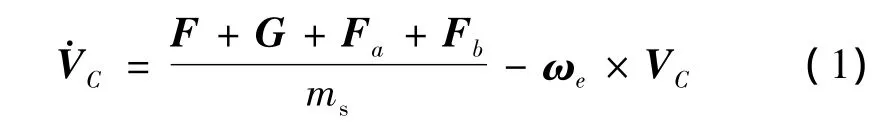
绕质心转动方程:

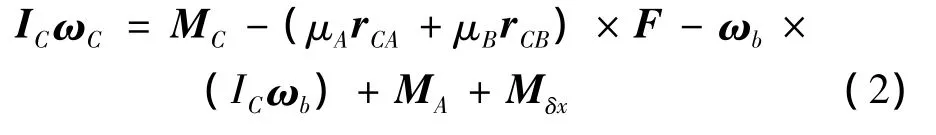
其中

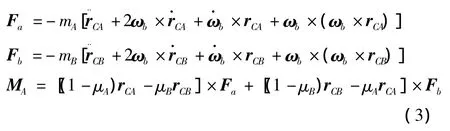
式中 VC为飞行器本体相对惯性系的速度矢量在再入系下的投影;F、MC为飞行器本体所受气动力和力矩;G为系统所受地球引力;Fa、Fb分别为两质量块运动引起的惯性力;MA为两质量块运动引起的惯性力矩;ωe为地球自转角速度矢量;ωb为飞行器相对惯性系姿态角速度;IC为飞行器本体的转动惯量矩阵;Mδx为差动舵产生的滚转控制力矩;rCA和rCB分别为两滑块相对飞行器本体质心的矢径。

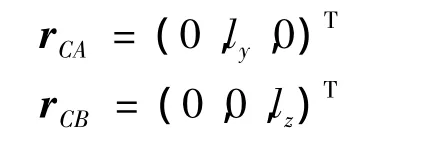
忽略地球自转和质量块运动产生的惯性力矩，并假设飞行器俯仰与偏航通道姿态角及角速度均为小量，可对飞行器姿态方程进行简化。同时，考虑到飞行器气动角α、β在实际中难以测量。因此，将其替换为实际中容易获得的法向过载ny与侧向过载nz。对于三通道稳定飞行器，其速度倾斜角γv很小，有:

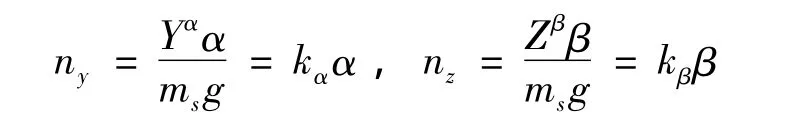
因此，可得简化后的姿态方程:

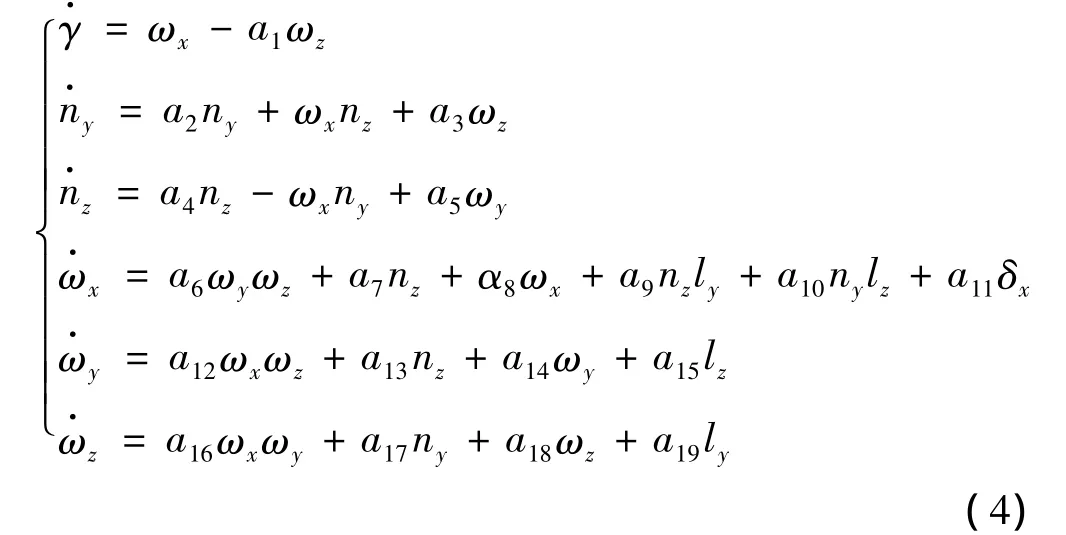
式中 ai(i=1，2，…，17)为与质量块质量、飞行器本体总体参数、气动参数以及姿态角相关的自定义系数。

对上述MIMO系统，取状态变量x1、x2，控制变量u，定义:

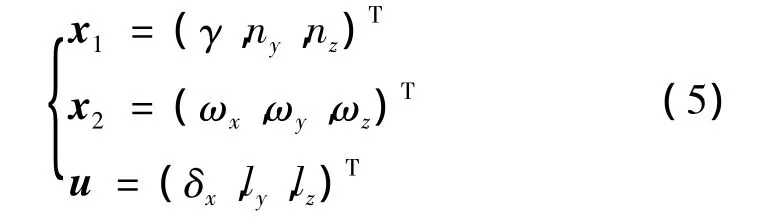
可得变质心再入飞行器标称仿射模型:

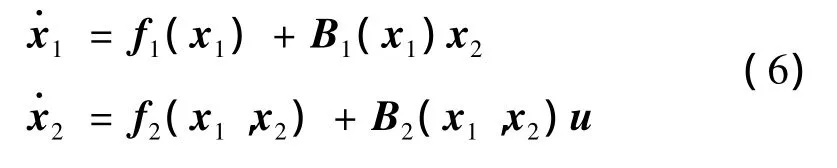
2 变质心再入飞行器摄动分析

与传统飞行器相似，变质心再入飞行器同样存在气动参数、质量参数及总体参数的摄动;同时，由于在模型简化中采用了小角度假设，因此式(6)中f1、f2、B1及B2均存在参数不确定性。

此外，由于变质心机构的引入，使得模型具有独特的不确定性。

(1)变质心机构运动引入的干扰力矩

由式(3)可知，变质心机构的位移、速度和加速度都会对系统产生干扰力，并通过系统质心偏移引入到飞行器姿态方程中。由于在有限的飞行器空间内，变质心机构的位移、速度和加速度均为时变有界量，由此引入的干扰力矩也为时变有界量。

(2)变质心机构引入的转动惯量偏差

由于变质心机构改变了飞行器总质心位置，使得飞行器转动惯量发生改变。忽略质量块自身转动惯量，变质心再入飞行器转动惯量矩阵为

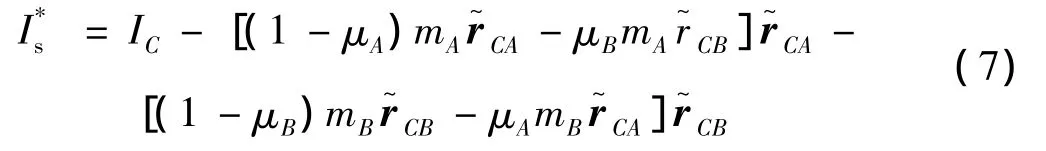
由式(7)可知，质量块运动一方面改变了主转动惯量，另一方面改变了飞行器惯性主轴，产生了惯量积，对模型引入了惯性耦合干扰。

(3)变质心机构安装位置偏差引入的不确定项

不失一般性，假设变质心机构安装位置偏差为lCA=(lCAx，lCAy，lCAz)T和 lCB=(lCBx，lCBy，lCBz)T(实际设计中，为了实现机构的正常运动，该偏差是必然存在的，且 lCAx≠lCBx≠0［7］)。因此，在设计控制器时，必须考虑该偏差引入的干扰力矩:

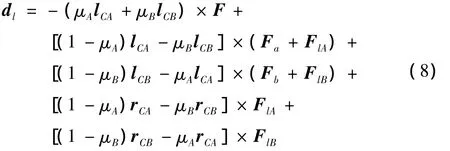
其中

(4)飞行器质心偏差引入的不确定项

相比传统控制方式，变质心控制受飞行器重压心距影响更为严重。因此，将质心偏差引入的不确定项特殊考虑。由于测量和气动烧蚀的不确定性，飞行器质心必然存在偏差。假设飞行器质心偏差lC=(lCx，lCy，lCz)T，该偏差为一缓慢变化量，可忽略其动态特性。则质心偏差引入的不确定项包括3部分:

a.飞行器本体转动惯量不确定项，其形式与式(7)类似。

b.飞行器气动力矩系数不确定项，其表达式为

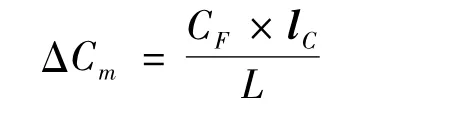
式中 L为飞行器参考长度。

由文献［5］可知，ΔCm对变质心机构的控制能力影响很大。

c.与变质心机构相对位置不确定项，其引入的干扰力矩形式与式(8)类似。

综上，可将变质心再入飞行器仿射摄动模型写为

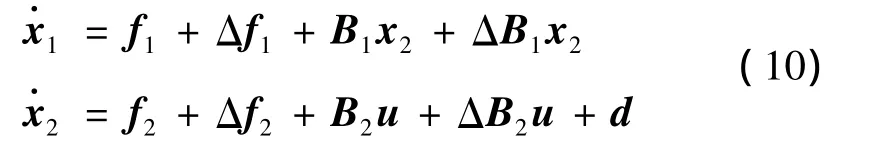
式中 Δf1、Δf2为飞行器本体气动参数和总体参数引起的摄动项;ΔB1、ΔB2为输入不确定项;d为式(1)～式(4)所讨论的变质心不确定项。

3 自适应滑模退步控制系统设计

由前文分析可知，与传统再入飞行器相比，变质心再入飞行器具有更强的模型不确定性。因此，必须对其设计高性能鲁棒控制器。

本文基于反馈线性化原理和标准退步控制思想，分别设计了其过载和姿态角速度双回路控制器。同时，为了更好地克服系统不确定性，在不确定性上界未知的情况下，采用滑模控制方法，并通过自适应算法对滑模参数进行更新，最终将其综合为一种三通道自适应滑模退步控制系统设计方法。控制系统结构框图如图2所示。

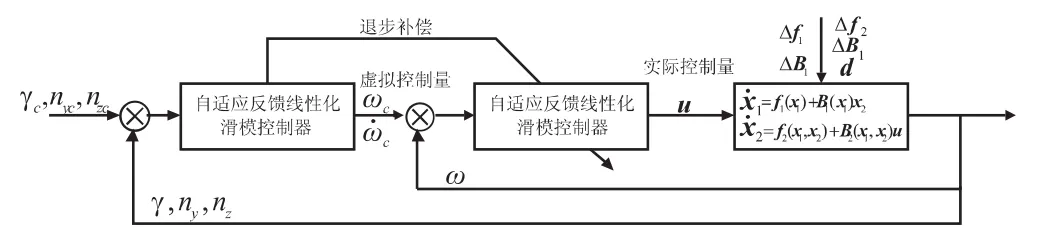
图2 自适应滑模退步控制结构框图Fig.2 Structure of adaptive sliding mode backstepping control

3.1 外环控制器设计

根据退步设计思想，首先对外环设计自适应滑模控制器。根据式(6)，取 x2=(ωx，ωy，ωz)T为虚拟控制量。

定义1:对任意向量ξ∈rn，记:

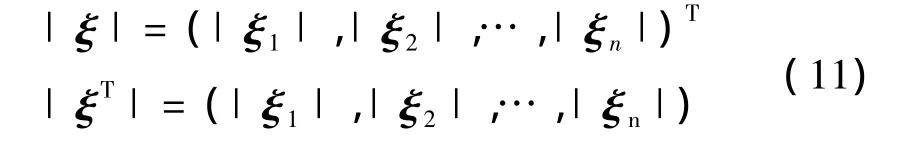
定义 2:向量 ζ，ζ∈rn，若:

则记为

由前文分析可知，外环不确定项是由飞行器本体气动及总体参数摄动引起的，且为一连续有界函数向量，根据式(11)、式(12)，有

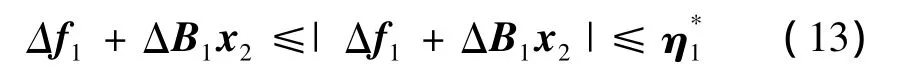
基于反馈线性化原理，设计外环动态逆控制律为

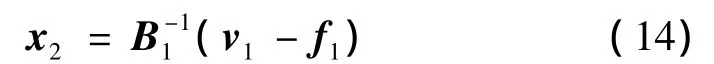
对于文中变质心再入飞行器，det(B1)≠0，故存在。将式(14)代入式(10)，外环模型可写为

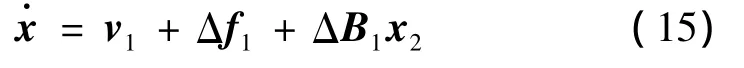
定义外环跟踪误差:

式中 x1d为外环姿态指令，通常为阶跃信号。

为实现系统的无静差跟踪，设计如下积分形式的滑模面:

结合式(15)，对式(17)进行微分，有

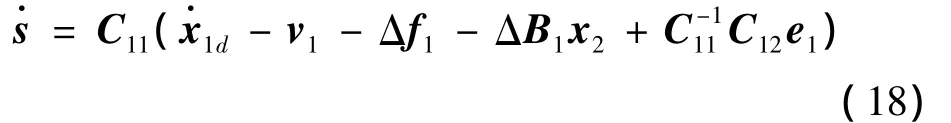
根据滑模面能达条件，采用如下指数趋近律:

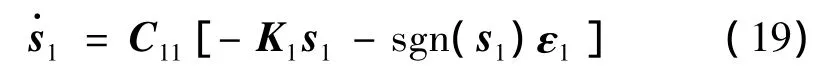
可得:

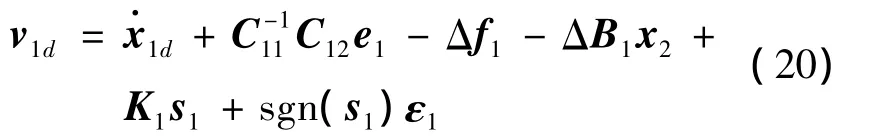
式中 sgn(s1)=diag(sgn(s11)，sgn(s12)，sgn(s13));C11、C12、K1为待设计控制参数正定对角阵，由于对模型采用了反馈线性化处理，所以各通道控制参数可独立设计。

由于系统不确定项Δf1、ΔB1不可测且上界未知，故将式(20)修正为如下自适应滑模控制律:

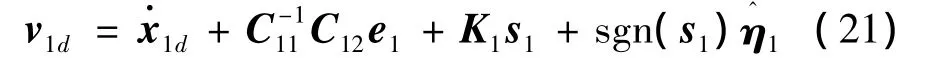
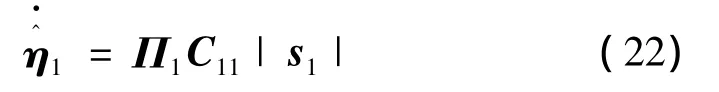
式中 Π1为更新率参数正定对角阵。

式(22)的推导见3.3节证明。于是，虚拟滑模控制律可设计为

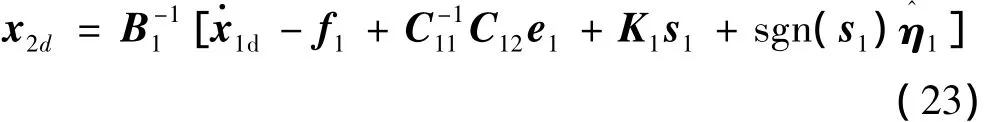
3.2 内环控制器设计

对于内环不确定项，根据式(3)，考虑到质量块位移二阶导数为非连续瞬时有界干扰。于是，内环不确定项仍为一有界函数向量，即:

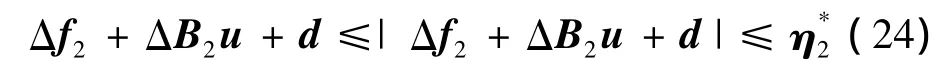
与外环控制回路类似，设计内环动态逆控制律为

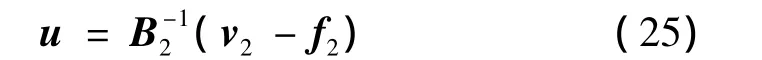
由于 det(B2)≠0，故 B－12恒存在。定义内环误差向量:

式中 x2d外环虚拟控制量。

设计内环滑模面，使内环系统状态x2跟踪虚拟控制量x2d。取

采用指数趋近律，直接给出内环自适应滑模控制律为

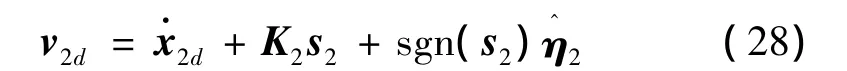
式中K2为待设计控制参数正定对角阵为虚拟控制量的变化率，可通过对x2d进行一阶滤波获得。

式中 Π2为更新率参数正定对角阵，其推导见3.3节证明。

于是实际控制指令为

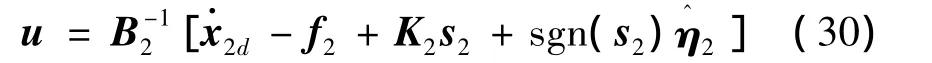
由于外环虚拟控制量x2d与实际状态量x2存在偏差e2，于是式(18)可修正为

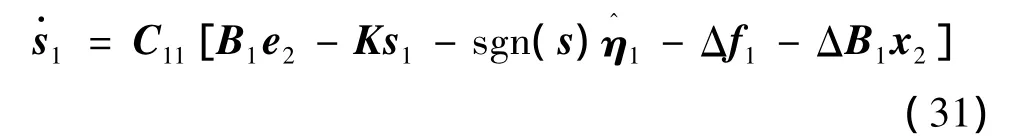
根据退步控制思想，偏差C11B1e2需通过实际控制量u在内环控制中消除，以保证闭环系统稳定。因此，将控制律式(30)修正为

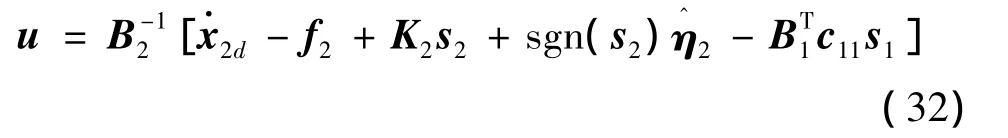
3.3 系统稳定性分析

定理:对仿射摄动模型(10)，在系统不确定性满足式(13)、式(24)的条件下，采用式(23)和式(32)所设计的控制律，以及自适应律式(22)、式(29)，则闭环系统是渐进稳定的。

证明:选取如下Lypunov函数:

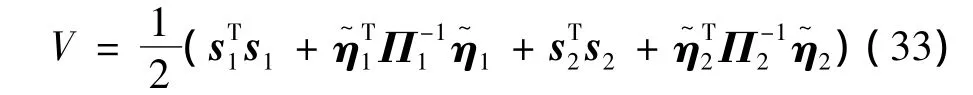
对式(33)求导，结合式(23)、式(31)和式(32)，有

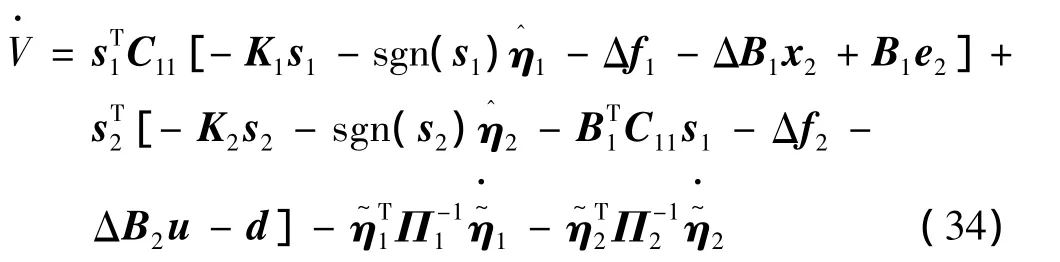
由于系统不确定项满足式(13)和式(24)，并将自适应律式(22)和式(29)代入式(34)，有

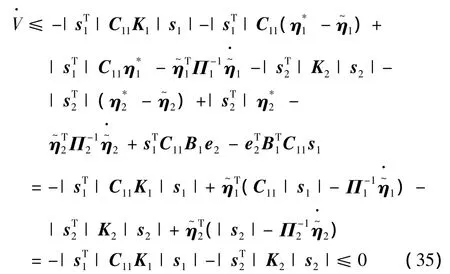
由式(35)可知，闭环控制系统是渐进稳定的。为了消除滑模控制的颤振现象，将符号函数替换为如下连续函数:

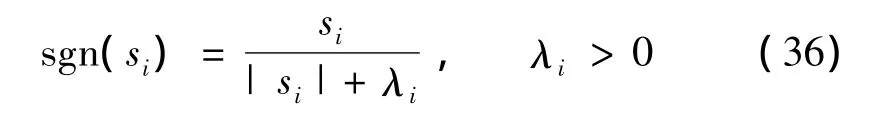
4 仿真验证

以某变质心再入飞行器为对象，验证本文方法所设计的自适应滑模退步控制器性能。

飞行器质量及总体参数为:mC=100 kg，L=1.2 m，S=0.5 m2，IC=diag(20，100，100)。变质心机构参数为 mA=mB=5 kg，|lymax|=|lzmax|=0.2 m。飞行器气动力拉偏值为20%，壳体质心偏差为lC=(0.001，0.001，0)Tm，变质心机构安装位置偏差 lCA=(0.1，0，0)Tm，lCB=(－0.101，0，0)Tm。

假设飞行器在高度25 km时飞行速度为2.5 km/s，初始姿态角为 γ0=10°，ny0=nz0=0。图 3、图 4 分别给出了跟踪阶跃过载指令和正弦过载指令的三通道控制曲线。部分控制参数如下:

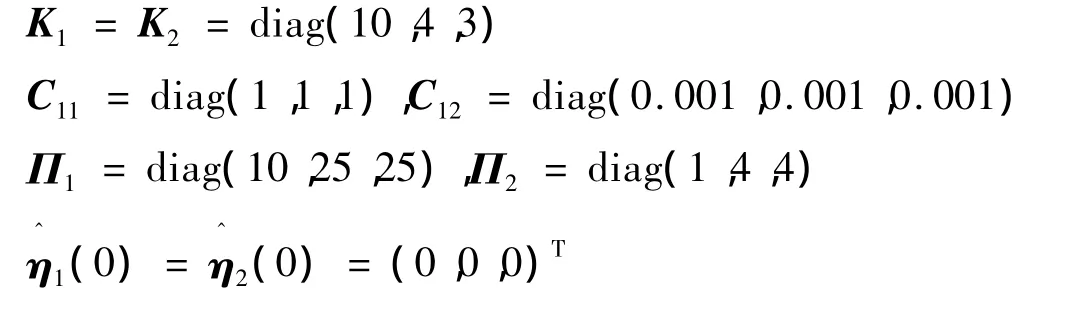
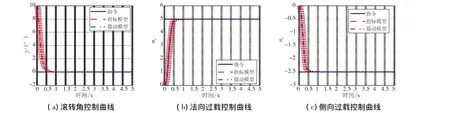
图3 变质心再入飞行器阶跃指令自适应滑模退步控制曲线Fig.3 Curves of adaptive sliding mode backstepping control for step command

图4 变质心再入飞行器正弦指令自适应滑模退步控制曲线Fig.4 Curves of adaptive sliding mode backstepping control for Sinusoidal command

分析图3、图4曲线，可得到以下结论:

(1)过载指令为阶跃信号时，采用自适应滑模退步控制，对于标称模型和摄动模型，滚转通道调节时间小于0.5 s，法向和侧向过载调节时间小于0.6 s，各通道稳态误差小于0.4%。

(2)过载指令为正弦信号时，采用自适应滑模退步控制，对于标称模型和摄动模型，滚转通道调节时间小于0.5 s，法向和侧向过载跟踪误差减小到5%以内的时间小于1 s，各通道跟踪误差小于0.7%。

(3)本文设计的自适应滑模退步控制，有效克服了变质心再入飞行器各类不确定项的影响，控制系统具有较高的快速性、鲁棒性及稳定性。

5 结论

以变质心/气动舵复合控制再入飞行器为研究对象，选取工程中实际可测的过载与姿态角速度为状态量，基于反馈线性化和退步控制技术，分别设计了过载回路与角速度回路的滑模控制律，具有以下特点:

(1)针对气动参数变化以及变质心控制引入的惯性力矩、惯量耦合、机构安装偏差等各类不确定因素，在其上界未知的情况下，通过自适应调节滑模趋近律符号项增益，来补偿其对系统的影响;

(2)当系统存在较大不确定性时，所设计控制器仍具有较高的快速性、鲁棒性及稳定性。

［1］Woolsey C A.Reduced Hamiltonian dynamics for a rigid body coupled to a moving point mass［J］.Journal of Guidance，Control，and Dynamics，2005，28(1):131-138.

［2］Vaddi S S.Moving mass actuated missile control using convex optimization techniques［C］//AIAA Guidance，Navigation and Control Conference and Exhibit.Colorado，2006-6575.

［3］Vaddi S S，Menon P K，Sweriduk G D.Muhistepping approachto finite-interval missile integraed control［J］.Joumal of Guidance，Control and Dynamics，2006，29(4):1015-1019.

［4］林鹏，周军，周凤岐.基于变质心控制的再入飞行器机动能力分析［J］.航天控制，2009，27(1):7-9，40.

［5］徐国民，李天舒，张晓宇，等.质量矩控制导弹的建模与运动分析［J］.哈尔滨工程大学学报，2011，32(12):1588-1593.

［6］魏鹏鑫，高长生，荆武兴.质量矩控制飞行器的压心不确定性问题研究［J］.航天控制，2012，30(2):39-45.

［7］高长生，荆武兴，于本水，等.质量矩导弹构型及自适应控制律设计［J］.航空学报，2010，31(8):1593-1599.

［8］Jonathan Rogers，Mark Costello.Control authority of a projectile equipped with a controllable internal translating Mass［J］.Journal of Guidance，Control，and Dynamics，2008，31(5):1323-1333.

［9］张晓宇，王子才.质量矩拦截弹的H∞鲁棒控制研究［J］.哈尔滨工程大学学报，2008，29(1):634-640.

［10］李瑞康，荆武兴，高长生，等.再入弹头质量矩复合控制系统设计［J］.航天控制，2009，27(4):43-48，52.

［11］毕开波.旋转质量矩弹头双环滑模变结构姿态控制［J］.弹道学报，2009，21(4):51-55.

［12］赵红超，王亭，范绍里.变质心自旋弹头的建模及自适应滑模控制［J］.科技导报，2009，27(5):43-46.

［13］陈宇，董朝阳，王青，等.基于自适应模糊滑模退步控制的直接力/气动力复合控制导弹自动驾驶仪设计［J］.航空学报，2007，28(增刊):141-145.

［14］高长生，荆武兴，李君龙.基于自适应反演法的质量矩导弹控制律设计［J］.兵工学报，2011，32(6):686-690.