角钢高压输电塔疲劳寿命计算与分析

孙 彤，林友新，张卓群，李宏男，李东升，任 亮

（1.大连理工大学 建设工程学部，辽宁 大连 116024；2.广东电网公司电力科学研究院，广东 广州 510080）

0 引言

疲劳破坏是指结构使用过程中疲劳积累，材料在正常应力循环作用下逐渐硬化，最终由微裂缝到断裂的过程。工程结构因材料疲劳损伤而破坏是结构破坏的主要形式和设计内容之一。对于输电塔线结构而言，以往的结构设计侧重于强度控制，对输电塔的构件材料疲劳损伤则很少考虑。输电线塔等高耸钢结构由于长期暴露在自然环境中，极易受到发生频率很高的微风的作用，这种随机脉动风荷载对结构构件反复作用会引起裂纹的萌生，并随着作用时间的持续，裂纹不断扩展以致最终发生疲劳破坏引发工程安全事故。

基于断裂力学和疲劳裂纹扩展理论的损伤容限法是计算疲劳寿命的一类重要方法，该方法在航空航天、核工业等领域应用较为广泛，并有着很好的效果，但在输电塔结构中的应用还很少。Paris［1］提出了描述裂纹扩展速率的幂函数公式，Dolinski［2］等将其应用于随机变幅疲劳问题。随着对疲劳问题研究的深入，人们逐渐认识到材料的疲劳是一个有着较大统计分散性 的 过 程［3］，Dolinski［4］、Bogdanoff和Kozin［5］、Lin和Yang［6］、Dominguez［7］等人引入了随机裂纹扩展的概念，并建立了不同的统计模型。Yang和Manning［8］分别采用Monte-Carlo模拟法和二次矩近似法将对数正态扩展模型应用于飞机结构设计，取得了很好的效果。屠海明和邓洪洲［9］、徐志宏等［10］应用该方法计算了桅杆结构的风振疲劳寿命，但没有考虑参数统计的分散性。

本文基于损伤容限理论和断裂力学理论，对500kV输电塔结构进行疲劳寿命分析，重点研究角钢铁塔塔材和节点板焊缝在风力作用下疲劳问题，以及输电塔结构在风力作用下疲劳寿命的评定方法，其分析步骤如图1所示。

图1 输电塔风振疲劳分析步骤Fig.1 Analysis steps of transmission tower wind vibration fatigue

1 风荷载模拟

本文研究的500kV输电塔结构的风环境取南京地区风玫瑰图，对输电塔结构进行了疲劳计算。

在实际的应用中，对输电塔每个模拟区域简化为一个模拟点进行风荷载的模拟，其具体位置如图2所示，参数如表1所示。计算时导线上每一点的风速时程均与悬挂点处风速时程相同，忽略导线各点的高度差异对风荷载时程的影响。

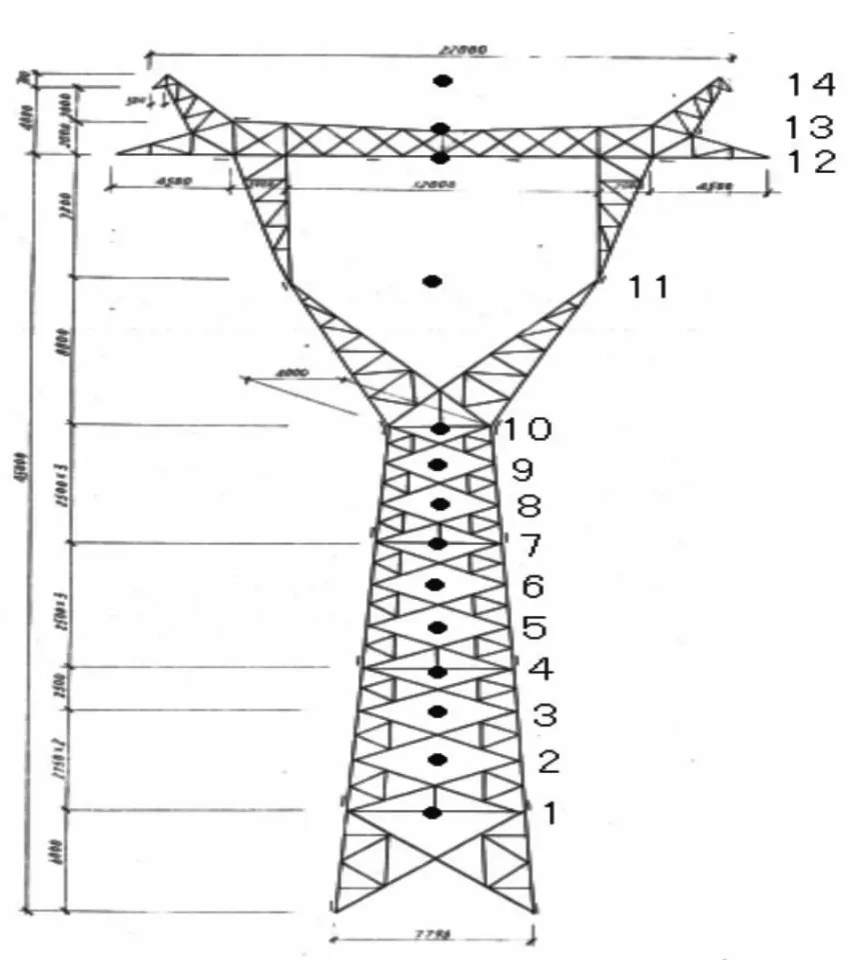
图2 输电塔模型风荷载模拟点位置Fig.2 Simulation point location wind load

表1 输电塔风荷载模拟点高度参数

与脉动风模拟相关的参数取值如下：

①10m处平均风速V=20m／s，地面粗糙长度Z0=0.2m；②时程总长t=300s，时间步长△t=0.25s，截止频率ωu=2Hz，频率范围等分数N=1024；③顺风向风速谱选取Kaimal谱，常数取为0.4，指数衰减系数，Cz=10。经过模拟，得到图2中各个位置点的风速时程曲线，如图3、4所示。

为了验证模拟方法的有效性和可靠性，应对模拟风速场的功率谱特征与目标风速谱进行比较，考察模拟风场与目标函数相吻合程度，模拟点2和10风速功率谱比较如图5所示。由图可见，模拟风速谱的谱线趋势与目标谱线是一致的，其谱线的总体均值与目标谱也很接近，这表明模拟方法与所取参数是合理有效的。

图3 模拟脉动风第2点风速时程Fig.3 Wind velocity time history of point 2

图4 模拟脉动风第10点风速时程Fig.4 Wind velocity time history of point 10

图5 模拟点脉动模拟风谱与目标风谱比较Fig.5 Pulsing simulation wind spectrum and the target spectrum

2 输电塔结构非线性动力分析

采用前述方法，得到了塔身各节点的顺风向风荷载时程，利用SAP2000中的时程分析模块对输电塔体系进行了风振响应的时程分析。时程分析依然是以在自重作用下的非线性静力分析结果作为初始状态，在此基础上进行动力分析。

对输电塔几个典型杆件单元进行疲劳寿命分析，危险部位如图7所示。根据钢结构规范，杆件32单元采用第2类连接方式C＝3.26×1012，β＝4，极限强度343Mpa。杆件1401、1402、1411、1412、1255、1256、1265、1266、837和1151单元等采用第8类连接方式C＝0.41×1012，β＝3，极限强度343Mpa。

图6 输电塔疲劳分析模型Fig.6 Model for transmission tower

图7 输电塔典型部位示意图Fig.7 Typical parts of power transmission tower

3 雨流法分析

对输电塔体系进行不同风向和风速下的时程分析，可以得到关键杆件端部的内力时程。运用前面所述的雨流计数法［11］对所得的关键部件应力时程进行应力循环计数，可以得到各风向和风速下的平均应力，再利用公式（12）得到等效应力幅。通过统计出各方向、各风速下结构构件或节点连接的等效应力幅值及相应的循环次数。这里以输电塔的关键杆件1401号单元为例，图8-12表示1401号单元在输电塔受到10米高度风速为v＝30m／s，风攻角为0度、22.5度、45度、67.5度、90度风载作用时的Von Mises应力时程曲线，时长为60s。图13-17表示应力幅统计情况。

图8 风攻角0度时应力时程曲线Fig.8 Time histories of stress when wind attack angle is 0°

图9 风攻角22.5度时应力时程曲线Fig.9 Time histories of stress when wind attack angle is 22.5°

图10 风攻角45度时应力时程曲线Fig.10 Time histories of stress when wind attack angle is 45°

图11 风攻角67.5度时应力时程曲线Fig.11 Time histories of stress when wind attack angle is 67.5°

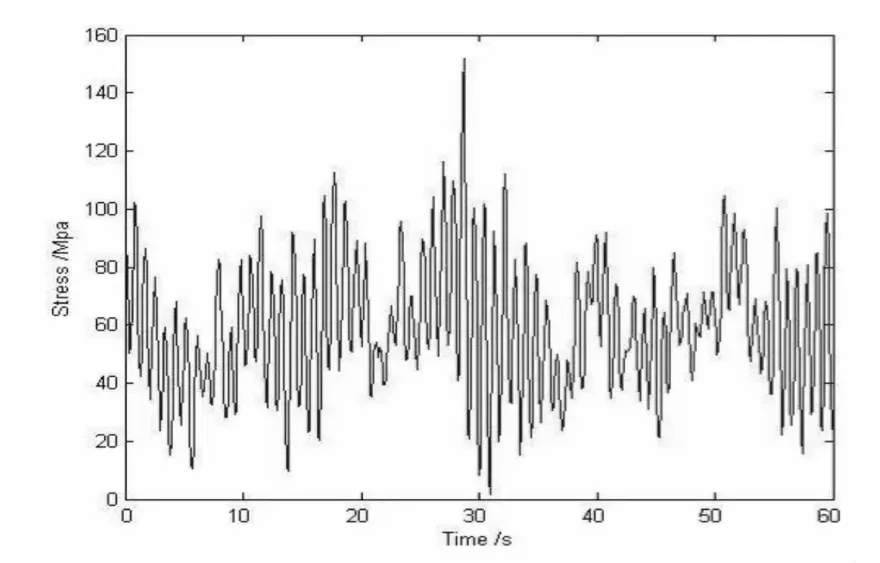
图12 风攻角90度时应力时程曲线Fig.12 Time histories of stress when wind attack angle is 90°

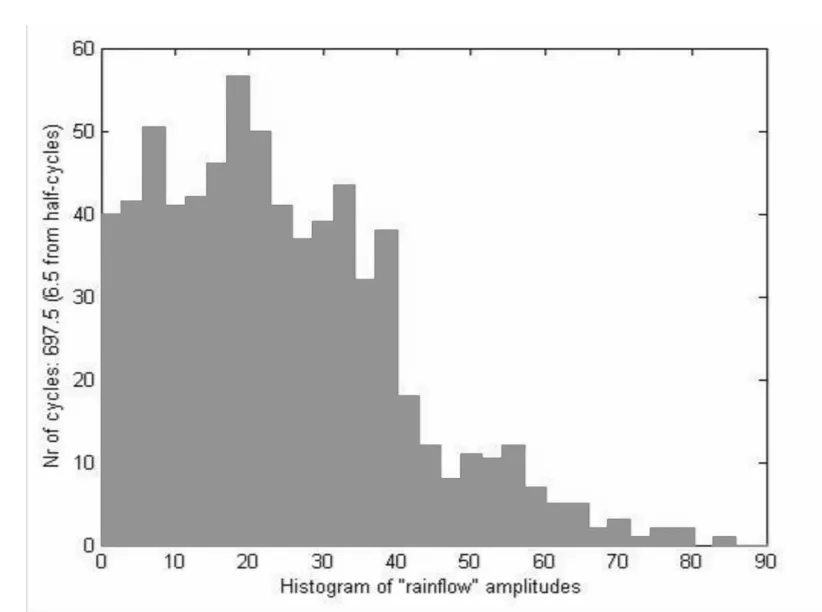
图13 风攻角0度时应力雨流统计Fig.13 Rainflow result of stress when wind attack angle is 0°

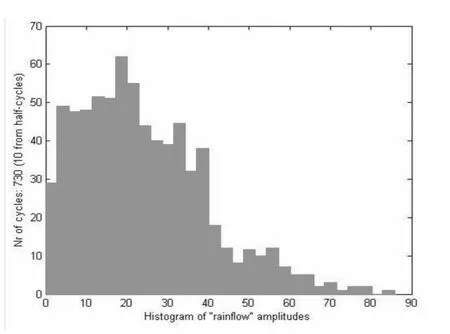
图14 风攻角22.5度时应力雨流统计Fig.14 Rainflow result of stress when wind attack angle is 22.5°

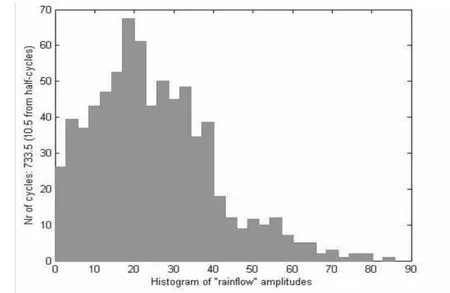
图15 风攻角45度时应力雨流统计Fig.15 Rainflow result of stress when wind attack angle is 45°

图16 风攻角67.5度时应力雨流统计Fig.16 Rainflow result of stress when wind attack angle is 67.5°

图17 风攻角90度时应力雨流统计Fig.17 Rainflow result of stress when wind attack angle is 90°

4 基于钢材裂纹扩展的疲劳寿命预测方法

在钢结构的疲劳破坏过程中，裂纹尖端塑性区域通常很小，因而线弹性断裂力学方法能较好地适用。用该种方法考察疲劳问题，首先是分析裂纹扩展速率da／dN，在线弹性断裂力学范围内，静载作用下应力强度因子K能恰当地描述裂纹尖端的应力场强度。大量的疲劳试验证明，K也是控制裂纹扩展速率da／dN的主要参数，且与应力强度因子幅度ΔK存在一定的函数关系，这里ΔK是由交变应力最大值σmax与最小值σmin所计算的应力强度因子值之差，即ΔK＝Kmax-Kmin。Paris最早给出了da／dN与ΔK之间的经验关系式（Paris定律）［12］。

式中，c和n为与材料有关的常数。确切地说，n不仅与材料有关，还与平均应力及环境有关，为简便起见，在近似计算中不考虑这些因素的影响。

如己知原始裂纹尺寸a0及裂纹临界尺寸ac，则可以按下式得到疲劳循环次数：

一般情况下，有：

式中，Y为表征含裂纹构件几何形状的无因次系数，代入式（2）可得：

对于初始裂纹尺寸a0的取值，文献［13］建议在没有实测资料的情况下，取0.05～0.5mm；裂纹临界尺寸则根据材料的断裂韧性确定。

以上是塔材和节点板焊缝在常幅疲劳荷载作用下估算裂纹扩展寿命的一般公式，在变幅加载疲劳中，需要对应力幅值加以折算：

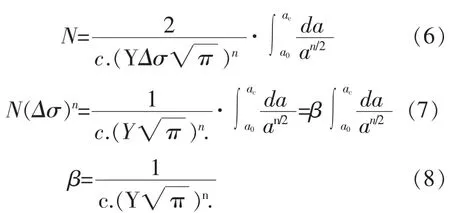
根据Miner规则的假定［14］，不同应力幅对结构作用的先后顺序不影响疲劳寿命，可以假设：

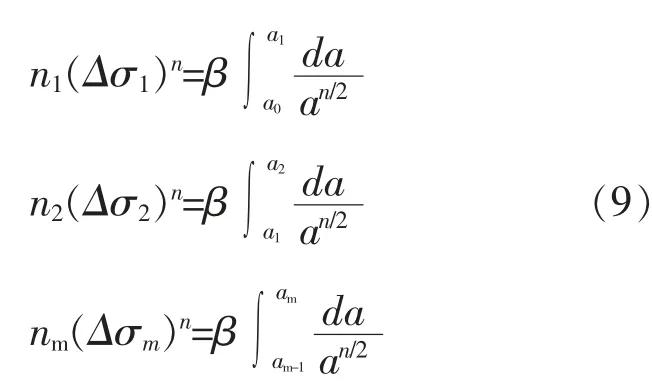
将上面各式左右两边各自相加，可得

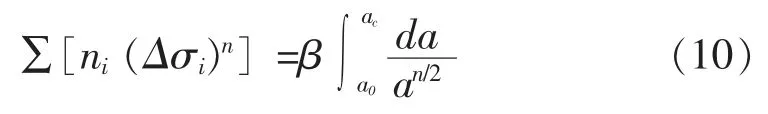
又根据等效应力幅的概念，有

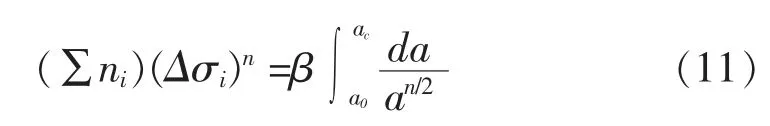
以上两式相比较，可以得到等效应力幅Δσc为：

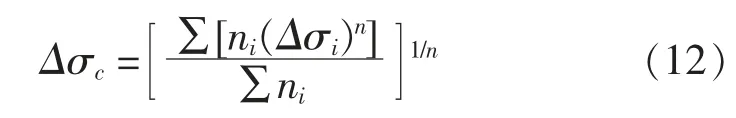
根据上述得到的构件应力时程，利用（12）式将非零均值的应力幅值换算为零均值的应力幅值，然后利用（4）式得到各零均值应力幅值对应的疲劳破坏循环次数；最后根据Miner线性疲劳累积损伤理论获得结构各构件在计算时段内的疲劳累积损伤。

根据Miner疲劳损伤准则，把各个角度各个风速下1401单元的损伤值相加，得到其总损伤值0.5335。由酒杯塔已使用的年数为21年，故其疲劳累计损伤使用年限为21／0.5335＝39.363年。剩余使用年限为39-21＝18年。计算结果在表2中给出。

表2 输电塔在风荷载单独作用下疲劳寿命

前一部分，在进行输电塔疲劳分析仅考虑风荷载这一个因素，而忽视了由于钢材安装、浮冰、台风等恶劣天气作用累计损伤的影响，导致结构计算出的剩余年限值偏大，与实际情况存在一定的差距。为了更加准确的反应输电塔因环境荷载引起的结构疲劳损伤问题，根据当地的气候条件，将一次性强荷载作用情况（台风、覆冰、安装等荷载工况）转化为与风荷载工况一致的分布概率和荷载谱，其中台风荷载按照每年2-3次，风速33m／s，持续时间一般24小时，最大考虑按48小时计算。覆冰荷载按照30年一遇设计，覆冰厚度为5mm，一般持续时间一周。安装荷载应按10m／s风速、无冰、相应气温的气象条件等，安装时间为一个工作日。计算结果如表3所示。

与表2结果对比可以看出，输电塔在多种环境荷载作用下的疲劳寿命比单一风荷载作用下的寿命要短，因此应注重多环境因素作用下的疲劳损伤影响。然而这种风荷载仍然是影响输电塔结构疲劳寿命的主要因素，粗略估算时可仅考虑这种荷载的影响。

5 结论

本文基于线性疲劳累积损伤理论和断裂力学理论，从时域方面讨论了输电塔风振疲劳的计算方法，得到如下结论：

（1）输电塔结构的时域疲劳分析可以遵循图1所示的思路进行，在给定材料性能的基础上，考虑风向和平均风速分布的影响后，基于塔线体系的风振时域分析和雨流法可以给出任意疲劳验算点的理论疲劳寿命和剩余疲劳寿命。

（2）通过对角钢铁塔塔材和节点板焊缝在风荷载及其它重要荷载作用下疲劳问题的研究和实例的结果表明，防范输电塔疲劳破坏尤为必要。

（3）风荷载是输电塔疲劳寿命的主要致因，粗略计算时亦可只考虑风荷载作用。

［1］Paris P C，Gomez M P，Andrson W E.A rational analytic theory of fatigue［J］.The trend in engineering，1961，（13）：9-14.

［2］Dolinski K.Fatigue crack growth with retardation under stationary stochastic loading［J］.Engineering fracture mechanics，1987，（27）：279-290.

［3］Schijve J，Fatigue predictions and scatter，Fatigue fracture and engineering material structures，1994，（17）：381-396.

［4］Dolinski K.Formulation of a stochastic model of fatigue crack growth［J］.Fracture engineering of material structures，1993，（16）：1007-1019.

［5］Bogdanoff J L，Kozin F.Probabilistic models of cumulative damage［M］.Wiely，NewYork，1985.

［6］Lin Y K，YangJ N.A stochastic theory of fatigue crack propagation［J］.AIAA，1985，（23）：117-124.

［7］Dominguez J，Zapatero J，Moreno B A statistical model for fatigue crack growth under random loads including retardation effects，Engineering fracture mechanics，1999，62：351-369.

［8］Yang J N，Manning S D.Stochastic crack growth analysis methodologies of rmetallicstrueurtes，Engineering fracture mechanics，1990，37：1105-1124.

［9］屠海明，邓洪洲.桅杆结构风振疲劳分析阴［J］.四川建筑科学研究，2001，27（2）：6-8.

［10］徐志宏，邓洪洲.桅杆结构纤绳与杆身连接拉耳风致疲劳寿命预测［J］.特种结构，2004，（21）：25-27.

［11］王秉刚.汽车可靠性工程方法［M］.北京：机械工业出版社，1991.

［12］查小鹏.高耸结构风致疲劳安全预警的理论和方法［D］.武汉：武汉理工大学，2008.

［13］颜明忠.桅杆结构风振动力响应理沦及实验研究［D］.上海：同济大学，1998.

［14］查小鹏.高耸结构风致疲劳安全预警的理论和方法［D］.武汉：武汉理工大学，2008.