预应力损伤对混凝土梁桥自振频率的影响分析
2013-08-23程浩彭凯
程浩 彭凯
(重庆交通大学土木建筑学院,重庆 400074)
预应力技术在桥梁工程结构中的应用已经有70年的历史,发展至今,当前全世界的桥梁中有70%以上都使用了PC结构。随着社会的发展,交通量的日益增大,很多PC结构桥梁出现了预应力损失过大、结构裂缝损伤等病害,如何能比较快速准确的对这些病害进行识别成为现今工程界研究的热点。
基于振动测试的结构损伤识别是建立在损伤前后结构的动力特性会发生变化这一原理基础上,随着它在普通钢筋混凝土结构损伤检测中的应用越来越广[1,2],该方法在大跨径桥梁健康监测和安全评估领域日益受到国内外研究者的关注。
关于预应力衰减变化的动力识别问题,国内外学者的认识还不完全一致:1994 年,M.Saiidi,B.Douglas和 S.Feng通过预应力简支梁桥动力试验之后,认为预应力混凝土简支梁的频率随着预应力的增大而增大,同时预应力对频率的影响幅度较小[3];而A.DallAsta和Dezi则通过理论分析认为,预应力对频率的影响很小,可以忽略[4]。本文以Midas civil有限元仿真模拟为手段,开展预应力混凝土简支梁桥模型和连续刚构桥模型的动力特性参数分析,计算对比预应力大小对预应力混凝土梁桥自振频率的影响,探讨通过动力识别方法监测预应力衰减变化的可行性。
1 理论分析
经典匀质轴心受力杆件自振频率理论分析计算简图见图1[4]。

图1 轴心力作用下的匀质杆
轴心力N(压正拉负)作用下,基于平截面假定,建立杆件的自由弯曲振动微分方程为:
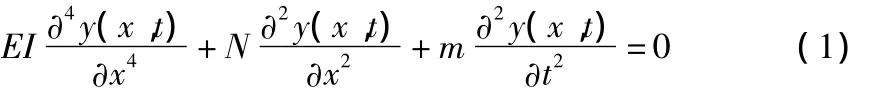
其中,y(x,t)为杆件振动时各点的挠度;N为轴向作用力;m为梁的分布质量;EI为杆件截面抗弯刚度。
对于等截面匀质杆件,可通过对式(1)进行求解得梁的自振频率为:

其中,n=1,2,3…;EI为杆件截面的抗弯刚度;L为梁长。
从式(2)中可以看出,等截面匀质杆件的自振频率随着轴向压力的增大而降低,随着轴向拉力的增大而提高。对于预应力混凝土梁桥,如果将预加力视为作用在梁上的轴向压力和偏心弯矩,那么通过上面的分析可知,预应力混凝土梁桥的自振频率会随着预应力损失的累积而提高。
2 预应力对混凝土简支梁自振频率的影响
本节利用有限元模型分析预应力变化对混凝土简支梁自振频率的影响。预应力混凝土简支梁原型取文献[5]所给的设计算例[例4-2],其主要参数为:主梁标准跨径30 m,主梁高度1.96 m,截面尺寸详见图2。
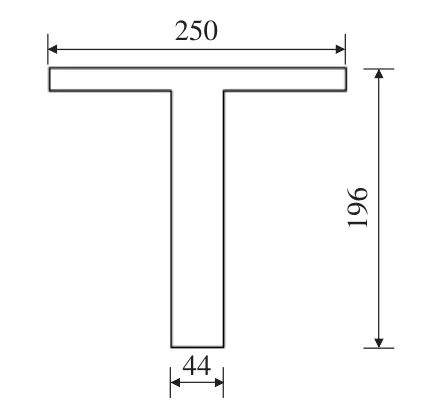
图2 T梁截面示意图(单位:cm)
在用Midas civil 2010对预应力混凝土简支梁桥进行有限元分析时,材料参数如下:国标 C50混凝土弹性模量 E=3.45×104N/mm2,泊松比 v=0.2,容重为 2.6 ×104N/mm3。在有限元模型中,混凝土简支梁采用空间梁单元,这种单元类型以铁摩辛柯的梁理论(垂直于中和轴的截面,在变形后保持平面形状,但不一定要继续垂直于中和轴)为基础,分析时考虑剪切变形。预应力采用初始单元内力的方式施加在全部梁单元上,本例预应力钢束采用4束5φj15.2钢束,张拉控制应力取0.75fpk=1 395 MPa。简支梁边界条件一端约束X,Y,Z三个方向的位移自由度(X为沿梁长方向,Y为梁宽度方向,Z为梁高方向),另一端约束Y,Z方向的位移自由度,两端同时约束X,Z方向的转动自由度;进行自振频率计算使用多重ritz法。建立的有限元仿真模型见图3,共68个单元。
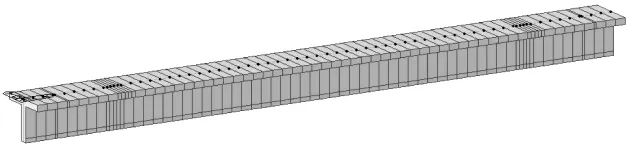
图3 简支梁有限元模型
采用上述有限元模型进行预应力混凝土简支梁模态分析,自振频率计算结果见表1。

表1 不同预加力值下简支梁频率值

图4 不同预应力衰减下简支梁桥各阶频率的相对变化率
表1中预应力衰减程度表示有限元模型初始单元内力减小的百分比,0表示无降低,其梁单元初始单元内力为施加0.75fpk张拉应力(fpk=1 860 MPa)时有限元模型求得的初始单元内力,100%表示无预应力的状态。相对变化率都以预应力无衰减为基准,例如预应力衰减10%时1阶频率的相对变化率=│预应力衰减10%时1阶频率值-预应力无衰减时1阶频率值│/预应力无衰减时1阶频率值×100%。由表1的数据可看出,预应力简支梁的频率随着预应力值的衰减而提高,这与理论分析较符合,预加力从100%衰减到无预加力状态时,1阶频率降低了1.565%,可见预应力的衰减对预应力简支梁自振频率的影响相当小。由图4的比较分析,简支梁竖向自振频率相对变化率随着阶数的增加逐渐变小,当预加力值从100%衰减到无预加力时,简支梁第5阶竖向自振频率的相对变化率仅为0.107%。通过表1的数据以及图4的分析可知,预应力变化引起的简支梁自振频率改变相对微弱,而且对于随着自振频率阶数的提高,这种改变可以忽略不计。

图5 连续刚构桥有限元模型
3 预应力对连续刚构桥自振频率的影响
通过上一节的有限元分析可知,预应力的变化对于等截面混凝土简支T梁的自振频率有一定的影响,为了分析预应力衰减对于刚度较大的连续刚构桥自振频率的影响,本文利用Midas civil 2010建立某三跨预应力混凝土连续刚构桥有限元模型来进行模态分析。连续刚构桥原型取自文献[6]实例五,基本参数如下:该桥为75 m+130 m+75 m的三跨预应力混凝土连续刚构桥,主墩为双薄壁柔性墩;主梁采用单箱单室,箱梁根部高7.8 m,跨中及边跨端部高3.0 m,梁高采用1.8次抛物线变化;箱梁采用C50混凝土,主墩采用C40混凝土。主梁各梁段采用空间梁单元进行模拟,这种单元类型以铁摩辛柯的梁理论(垂直于中和轴的截面,在变形后保持平面形状,但不一定要继续垂直于中和轴)为基础,分析时考虑剪切变形。预应力与前节一样,通过初始单元内力的方式进行模拟,对于连续刚构桥,各个梁单元的初始单元内力是不同的,通过Midas civil 2010的预应力荷载模块计算梁单元初始内力,然后再将计算所得的初始单元内力施加到各个梁单元上模拟预应力,通过所有初始单元内力按一定比例下降来模拟预应力的衰减。有限元模型共114个梁单元,见图5。
采用上述有限元模型进行连续刚构桥模态分析,结果见表2。

表2 不同预应力衰减程度下连续刚构桥频率值
由表2的数据可看出,连续刚构桥的频率随着预应力衰退而提高,当预应力衰减35%时,1阶频率增加了0.928%,与上节简支梁分析结果相比,预应力大小对连续刚构桥振动频率的影响稍明显,但是即使预应力降低为0,频率值的相对变化率也仅仅为3.06%。而通过图6可看出,连续刚构桥竖向自振频率相对变化率随着阶数的增加逐渐变小,当预应力值衰减35%时,连续刚构桥第5阶竖向自振频率的相对变化率仅为0.236%。通过上述分析可知,预应力衰退引起的连续刚构桥自振频率改变非常微弱,而且随着自振频率阶数的提高,这种影响越来越小。而对于实际桥梁,它在服役时处在现场风、环境振动等干扰下,如果采用动力识别方法监测加速度等动力信号时必然面临复杂的噪声问题,因此,想要利用现有技术在实际工程中通过自振频率的变化来识别结构预应力的变化、衰减,很难做到。

图6 不同预应力衰减连续刚构桥各阶频率的相对变化率
4 结语
本文通过有限元方法,采用初始单元内力的方式模拟不同预应力值下混凝土简支梁,分析结果表明:混凝土梁桥的竖向自振频率随预应力衰减而提高,且随着阶数的增加,这种影响会越来越小,对于刚度越大的混凝土梁桥,预应力衰减导致的自振频率的变化会略明显,但是这种变化仍比较微弱。因此对于处在复杂环境中的服役期桥梁,无法将自振频率的变化作为监测预应力衰减的有效指标。
[1]张瑞云,曹双寅.基于振动的大型工程结构损伤识别策略研究[J].工业建筑,2005,35(S1):958-961.
[2]杨秋伟.基于振动的结构损伤识别方法研究进展[J].振动与冲击,2007,26(10):87-89.
[3]Saiidi M,Douglas B,Feng S.Prestress force effect on vibration frequency of concrete bridges[J].Journal of Structural Engineering,1994,120(7):2233-2241.
[4]A Dall’Asta,LDezi St.Discussion about“Prestress force effect on vibration frequency of concrete bridges”[J].Journal of Structural Engineering,1996,122(4):458.
[5]房贞政.预应力结构理论与应用[M].北京:人民建筑工业出版社,2005:72-85.
[6]邱顺东.桥梁工程软件Midas Civil应用工程实例[M].北京:人民交通出版社,2008:79-93.
