忆阻器混沌电路的仿真

张宇琪，孙立山

(哈尔滨工业大学1.控制科学与工程系，2.电气工程系，黑龙江哈尔滨 150001)

1971年，华裔科学家蔡少棠提出了忆阻器的概念［1］。2008年HP公司发现了一种用TiO2掺杂后得到的纳米级电子元件，而这种元件的性质恰好符合忆阻器的定义，于是制成了这种忆阻器［2］。

HP忆阻器发现后不久，美籍学者Itoh和蔡少棠提出了一系列忆阻器电路用来替换蔡氏二极管，得到了忆阻器混沌电路［3］。不过，人们重点研究的是一种光滑连续的三次函数磁控型忆阻器，物理上并未实现。虽然忆阻元件尚处在探索阶段，但HP忆阻器已经物理实现，只是尚未走进普通实验室。因此，使用仿真软件进行仿真是有意义的。本文根据HP实验室提供的实物测试数据及相关理论，以及文献［4］给出的改进数学模型，将HP忆阻器应用于蔡氏电路，得到了基于忆阻器的混沌电路。我们通过调整参数，并用Matlab和Orcad进行了仿真，得到了不同于以往的混沌图形。

1 HP忆阻器概述

蔡少棠给出的荷控型忆阻元件的数学模型为

式中，q为电荷量，φ为磁通量，M(q)为忆阻器阻值。

HP实验室给出的忆阻元件的基本模型如图1所示。其中D为忆阻器的长度，w表示元件的掺杂宽度，总阻值R为掺杂部分阻值与非掺杂部分阻值之和。w=0和w=D时忆阻器的极限阻值分别用Roff和Ron表示。掺杂宽度w随外电场改变，u＞0时有向右的电流通过元件内部，w增大，R变小;u＜0时有向左的电流通过元件内部，w减小，R变大。

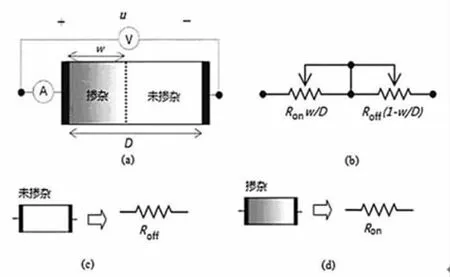
图1 忆阻元件的基本模型

据此，HP实验室给出的流控型忆阻元件的数学模型为

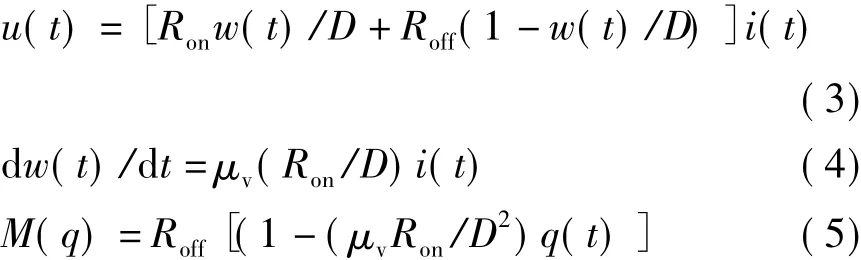
其中，μv是表示离子在均匀场中移动速率的常数，约为 10-14m2s-1V-1，通常 Roff/Ron=102-103。

当Roff≪Ron时，可近似用式(5)计算忆阻器阻值。正如文献［2］所说，人们在寻找忆阻器的时候总是想着磁场对于电阻的影响，而实际上，只要M(q)随q改变而改变即可。HP忆阻器的特征为:磁通量φ并没有起明确的作用;掺杂宽度w是有界的，在0至D之间。以往的研究都没有同时具备这两个特征，因此并非典型的HP忆阻器。

忆阻器中的状态变量选择值得思考。按照文献［3］，蔡少棠将电荷q或磁通φ视为状态变量，列出了状态方程。而HP实验室认为在不考虑边界条件的情况下，状态变量为掺杂宽度w(t)，正比于q(t)。由电路知识得，控制量为状态变量，因此将状态变量取为r=w/D，这与取为w是一样的。则可用下面各式表示HP忆阻器的特性:

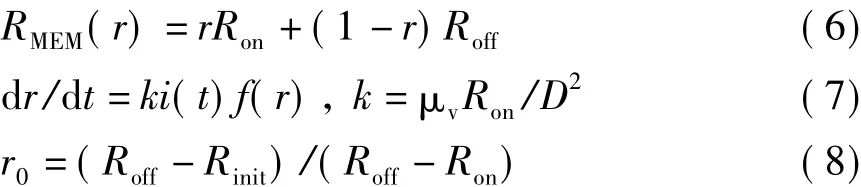
其中，Rinit为初始时忆阻器的电阻值。由HP实验室试验数据粗略计算，可取长度为10nm的忆阻器，其k=104s－1A－1，Roff=40kΩ，Ron=0.1kΩ。

文献［2］还提到了边界情况，即当完全掺杂或完全未掺杂时的情况。文中给出了一种通俗的假设:当上述两种情况发生时，电阻保持不变，直到离开边界范围。在纳米级范围，很小的电压能产生巨大的电场，进而在离子移动过程中产生重要的非线性。这种非线性在边界处表现得更加明显，使得掺杂与非掺杂分界线移动速度逐渐趋于零，这一现象称为掺杂漂移，可以用窗函数f(r)表示。虽然能用来解释HP忆阻器的确切的窗函数f(r)并没找到，但已有一些模型供可我们使用。HP实验室在研究时给出了一种假设:w(1－w)/D2。依据这种假设，给出了仿真的u-i关系图，并与实际测量的关系图进行比较，两者十分接近。但文献［2］中同时说，不考虑非线性漂移的情况也有报道。因此，文中指出，可以根据丰富的u-i关系图来分析边界问题。

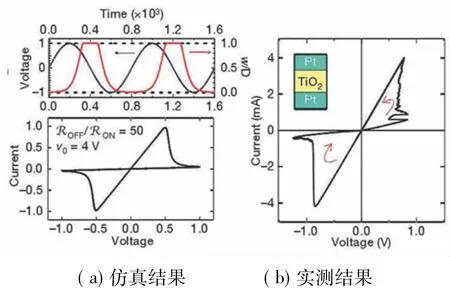
图2 HP实验室滞后环的u-i关系

在文献［4］中给出了f(r)的另一种形式:

其中，p是一个正整数。若p较小，则分界线快要达到边界时速度逐渐减小到0;若p越大，这种控制速度的功能就越不明显;p趋于无穷，则起不到边界限制的作用，本文采用了这种模型。

事实上，非线性漂移很复杂，后续的学术报道中指出，即使经过同一位置，分界线朝两个方向的速度并不相同，且移动速度还和电场强度有关。因此，上述模型都是简单模型，不可能完全表征HP忆阻器，但这对我们仿真分析已经足够了。

2 忆阻混沌电路的Matlab仿真

我们可用HP忆阻器模型与两个电感、一个电容和一个负电阻构成一个混沌电路。如图3所示。

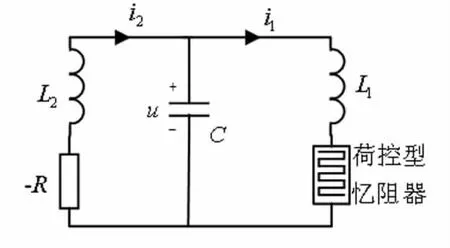
图3 标准蔡氏忆阻器电路

列出图示电路的状态方程，共有四个状态变量:

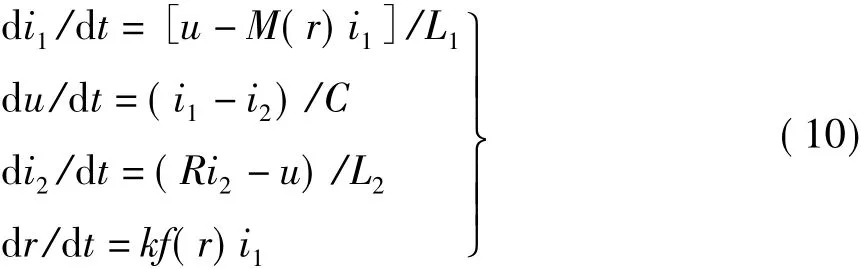
其中，M(r)=rRon+(1－r)Roff，窗函数 f(r)=1－(2r－1)2p。

我们做变换使 x=i1，y=u，z=i2，e=r，令 a=L2/L1，b=1/C，c=1/L2，R/L2=1，k=2.5，M(e)=M(r)=0.025e+10(1－e)，可得到其无量纲方程:

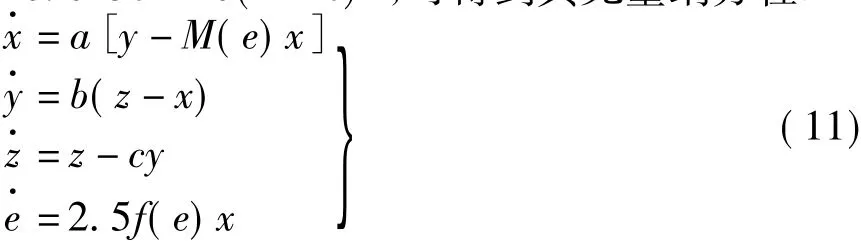
取 a=2.7，b=3.6，c=0.79，初始条件为 x=0，y=0.05，z=0，e=0.3。代入 Matlab 中进行仿真，得到的相空间或相平面上的投影如图4所示。

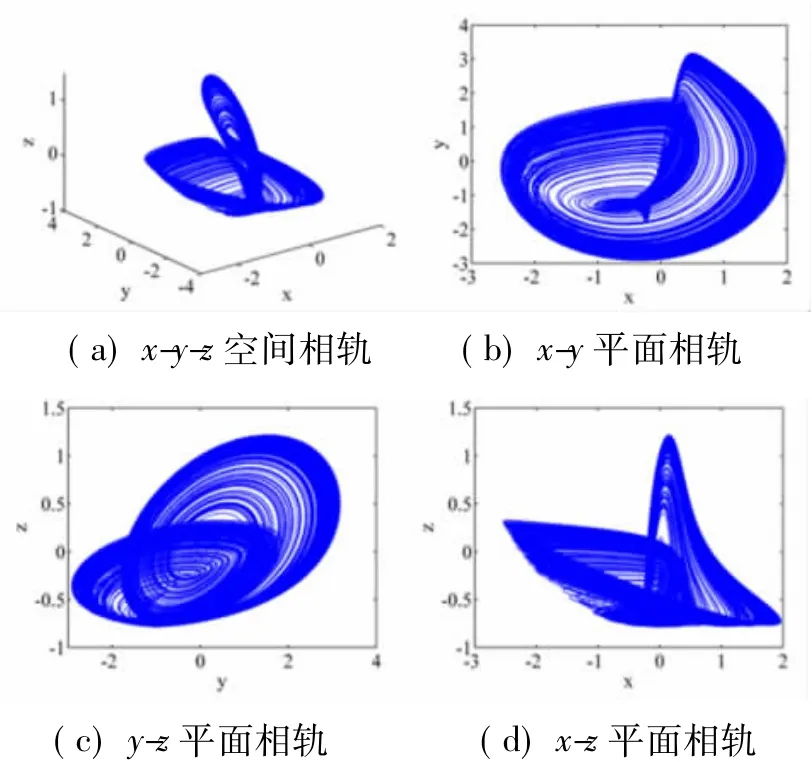
图4 混沌吸引子的投影

因方程为刚性的，最好用ode15s或ode23s而不宜用ode45算法，否则所用时间较长。Lyapunov指数分别为 L1=0.172，L2=0.001，L3=-0.005，L4=12.46，Lyapunov维数 dL=3.01。状态变量 y的时域波形如图5(a)所示，其特性貌似随机非周期性。在y=0的截面上三维Poincaré映射轨线在z-e平面上的投影如图5(b)所示。从相轨图、Lyapunov指数和维数、Poincaré映像以及时域波形可以得出该电路是混沌电路。

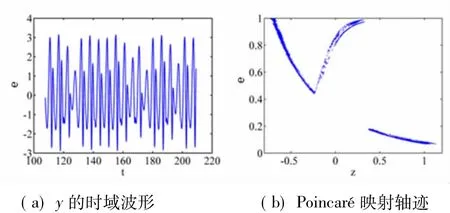
图5 状态变量y的时域波形和Poincaré映射

以b为变量的分岔图及Lyapunov指数谱如图6所示。此处画分岔图所选取的Poincaré截面y=0是一个在四维相空间中垂直于y轴过原点的平面，Lyapunov指数谱省略了L4。由图可知，分岔图和Lyapunov指数谱是基本一致的:当b＜4.7时，系统混沌;当b＞6.7时，系统收敛到一固定点;4.7＜b＜6.7时，最大Lyapunov指数时正时负，动力学行为比较复杂，在此不做研究。

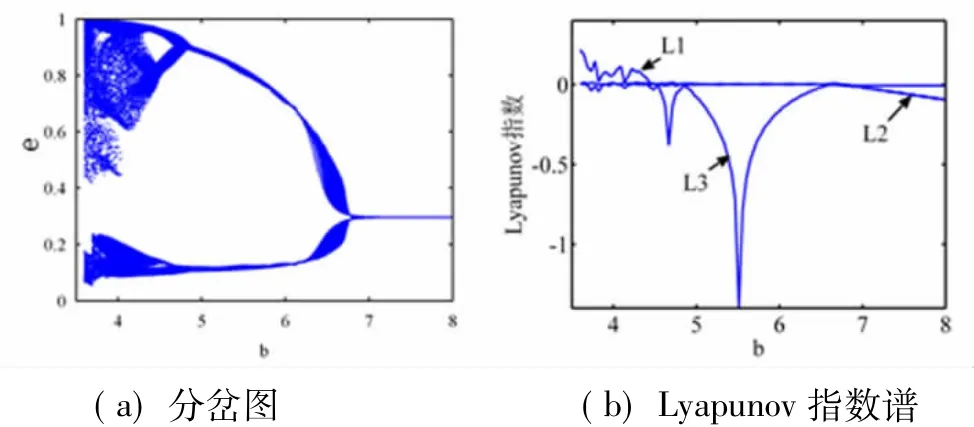
图6 参数b变化的分岔图和Lyapunov指数谱

该混沌系统的平衡点集为 A= {(x，y，z，e)|x=y=z=0，e=const}，即e坐标上的点集均是平衡点。由e的定义知，这里的c是一个0到1的常数，这与一般的混沌系统是不同的。当e=0.3时，有λ1，2=0.2379 ± j1.5297λ3=-18.3961，λ4=0，平衡点是不稳定的焦点;当 e=0.9 时，λ1，2=-0.9723 ±j3.0357，λ3=0.1839，λ4=0，平衡点是不稳定的鞍点;当 e=0.7 时，λ1，2=-0.1794 ± j1.3961，λ3=-6.7885，λ4=0，平衡点是稳定点。

所以，不同位置的平衡点有不同的稳定性。因此e在不同的初始值e时，其运行轨道会在混沌行为、周期行为或稳定的汇之间发生状态转移，在一定的电路参数下零特征值(λ4=0)对忆阻器混沌电路的稳定性也有很大影响。

3 忆阻混沌电路的Orcad仿真

忆阻器与二极管等非线性元件存在差异，忆阻器有记忆功能，而其他元件无此功能。例如，可通过伏安法测得二极管的伏安特性曲线，而忆阻器只要加正电压v+，电阻就会一直改变，从关状态经过一段时间约D2Roff/(2μvv+Ron)也会变为开状态。因此，不能用伏安法测忆阻器的伏安特性，而需要应用正弦电压扫描。

根据HP忆阻器的非线性掺杂漂移模型建立一个器件模型，可以在Orcad中像电阻一样使用。图7为用正弦交流电源供电时的滞后环图像，与HP实验室的结果相差不大，差异主要在于窗函数的构建。由图可见，当交流电压幅值为2V时，边界效应小，如图7(a)所示;当幅值为4V时，边界效应大，如图7(b)所示。

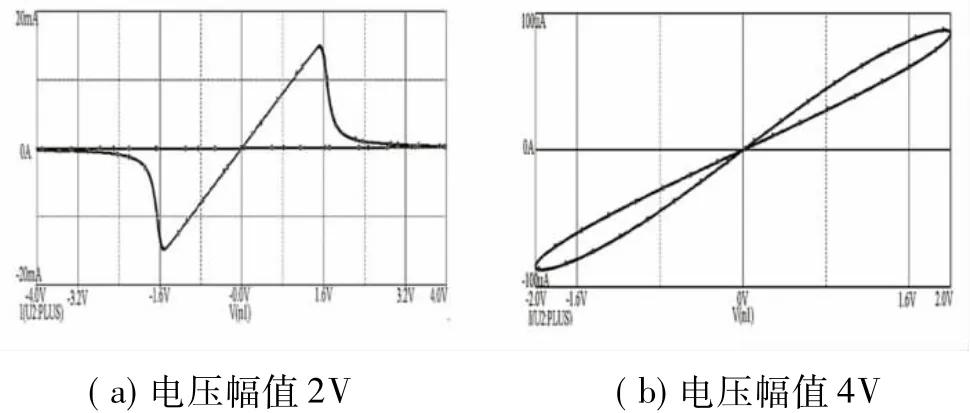
图7 忆阻器Orcad仿真结果

目前，忆阻器的Roff单位均为千欧级，而频率超过10Hz就不会有滞后环。图中Ron=0.1kΩ，Roff=40kΩ ，Rinit=28kΩ，p=1，f=1Hz，k=104s-1A-1。由于电路方程为刚性的，在Orcad仿真时要设置最大步长TMAX为1ms，相对精度Reltol为1E-6，否则得不到结果，这也说明了Orcad的数值仿真能力略逊于Matlab。

使用Orcad进行仿真，电感可以用回转器来等效替代，实现无内阻的电感，负电阻可用负电阻变换电路来实现。仿真电路如图8所示，此处用到的忆阻器中，Ron=0.025Ω，Roff=10Ω，Rinit=7Ω。仿真结果如9所示，其结果与Matlab仿真结果相同。

4 结语

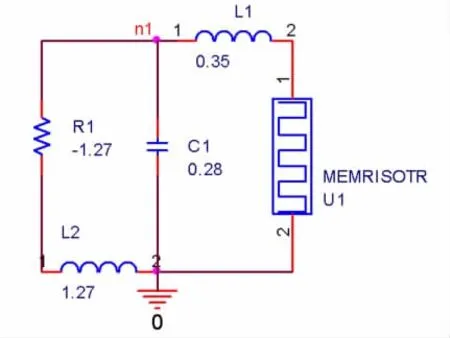
图8 Orcad仿真电路图

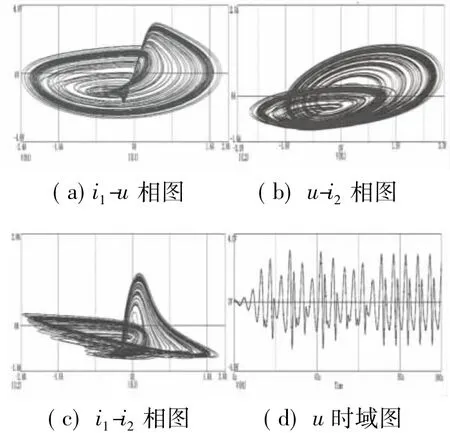
图9 忆阻器混沌电路的Orcad仿真结果

本文介绍了HP忆阻器非线性掺杂漂移特性，说明了HP忆阻器的独特性质。将HP忆阻器与蔡氏电路结合起来，构成了基于HP忆阻器的混沌电路。对忆阻器的Orcad模型进行了特性曲线的测试，与文献［2］中结果相同。混沌电路的Orcad仿真结果与Matlab结果相同。Matlab可以进行大量的数值计算，如计算Lyapunov指数等，而Orcad则可以设计电路元件参数。因此，要在不同场合使用不同软件，发挥其优势，使二者相辅相成。

［1］ L.O.Chua.Memristor-the missing circuit element［J］.IEEE Transaction on Circuit Theory，1971，18(5):507-519

［2］ D.B .Strukov，G.S.Snider，D.R.Stewart and R.S.Williams.The missing memristor found［J］.Naturre，2008，453:80-83

［3］ M.ltoh，L.O.Chua.Memristor Oscillators［J］.International Journal of Bifurcation and Chaos，2008，18(11):3183-3206

［4］ Y.N.JOGLEKAR，S.J.WOLF，The elusive memristor:properties of basic electrical circuits.European Journal of Physics，2009.30:661-675