解析底部剪力法计算多自由度体系水平地震力
2013-08-21冯继行
朱 泽 冯继行
(1.延安大学西安创新学院,陕西西安 710100; 2.烟台金建冶金科技有限公司,山东烟台 264670)
底部剪力法和振型分解反应谱法是计算多自由度弹性体系水平地震作用的两种最常用的计算方法[1],和振型分解反应谱法比较,底部剪力法不需要计算结构的各阶振型和频率,相对比较简单,因此,在求解多自由度弹性体系水平地震作用时应用比较广泛。但是,并非底部剪力法可以应用到所有结构,它有一定的适用范围和条件,《建筑抗震设计规范》[2]给出了适用范围:高度不超过40 m、以剪切变形为主,且质量和刚度沿高度分布比较均匀的结构,以及近似于单质点体系的结构。但是,目前学术界对底部剪力法的适用范围以及认识仍存在不同的误区和看法。因此,本文主要对底部剪力法的适用条件及范围逐一解析,以便能使大家对其有更深刻的理解。
1 底部剪力法的概念
多质点弹性体系在水平地震作用下任一时刻的结构底部剪力,可根据结构底部剪力相等的原则,将多质点弹性体系用一个与其基本周期相等的单质点弹性体系来代替,这样,根据地震作用及地震剪力的概念,就可以得出多质点弹性体系结构底部剪力的计算公式:

其中,α1为相应于多自由度弹性体系基本周期的水平地震影响系数;Geq为多自由度体系的等效总重力荷载,其取值方法为:

各质点的水平地震作用表达式为:

2 适用范围解析
按照式(1)和式(2)计算出结构底部剪力之后,采用式(3)求解各质点水平地震作用的前提是该多自由度弹性体系的地震反应应以基本振型为主,且基本振型应接近于倒三角形分布[1](如图1所示)。根据地震作用的概念可知,多自由度弹性体系各质点的水平地震作用与其水平相对位移直接相关,因此,为了简化计算,假定结构是以基本振型平动为主。同时,为了保证多自由度弹性体系的基本振型接近倒三角形,才规定结构高度一般不高于40 m,只有这样,才能保证结构以剪切变形为主,减少结构变形中的弯曲变形成分,避免基本振型曲线和倒三角形出入太大;质量和刚度沿高度方向均匀分布,则是保证多质点体系位移反应以基本振型为主,而基本振型通常是接近直线的,即基本振型接近于倒三角形分布,这样就可确定出各质点水平相对位移之比。由于各质点水平地震作用之和等于结构底部剪力,因此,可以据此算出各质点的水平地震作用,它与该质点的高度和质量成正比,这样本应按振型分配的水平地震作用就可以简化为按高度分配,也就是所谓的倒三角形分配。
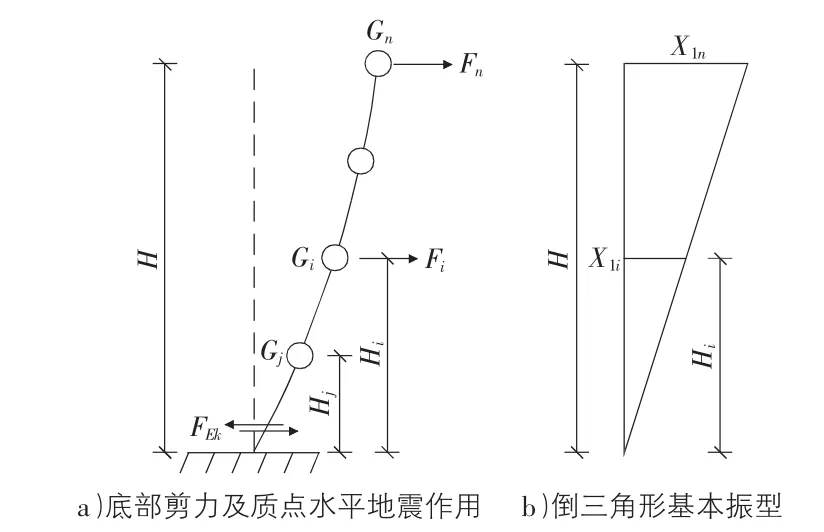
图1 底部剪力法
同时,当高度超过40 m,或者是结构自振周期较大(T1>1.4Tg)时,结构基本振型的弯曲变形成分将变大,且高振型的影响也不能忽视,使得按底部剪力法计算得出结构顶部的地震作用小于实际值,也就是说此时倒三角形顶部将包不住振型曲线,这种情况下可将结构总地震作用的一部分作为集中力作用于结构顶部,再将余下的部分按照倒三角形分配给各个质点,也就是所谓的顶部附加水平地震作用ΔFn(如图2所示)。
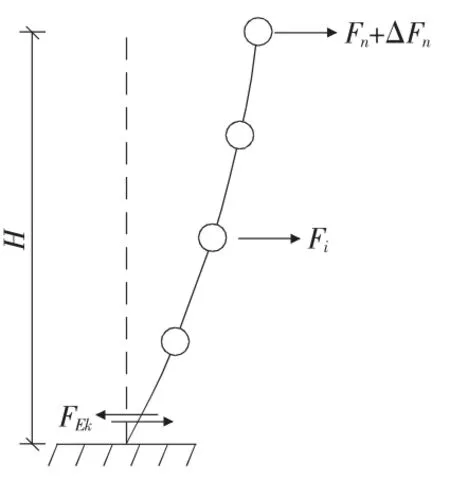
图2 顶点附加水平地震作用

因此,式(3)将变为:
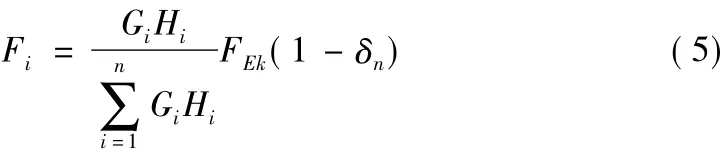
其中,δn为顶部附加地震作用系数。
3 结语
底部剪力法作为求解多自由度弹性体系水平地震作用的最简便方法之一,其适用条件及范围一直存在着误区,本文主要结合《建筑抗震设计规范》[2]对底部剪力法的使用条件及范围进行详细解析,以扫除大家对底部剪力法的盲区。
[1]丰定国,王社良.抗震结构设计[M].武汉:武汉理工大学出版社,2003.
[2]GB 50011-2010,建筑抗震设计规范[S].
