检测实验室质量控制结果评价方法

张卫民

（中国检验认证集团 广东有限公司黄埔分公司，广东 广州570100）

检测实验室的“产品”是检测结果，确保检测结果的公正、准确、可靠是检测实验室的最终质量目标，也是通过国家实验室认可、体系、计量认证评审的必要条件。 检测结果的质量控制是对检测过程进行监控， 以消除误差、 防止变化、 维持标准化作业的一个管理过程；ISO／IEC17025—2005《检测和校准实验室能力通用要求》中规定，实验室应有质量控制程序以监督检测的有效性。为控制实验室检测结果的准确性,实验室必须进行检测结果的质量控制。 本文作者一直从事实验室检测及质量控制方面的工作，当得到一系列的检测结果，结果是否有效可靠的？ 使用这些方法进行质量控制以及方法确认时，得到的结果怎么评价？ 评价方法有哪些？ 本文将重点探讨这方面的内容。

1 在重复性条件下测量结果的检查方法

1.1 两个初始测试结果

两个测试结果应在重复性限的条件下取得，测试结果之差的绝对值与重复性限r 比较；在正态分布的条件：

1.1.1 测试费用较低的情形

如果两个初始测试结果的绝对值不大于重复性限r， 测试结果可以接受，最终测量结果等于两个结果的平均值。 如果两个结果之差的绝对值大于r；则需要再做两个数据。若4 个数据的极差不大于临界极差CrR0.95(4)，取这4 个数据的平均值报告结果；如果4 个数据的极差大于临界CrR0.95(4)，取这4 个数据的中位数报告结果。 临界极差CrR0.95(4)=f（n）σr，其中f（n）为临界极差系数，其数据可查临界系数表。

1.1.2 测试费用高的情形

当测量费用较高，应再取一个测试结果。 若3 个结果的极差不大于临界极差CrR0.95(3)，取这3 个数据的平均值报告结果。 若3 个数据的极差大于临界极差CrR0.95(3)，并且不可能再取得第4 个测量结果，就取这3 个数据的中位数报告结果。

当有可能再取得第4 个测量结果时，实验室应取第4 个测量。 若4 个数据的极差不大于临界极差CrR0.95(4)，取这4 个数据的平均值报告结果。 如果4 个数据的极差大于临界极差CrR0.95(4)，取这4 个数据的中位数报告结果。

1.2 两个以上初始测试结果

当初始结果数大于2 的情形，在重复性条件下n＞2 时，确定最终测量结果的方法与n=2 的方法类似，在这里就不做详细讨论。

2 在再现性条件下所得结果可接受的检查方法

再现性条件是测量方法、测量设备、操作者以及环境设施等因素中有一项或几项不同的测量条件。

2.1 两个实验室测量结果一致性统计检验

2.1.1 每个实验室取得一个测量结果的检验

当两个实验室各取一个测量结果， 用再现性限R 检验两个结果之差的绝对值。如果差的绝对值不大于R，两个结果即为一致，取其平均值作为最终测量结果；如果两个结果之差的绝对值大于R，必须查明原因是否由于测量方法的精密度低和试样的差异所致。

2.1.2 每个实验室取得一个以上测量结果的检验

假设各实验室已取得了符合重复性要求的最终结果，只要考虑二个最终结果的可接受即可。

两个结果均为平均值，测量次数分别为n1,n2，两个结果之再现性临界差CrD0.95的表达式如下：

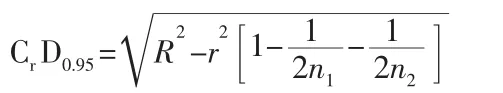
如果两个结果的差值的绝对值不大于再现性临界差CrD0.95，则认为两个实验室的最终测量结果是一致的，均可以接受，取两个结果的总平均值为最终测量结果；如果两个结果的差值的绝对值大于再现性临界差CrD0.95，则认为两个实验室的最终测量结果不一致，需查明原因。

上述方法在检测实验室日常的检测工作中会经常用到，只有掌握了上述方法，才能得出正确的结果，否则则容易出错。而对于质量控制及结果评价，如果只掌握上述方法是不够的，还必须涉及到下文要介绍F 检验和t 检验。

3 F 检验法（两组测量结果是否为等精密度的检验）

方差或标准偏差是反映测量精密度的重要标志，检验它的变化具有实际意义。方差分析又称变异数分析；也称为F 检验。它是英国统计学家R. A. Fisher 首先提出的一种统计方法。

F 检验的统计量是：

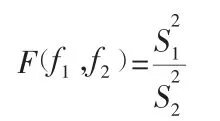
4 t 检验法（两组测量结果平均值差异显著性的检验）

4.1 t 分布的概率

1908 年，戈塞特在使用斯徒登(Student)的笔名发表的论文中提出了平均值的理论分布，引入了称为“斯徒登t”的概念；统计量t 值按下式计算：

4.2 t 检验的应用

任何显著性差异都是由平均值的差异引起的，用t 检验可以确定两个平均值之间是否由显著性差异；在进行t 检验之前先要进行F 检验，确定方差之间没有显著性差异才能进行t 检验。当统计量t 值不大于从t 分布表中查得临界值就可以判定两个平均值没有显著性差异；反之则判定有显著性差异。

4.2.1 平均值与标准值的比较（用于方法确认、质量控制等）

例1： 实验室制定了一个快速测定铁矿石中含硫量的新方法，用铁矿中含硫量为0.123%标准样品来确认该方法。4 次测定结果分别为0.112%，0.118%，0.115%，0.119%， 试问测定结果是否在置信范围之内，新方法是否可以通过确认？

题解：测定结果的平均值和标准偏差按下式计算：

因为测定值0.116%低于0.123%，要判定这是否在随机影响的限度以内，要利用单尾t 值表，如果使用5%显著性水平作为判别标准，自由度为3，查t 分布单侧临界值表得t0.05,3=2.35，现在t=4.375＞t0.05,3=2.35，这说明不完全是随机影响所致，一定还有系统影响存在，方法不能通过确认。

实际上，纵观近几年的邮品拍卖，只要是精品、珍品，就能引起买家的追逐，不仅成交相当活跃，而且市场潜力十分可观。如被称为我国“十大珍邮”之一的“全国山河一片红”邮票，单枚价格的涨势就十分惊人：早在1977年，就有150元一枚的身价；1987年，它的身价又涨至800元；到了1993年，成交价为3万元；在1997年，北京的一场艺术品拍卖会上，一枚的成交价高达17万元。2000年广州国际邮票钱币博览会上，一枚《全国山河一片红》邮票更是卖到18．5万元。据业内人士介绍，该邮票在拍卖场上，只要一亮相就深受藏家追捧，几乎没有流拍的事情发生。由此可见，只要投资者收藏有重大纪念事件方面的邮票，增值的可能性很大。

4.2.2 两组测量平均值的比较（用于质量监控，如人员或方法的比对或留样再检测的二次结果可接受的判定）

在实验室质量控制中，通常要进行方法比对、人员比对、仪器比对、留样复检和实验室间比对等活动，所得的平均值一般是不相等的。在此情况下，尽管待比较的两个平均值中的任何一个都不能视为标准值或真值。 但仍然可以用t 检验确定两个平均值是否由显著性差异。

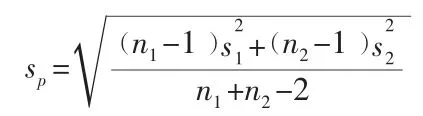
其自由度为f=n1+n2-2

例2：某个实验室为实施质量监控计划，对于葡萄酒中乙醇含量的测试项目（属于测试费用较低的情形），在相同条件下（即方法、设备、环境等试验条件相同）进行人员比对。分析人员甲开始进行了三次测试，其结果分别是12.16%、12.62%、13.05%，而分析人员乙开始进行了二次测试，其结果分别是13.16%、12.10%，已知标准方法通过精密度试验给出的重复性标准差是σr=0.26%， 再线性标准差是σR=0.38%，根据上述所介绍的测量结果可接受性及统计检验方法，试问人员比对测试应该如何进行下去？ 最后的比对结果二人各为多少？ 二人的测试结果有无显著性差异？

这是分析人员甲的最终测试结果，其标差为S=0.4035%。

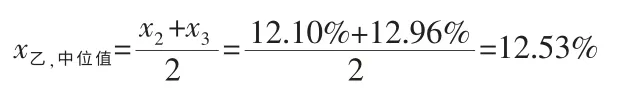
这就是分析人员乙的最终测试结果，其标差为S=0.6228%。

在人员比对中，要判断二人的结果是否可以接受，或存在显著差异，可采用t 检验法进行判定，但在t 检验前必须运用F 检验法判定两人的测试是否是等精密度测量。

两组测量的合并标准偏差sp按下式计算：

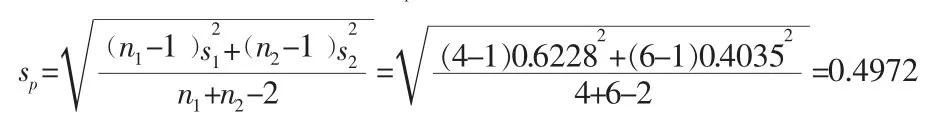
按下式计算统计量并进行t 检验：

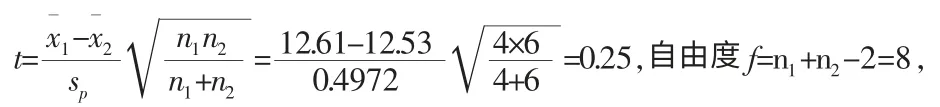
在选择显著性水平为5%， 查t 分布双侧临界值表得t0.05,8=2.26＞t=0.25，这表明两个人员的最终测试结果是一致的，均可以接受，取两个结果的总体平均值为最终结果。

5 结束语

上述的判定方法，不仅可用于质量监控的人员比对中，也运用于方法比对、设备比对、两个实验室间的比对及留样再检测的二次结果的比对等质量监控活动中。

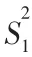
可见，在检测或方法确认中必须掌握统计假设检验技术，对质量监控（各种比对试验的可接受性）及实验检测结果的评价作出科学、准确、严密的判定。

［1］郑亚玲.浅谈实验室内的质量控制[J].现代测量与实验室管理，2010(04).

［2］翟建才，翟羽，蒋洪，马显光.测量不确定度的评价和实验室质量控制[J].现代科学仪器，2007(02).

［3］ISO／IEC17025-2005 检测和校准实验室能力通用要求[S].

［4］谭和平，陈能武，张云嫦.化学实验室认证认可与质量控制[J].中国测试，2010(5).

［5］CNAS-CL10:2012，检测和校准实验室能力认可准则在化学检测领域的应用说明[S].