合成孔径雷达成像自聚焦算法的比较

周学军 韩香娥

(1.西安电子科技大学 理学院，陕西 西安710071；2.延安大学 信息学院，陕西 延安716000)

0 引言

假设g∈CM×N是完全聚焦的SAR 图像，距离压缩后(在距离方向的一维DFT), 采集傅立叶成像数据G∈CM×N与g∈CM×N通过施加到每个列的一维DFT 联系：

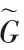
在φe(k)∈[-π，π)M是一个一维傅立叶相位误差函数。 利用（1）和（2），失焦图像与完全聚焦图像，通过（3）联系起来。

聚焦算法形成一个估计φe的相位误差函数进行修正散焦的影像数据以恢复图像。

SAR 自聚焦算法的任务是首先要对经过处理后的未补偿的SAR信号进行相位误差估计，然后消除其相位误差。 SAR 自聚焦算法就其本质而言是一个二维估计问题，在公式（2）中的相位误差既是空变的又是不可分离的乘性噪声的事实使问题变得极为棘手。影响成像的几何线性，分辨率、图像对比度和信噪比的主要因素取决于相位误差的性质和大小，基于处理孔径上相位误差形式，表1 给出两大类相位误差及其每一类对SAR 成像的一般影响。

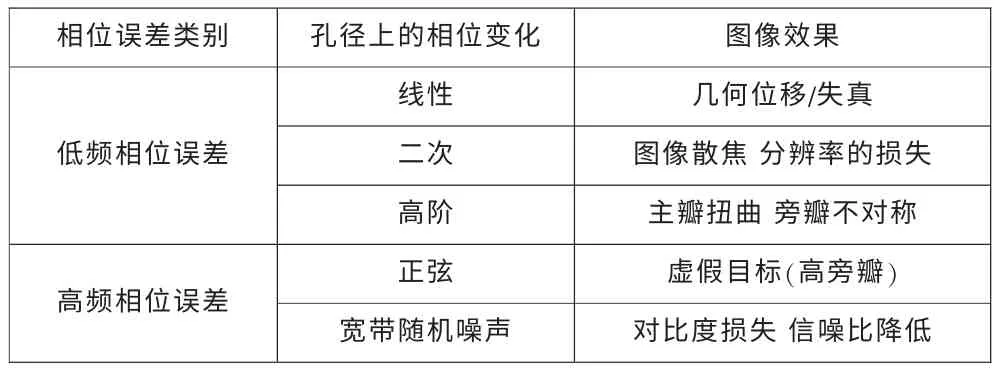
表1 相位误差的分类

1 几种实用的自聚焦算法的比较

一般来说，自聚焦算法可以划分为两类：基于模式算法和非参数算法。 基于模式的自聚焦算法估计相位误差的模式展开系数。 低阶模自聚焦仅能估计二阶相位误差，而更复杂的方法还可以估计高阶多项式相位误差。 子孔径相关法（MD）和多孔经相关法（MAM）是针对低频相位误差补偿提出的基模自聚焦算法的范例。基于模式算法虽然执行起来相对简单而且算法高效。不过只能相位误差被正确估计的情况下才能保证这样的优越性。

第二类自聚焦算法，即非参数自聚焦算法，典型的有相位梯度自聚焦算法，基于最小熵准则和最大对比度准则的自聚焦方法，这些方法都不需要相位误差的先验知识。 特别地，相位梯度自聚焦算法几种改进的算法。 其中特征向量法是在PGA 框架下运用了极大似然算子取代了原始的相位差算子核，改进的相位梯度自聚焦算法的策略通过选择一组高质量的目标以提供非迭代的PGA 解。 另一种方法是运用加权最小二乘法以实现相位误差最小化的PGA。 适用范围扩大，计算高效。

在一些SAR 应用中，相位误差显著依赖位置，空变的自聚焦的常用的方法是将大场景分成更小的子图像，每个子图像的误差近似不变的，因此，传统的空间不变的自聚焦程序可以应用到每个子图像。当重新聚焦时，个别的子图像拼接或镶嵌在一起产生完整的场景图像聚焦图像。

2 性能评价标准

第一个测试是检查在方位域一维的点目标响应。聚焦质量质量指标包括3dB 的分辨率，信噪比，峰值旁瓣电平，相位估计的均方误差，熵。 在第二个是二维测试性能评价标准包括图像熵和Fisher 信息。

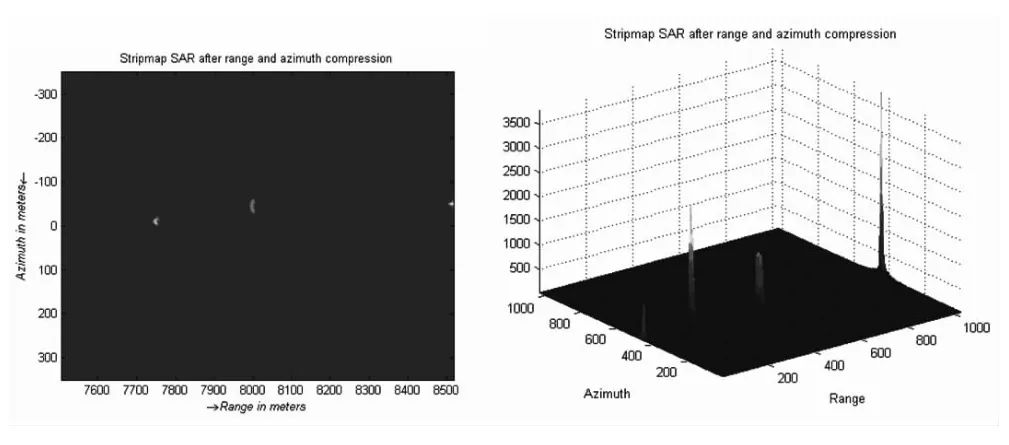
3 点目标仿真实验

模拟沿X 轴正方向水平运动的SAR 平台速度V=200m/s， 高度H=10000m， 天线方位向孔径长度D=2m 发射chirp 信号载波频率fc=2GHz，持续时间Tr=0.5ns，调频带宽Br=30MHz，目标个数Ntarget=3；目标位置矩阵: 格式[x 坐标,y 坐标,目标散射系数]。

方法上先对点目标成像进行距离压缩，然后在频谱域内乘上不同形式的随机相位噪声，用距离-多普勒算法方位向压缩成像，采用不同的自聚焦方式实现对相位误差的去除，最后根据性能指标比较。

4 结论

基于模型算法如子孔径相关算法和多孔径相关算法在低阶相位误差估计方面计算效率高。 非参数方法如PGA、EV 和WLS 是估计其他各种相位误差上优于前者。 总之，3dB 分辨率和信噪比是评价在低阶相位误差存在的点目标响应的好的聚焦质量指标，而旁瓣峰值标准是最适合高频率的相位噪声估计。 图像熵能很好地衡量图像聚焦。 但相位误差均方值一般能不显示图像质量。

［1］张澄波.综合孔径雷达原理、系统分析与应用[M].科学出版社，1989.

［2］郭华东，等.雷达对地观测理论与应用[M].北京:科学出版社，2000.

［3］D.A.Ausherman,A.Kozma,J.K.walker,H.M.JonesandE.e.Poggi.nevel pments in Radar Imagimg,IEEE Transaetionson Aeros Paeeand Eleetronie Sys 七ems[J].1944,20(4)：363－400.

［4］禹卫东.合成孔径雷达信号处理研究[D].南京航空航天大学，1997，9.