基于空间调制和单元器件的短波红外光谱探测

王亚南，马彦鹏，亓洪兴，况耀武，舒 嵘

(中国科学院上海技术物理研究所，上海200083)

1 引言

由于很多物质在1～2.5 μm波段具有独特的光谱特性，所以短波红外探测器被广泛应用于空间对地探测中，如了解资源分布、土壤水分监测、大气成分分析、农作物估产等各个方面［1－2］。

目前广泛研究的光谱探测主要利用线阵探测器直接获取光谱信息。由于当前的短波红外焦平面探测器性能的限制，利用线阵器件的短波红外探测器很难实现较高信噪比并且难以克服响应不均匀的缺点［3］，除此之外，线列的短波器件价格昂贵也是制约该种光谱仪应用于实际生产生活的重要原因。

使用单元探测器和调制模板的方法［4］在有效避免不均匀性的影响和提高信噪比的同时可以大幅度地减少系统的造价。在文献［5］中对这种多通道光谱探测方法做了详尽的理论推导和论述，但作者只是给出了理论上的证明。本文在此基础上进行了实验，验证了用DMD作为空间光调制模板，将基于Hadamard变换的多通道探测技术应用于短波红外探测上的可行性。

2 多通道光谱探测基本原理

多通道光谱探测是相对于单通道光谱探测而言的。图1是单通道探测的基本原理:入射光通过狭缝，经分光元件分光之后入射到一个线阵探测器，线阵探测器的每个元对应的是光谱面的不同的谱段，所以如果采用单通道探测的方法，探测n个谱段的光谱信息就需要n元的线阵探测器。

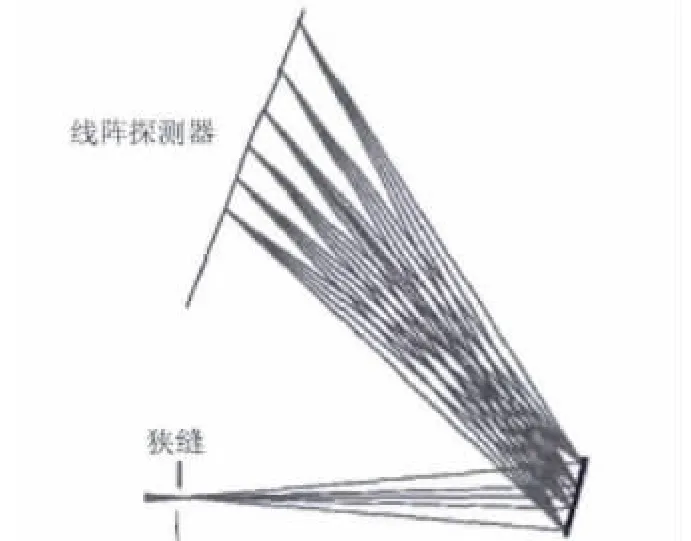
图1 单通道探测原理Fig.1 Single-channel detection principle

与单通道探测方法不同，如图2所示，多通道光谱探测不直接获取光谱面各个谱段的强度信息，而是在光谱面进行调制，将各个谱段叠加之后的信息用单元探测器进行探测之后再由数据处理软件还原出各谱段的原始强度信息。利用该种光谱探测的方法，相对于单通道探测，可以获得更高的信噪比。图3是4通道基于Hadamard变换的光谱探测［6］原理图:假设每次测量引入的误差都是随机的，并且相互独立。

使用单通道测量方法时，对每个光谱分量进行测量都会引入一个误差值:

而在使用多通道测量方法进行测量时，进行四次测量，每次测量的都是不同光谱分量的组合，根据理论分析可以得到:

其中，ηi为探测器读数;φi为实际个谱段的强度;ei是每次测量引入的误差值;σ2为均方误差。

比较式(1)和式(2)明显可以看出多通道光谱探测的方法具有更小的误差。实际上，采用S矩阵在光谱面进行调制时，相对于单通道探测的方法具有如下信噪比优势:

其中，N为调制矩阵的阶数;SNRMutiple为多通道探测的信噪比;SNRSingle为单通道探测的信噪比。此式的证明比较繁琐，详细证明过程可以参照参考文献［6］。

除了具有明显的信噪比优势之外，相对于单通道探测方法，多通道光谱探测还具有以下优点:①由于在多通道探测方法中使用单元探测器而非具有空间分辨率的线阵探测器，所以可以完全消除探测器本身的非均匀性带来的误差;②采用多通道光谱探测的方法，每次探测的都是多个谱段分量的叠加，当光谱分辨率提高时，信噪比并不会明显下降;③采用单元探测器使得多通道光谱探测在实用方面具有明显的价格优势。

3 系统设计

系统包含光学和电子学两大部分，其中光学部分包括空间光调制器、单元探测器和其他光学部件，电子学部分主要包括数据采集单元和控制电路及软件。系统各部件及参数如表1所示。

表1 系统各部分结构及参数Tab．1 System structure and parameters

作为整个系统的核心部件，光调制器的编码准确度会直接影响最终数据反演的结果，所以空间光调制器的选用尤为重要。

本文采用的编码矩阵是只由元素0和1组成的S矩阵，要求空间光调制器在进行光谱面的调制时具有良好的开关特性，即能够对入射的各光谱成分做到完全的透射和完全的不透射。

本文选用TI公司的DMD器件作为系统的光调制器。DMD(Digital Micromirror Device)，即数字微镜器件［6］。一片DMD实际是由成千上万个倾斜的显微的、铝合金镜片组合，当微镜处于不同的翻转状态时就会将入射光向不同方向反射，如果向+12°方向反射的光被探测器接收，则向－12°方向反射的光被舍弃。

除了具有良好的开关特性之外，DMD器件还具有以下优点，使其成为本系统核心部件—空间光调制器的最佳选择:①DMD器件的玻璃窗口可以透过短波红外光;②每片微镜的尺寸为13.6 um，与短波红外波长差距明显，用于短波红外的探测时不会产生衍射;③目前使用的DMD器件的帧频为200 Hz，完成编码所用时间较短，可以有效减少外界光变化对系统产生的影响。

系统的光学结构如图4所示。入射光通过狭缝之后经过分光装置后照射到DMD上，DMD对光谱面进行调制，调制后的光经会聚镜会聚后照射在单元探测器上，此时单元探测器收集的总的光强信息，称之为原始数据，之后利用原始数据和调制矩阵反演出各个谱段的强度信息。随时间变化的光强信息(原始数据);Ⅲ利用原始数据和调制矩阵信息解算光点位置信息;Ⅳ移动激光光点并重复Ⅱ、Ⅲ。

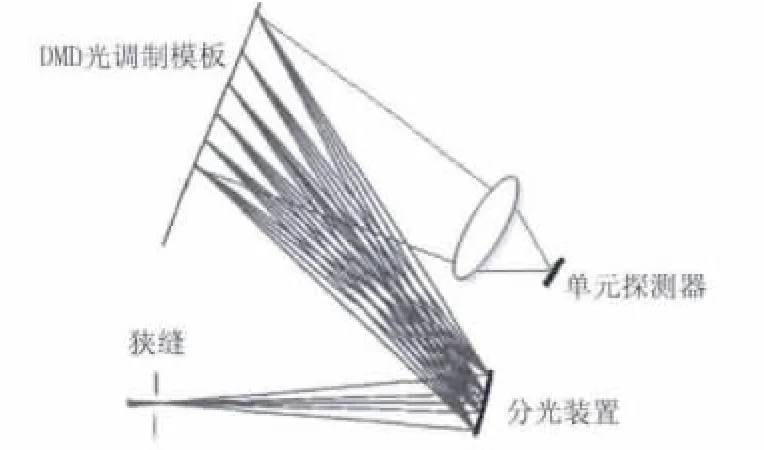
图4 系统光学结构图Fig.4 Optical structure

本文共进行了三次实验，分别是调制矩阵为251阶，511阶和1023阶时的光点移动实验。随着调制矩阵阶数的增加，探测器收集到的原始数据量增多，同时分辨率也随之增加。

实验装置的结构如图5所示。

4 实验方法与结果

实验采用激光光点来模拟光谱中的单色光成分，用激光光点的位置变化来模拟光谱分布的变化:激光光点处于不同的位置相当于不同的光谱成分入射。

实验步骤如下:Ⅰ固定激光光点位置;Ⅱ向DMD发送调制矩阵同时获取由单元探测器收集的

原始数据反映的是经过调制矩阵调制的总光强信息，实际上原始数据的每个点都对应一幅调制信息中的元素1所占的比例。当调制信息不断变化时，原始数据会呈现一个规律的变化，这个规律实际上也是调制矩阵每行元素的变换规律。对比图6(a)，图7(a)，图8(a)可以看到，随着调制矩阵阶数的增加，曲线形状都会呈现与矩阵相关的规律性变化，但是数据量会明显增多。

系统的分辨率是由原始数据量所决定的，即是由调制矩阵的阶数所决定的。分辨率和调制矩阵阶数之间满足关系式:

其中，R为距离分辨率;L为调制矩阵在DMD上的条带宽度;a为微镜的边长;b为微镜的间距;n为条带横向包含的微镜的个数。其中n和调制矩阵阶数N的乘积应为小于1024的最大正整数。因为微镜的间距很小，所以b的值可以忽略不计。根据式(3)，当矩阵阶数分别为251、511和1023时，系统的分辨率如下表所示。

表2 调制矩阵阶数N与分辨率对应关系Tab．2 Correspondence between N(order of modulation matrix)and resolution

对比图6～8各图中图(b)的实验结果的可以发现随着调制矩阵阶数的增多，系统还原出的光点光强分布包络更加平滑，从侧面反映了位置分辨率的提高。总之，实验结果充分表明了基于Hadamard变换，利用空间光调制器，仅使用单元探测器获取多个谱段的信息是可行的。

5 总结

本文利用空间光调制器和单元探测器，基于Hadamard变换，用单点位移的方法模拟了单像元多谱段信息的获取，取得了良好的实验结果，在目前国内焦平面器件发展不成熟和进口焦平面器件造价较高的情况下，为短波红外光谱仪的制备提供了一条新的思路。

［1］ Lin Wuwen，Xu Jin，XShilu．Development trent of IR detection technology［J］．Laser ＆ Infrared，2006，36(9):840 －843．(in Chinese)林武文，徐锦，徐世录．红外探测技术的发展［J］．激光与红外，2006，36(9):840 －843．

［2］ Ren Bin．Shortwave infrared imaging spectrometer electronics key technology research［D］．Xi'an:Xi'an institute of optics and precision mechanics of CAS，2009:1 － 30．(in Chinese)任斌．短波红外成像光谱仪电子学关键技术研究［D］．西安:中国科学院西安光学精密机械研究所，2009:1－30．

［3］ Cao Yang，Jin Weiqi，Wang Xia，et al．Development in shortwave infrared focal plane array and application［J］．Infrared Technology，2009，31(2):63 －68．(in Chinese)曹扬，金伟其，王霞，等．短波红外焦平面探测器及其应用进展［J］．红外技术，2009，31(2):63－68．

［4］ Ye Hunian，Ye Mei，Yang Lixin．Hadamard transform optical imaging［M］．Wuhan:Huazhong University of Science and Technology press，2012．(in Chinese)叶虎年，叶梅，杨新立．阿达玛变换光学成像［M］．武汉:华中科技大学出版社，2012．

［5］ Qi Hongxing，Chen Muwang．Study on Hadamard transform near-infrared imaging spectrometer［J］．Infrared Technology，2005，27(6):463 －468．(in Chinese)亓洪兴，陈木旺．短波红外Hadamard变换高光谱成像技术研究［J］．红外技术，2005，27(6):463 －468．

［6］ M Harwit，Neil J A Sloane．Hadamard transform optics［M］．New York:Academic Press，1979:1 －104．