相位式激光测距的FFT与apFFT鉴相研究
2013-08-17刘恩海
陈 栋,刘恩海
(1.中国科学院光电技术研究所,四川成都610290;2.中国科学院大学,北京100039)
1 引言
相位式激光测距作为一种高精度、非接触的测量方式,在大地大气探测、空间位置高精度测量等领域起着很重要的作用。其基本原理为:通过测量调幅连续波发射光束和反射光束的相位差来测量时间间隔,进而求出测量距离[1]。假设光速为c,调制频率为 f,相位差为 Δθ,则测量距离为 d=cΔθ/(4πf),可看出鉴相精度影响测距精度[2]。为实现亚毫米精度的相位式激光测距,选取一种高速、高精度的鉴相方法具有重大的现实意义。总体上,常用的鉴相方法可分为模拟法和数字法两种,模拟法有着电路复杂、元器件要求高、精度差等缺点;而数字法具有成本低、适应性好、测量精度高等优点[3]。数字法主要包括自动数字鉴相法、数字相关法和FFT法。由于被测距离的远近不同,回波幅度差别很大,采用自动数字鉴相法会产生很大的测量误差[4]。数字相关法和FFT法运算量小,都能有效抑制高斯白噪声 ,但数字相关法的反余弦运算限制了其鉴相范围为0~π。文献[6]提出一种apFFT法,并证明该方法相比FFT法具有抑制频谱泄漏的特性,文献[7]证明apFFT法具有“相位不变性”,即在非同步采样的情况下,无需附加校正措施即可准确鉴相。现有文献在对比FFT与apFFT的鉴相性能时未考虑两者使用的采样点数问题,而在相位式激光测距中考虑鉴相使用的采样点数具有实际的工程意义。本文对FFT和apFFT进行理论研究和仿真实验,对比两者在高斯白噪声和频率偏移影响下的鉴相性能,并考虑采样点数的问题,根据实验结果选择适用于亚毫米精度相位式激光测距的鉴相方法。
2 FFT与apFFT的理论研究
2.1 FFT法的原理和偏差
FFT法通过对参考信号和测量信号的采样数据分别做FFT,找到各自的主谱线,再以两者主谱线对应相位的差值作为相位式激光测距的相位差[8]。对于频率为f的余弦信号,其频谱应该是在±f处的线谱,但在使用FFT鉴相时先对信号进行采样和截短,由于截短时使用的窗函数在频域内不是理想的冲击函数,导致信号的频谱不只在±f处有谱线,而且在以±f为中心的频带范围内都出现谱线,即产生频谱泄露。文献[9]证明,对余弦信号x(t)=Acos(2πft+φ)(其中A为幅度,φ为相位)进行同步采样,即采样频率fs和采样数据长度N满足以下条件:(1)fs=mf,m为大于2的正整数,即采样频率是信号频率的整数倍;(2)N是m的整数倍,即采样数据包括一个或多个整周期。那么,使用这N点数据做FFT时,所得的频谱无泄漏。在相位式激光测距中,由于频率源存在一定的频率偏移,无法满足上述条件,所以使用FFT进行鉴相时会由于频谱泄露带来偏差。对FFT在相位式激光测距中的鉴相偏差进行分析:
设参考信号为 x1(t)=A1cos(2πft+φ1),测量信号为 x2(t)=A2cos(2πft+φ2)(其中 A1、A2为幅度,φ1、φ2为相位)。以 fs对两信号采样,采样数据长度为N,则x1(t)对应的离散序列为:

按欧拉公式展开:

则主谱线K=[Nf/fs],括号表示四舍五入取整。设归一化频率偏移 δ=Nf/fs- K,|δ≤0.5|,x1(n)的正频率复信号和负频率复信号在K处的DFT结果分别为:

将X11(K)和X12(K)进行矢量相加得到X1(K),即为x1(n)在K处的DFT结果。因为在相位式激光测距中进行的是同步采样,有|δ|1,当1≤K≤N/2-1时有|X11(K)||X22|X22(K)|,故矢量相加得到X1(K)的相位可以表示为:

同理可得X2(K)的相位可以表示为:
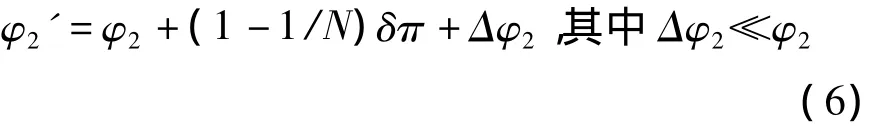
则使用FFT法测得相位差为:

由以上推导可知:由于实际系统存在频率偏移,FFT法会发生频谱泄露,从而引起鉴相偏差。但是在相位式激光测距中,需求的是参考信号与测量信号的相位差,在作差过程中两者鉴相偏差的(1-1/N)δπ部分得以抵消,所以FFT法用于相位式激光测距中仍有很高的鉴相准确度。
2.2 apFFT法的原理
apFFT法以其“相位不变性”、频谱泄露抑制能力好等优点迅速应用到相位式激光测距中[6-7],apFFT 法先对采样数据进行全相位预处理,对预处理的结果进行FFT,然后求出主谱线对应的相位作为鉴相结果。双窗全相位预处理的过程为:对于长度为2L-1,中心样点为s(0)的数据序列 s(n)=[s(L-1),…,s(0),…,s(-L+1)],将L阶对称窗函数W1和W2卷积得到加权窗函数W=W1*W2,使用W对s(n)进行加权,得到s(n)'=W×s(n)。将s(n)'从第一个数开始每隔L个数两两相加,得到长为L的序列s(n)″,s(n)″即为全相位预处理的结果。当L=3时,apFFT法的等效框图如图1所示。

3 计算机仿真分析
为对比 FFT法和 apFFT法的鉴相性能,在MATLAB中设计仿真方案。设参考信号的信噪比为60 dB,相位为30°,测量信号的相位为60°,调制频率为50 MHz,使用差频鉴相技术混频至20 KHz进行测量,采样频率为1.28 MHz,即每个周期同步采样64点。FFT使用的采样点数分别为64点和128点,apFFT使用的采样点数为127点,经全相位预处理后进行的是64点FFT。
3.1 频率偏移影响下的鉴相性能
设归一化频率偏移量 δ∈[-0.1,0.1],每隔0.01变化一次,在每个归一化频移量下做10000次蒙特卡洛仿真,鉴相偏差与归一化频移量的关系如图2所示。

图2 频移下的鉴相偏差对比Fig.2 Deviation comparison with frequency deviation
由图2可知:频率偏移使FFT出现鉴相偏差,鉴相偏差随着归一化频率偏移量的增大而增大;而apFFT能够很好地抑制频率偏移的影响,鉴相结果仍旧准确。由δ=Nf/fs-K可知:当归一化频率偏移量δ一定时,采样点数N越小,则频率偏移量Δf越大,故64点FFT的鉴相偏差曲线总在128点FFT的上方。
3.2 高斯白噪声影响下的鉴相性能
设测量信号的信噪比在20~55 dB每隔1 dB变化一次,在每个信噪比下做10000次蒙特卡罗仿真,FFT与apFFT的鉴相性能如图3所示。

图3 不同信噪比下的鉴相性能对比Fig.3 Performance comparison with different SNR
由图3可知:鉴相准确度从高到低为:128点FFT、127点 apFFT、64点 apFFT。在只有高斯白噪声影响的情况下,FFT使用的采样点数越多,鉴相越准确;在采样点数相同时,FFT比apFFT鉴相更准确,且随着信噪比降低,两者鉴相准确度相差得也越多;FFT与apFFT均对高斯白噪声有很好的抑制作用,当信噪比高于45 dB时,64点FFT、128点 FFT与127点apFFT的鉴相标准误差均小于0.04°,在50 MHz调制频率下对应的测距标准误差小于0.34 mm。
3.3 白噪声和频移共同影响下的鉴相性能
由上述分析可知:在采样点数相同的情况下,当仅存在高斯白噪声的影响时,FFT比apFFT鉴相准确;当仅存在频率偏移的影响时,FFT会发生频谱泄漏而引起偏差。故下面对比在高斯白噪声和频率偏移共同影响下FFT和apFFT的鉴相性能。设测量信号的信噪比为25 dB,归一化频移量δ∈[-0.1,0.1],每隔0.005变化一次,在每个归一化频移量下做10000次蒙特卡洛仿真,在高斯白噪声和频移共同影响下的鉴相标准误差曲线如图4所示。

图4 白噪声和频移共同影响下的鉴相标准误差Fig.4 Standard error comparison with white noiseand frequency deviation
由图4可知:在采样点数相同,高斯白噪声信噪比25 dB的情况下,当归一化频率偏移量较小时(δ∈[-0.035,0.045]),FFT 比 apFFT 鉴相准确,且随着频率偏移的进一步减小,两者鉴相准确度相差越多;当归一化频率偏移量较大时,apFFT比FFT鉴相准确,且随着频率偏移的进一步增大,两者鉴相准确度相差越多;若FFT使用的采样点数减半,则其鉴相的标准误差总是大于apFFT。
在实际系统中,频率源使用的晶振的稳定度达到1 ppm,即128点FFT对应的归一化频移量最大值仅为2×10-6,故为得到更高的鉴相准确度,应选用FFT作为鉴相方法。在50MHz的调整频率下,若要求测距标准误差低于1 mm,则鉴相标准误差应小于0.12°。
设测量信号信噪比为35 dB,归一化频率偏移量为0.02,在此条件下每采样128点做FFT进行一次鉴相,每采样127点做apFFT进行一次鉴相,重复10000次,其中FFT的测量结果如图5所示。
由图5可知:FFT鉴相结果近似成正态分布,均值为30.0073°,标准误差为0.0908°,在50MHz调整频率下对应测距标准误差为0.76mm,而apFFT的鉴相标准误差为0.1045°,鉴相准确度低于FFT。实际中相位式激光测距系统的信噪比更高,频率偏移更小,使用FFT鉴相能够达到更高的准确度。

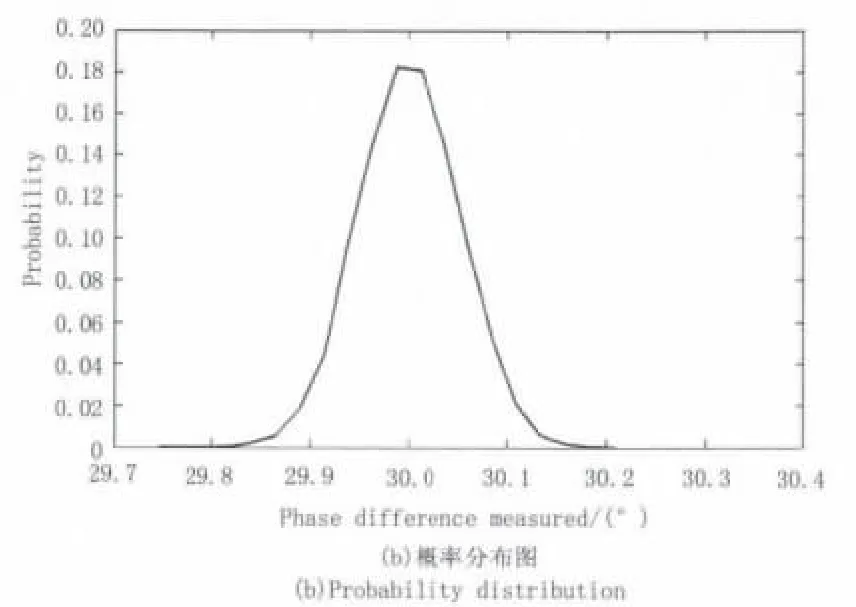
图5 FFT鉴相结果Fig.5 Results of phase discrimination using FFT
4 结束语
文中通过对FFT法和apFFT法进行理论分析和仿真实验,对比了两者在高斯白噪声和频率偏移的影响下的鉴相性能,并考虑两者使用的采样点数。仿真结果表明:在使用采样点数相同的情况下,当只存在高斯白噪声的影响时,FFT比apFFT鉴相准确;当只存在频率偏移的影响时,FFT会出现鉴相偏差;当存在白噪声和频率偏移共同影响时,在归一化频移量较小的情况下(25dB时对应 δ∈[-0.035,0.045]),FFT比apFFT鉴相准确,故结合实际系统的频率偏移很小的具体情况,为得到更高的鉴相准确度,应该选用 FFT作为鉴相方法。在信噪比35dB、归一化频移量0.02的情况下使用128点FFT(即测距速率10KHz)的鉴相标准误差为0.0908,在调整频率50MHz下对应的测距标准误差小于1mm。综上所述,FFT适合用于文中研究的相位式激光测距的相位差测量,文中的研究为下一步实际系统的研制奠定了基础。
[1] Zhang Ting,Zhang Keshu.Study of phase-shift laser measuring based on matlab[J].Laser & Infrared,2010,40(1):22 -27.(in Chinese)张婷,张珂殊.基于Matlab的相位式激光测距研究[J].激光与红外,2010,40(1):22 -27.
[2] Jia Fangxiu,Ding Zhenliang,Yuan Feng.Phase-shift laser range finder receiver system[J].Optics and Precision Engineering,2009,17(10):2377 -2384.(in Chinese)贾方秀,丁振良,袁锋.相位法激光测距接收系统[J].光学 精密工程,2009,17(10):2377 -2384.
[3] Wang Zhaohua,Huang Xiangdong.Principle of phase measurement and its application based on All-phase spec-tral analysis[J].Journal of Data Acquisition& Processing,2009,24(6):777 -782.(in Chinese)王兆华,黄翔东.基于全相位谱分析的相位测量原理及其应用[J].数据采集与处理,2009,24(6):777 -782.
[4] Jia Fangxiu,Ding Zhenliang,Yuan Feng,et al.Real-time laser range finding system for moving target based on Allphase fourier transfrorm spectrum analysis[J].Acta Optica Sinica,2010,30(10):2928 -2934.(in Chinese)贾方秀,丁振良,袁峰,等.基于全相位快速傅里叶变换谱分析的激光动态目标实时测距系统[J].光学学报,2010,30(10):2928 -2934.
[5] Lu Yanjie,Xi Zhihong,Wang Jiangbo.Analysis and comparison between FFT and digital correlation theory in phase difference measurement[J].Information Technology,2007,12:105 -108.(in Chinese)路艳洁,席志红,王姜铂.FFT法与数字相关法在相位测量上的比较[J].信息技术,2007,12:105 -108.
[6] Wang Zhaohua,Hou Zhengxin,Su Fei.All-phase FFT spectral analysis[J].Journal of China Institute of Communications,2003,24(11A):6 -19.(in Chinese)王兆华,侯正信,苏飞.全相位 FFT频谱分析[J].通信学报,2003,24(11A):6 -19.
[7] Wang Zhaohua,Huang Xiandong,Yang Wei.The measuring phase method of All-phase FFT[J].World Sci-tech R&D,2007,29(4):28 -32.(in Chinese)王兆华,黄翔东,杨尉.全相位FFT相位测量法(J).世界科技研究与发展,2007,29(4):28 -32.
[8] 高林奎,宋玮.激光测距[M].北京:人民铁道出版社,1977:53-66.
[9] E Oran Brigham.The fast fourier transform and its applications[M].Englewood Cliffs,NJ:Prentice-Hall,1988.
