基于多普勒频谱分析技术的声压复现方法研究
2013-08-17何龙标李良杰王雪晶
何龙标,李良杰,王雪晶
(1.中国计量科学研究院力学与声学所,北京100013;2.北京化工大学信息科技与技术学院,北京100029)
1 引言
空气声声压量值的复现和传递是通过实验室标准传声器进行的,目前主要是通过耦合腔互易法和自由场互易法获得其灵敏度,声压量值帕斯卡(Pa)是寄存在实验室标准传声器的灵敏度上,因此,它是一种间接的量值复现技术。直接的声压量值复现技术包括活塞发声器法、瑞利盘法等。活塞发声器主要依据气体状态方程,适用于低频的声压量值复现,瑞利盘法通过测量瑞利盘在声场中的力矩推算质点速度,计算声压量值,不确定度约0.5 dB。近年来,采用物理原理的方法直接获得声场粒子振速计算声压,实现声压量值的直接复现,是声学计量研究的热点之一。
激光多普勒测速法[1-2]是一种非入侵的测量方式,而且具有高分辨率和线性响应快等特点,这种方法逐渐的应用到流体测量中。1975年,英国学者Taylor K.J[3-4]提出了利用激光法直接测量粒子速度,并用该技术校准传声器。Hann 用激光多普勒的获得声场特性,Davis M R[6]利用此方法获得声场阻抗。在激光多普勒测速的发展过程中,同时也出现了多种信号处理的方法。Shape和 Greated[7-10]等人通过对多普勒信号采用自相关技术估计出流体粒子振速。但是自相关算法中,假设粒子平均流速为零,实际上声场中的粒子往往存在几个mm/s的热运动,这为自相关算法带来较大偏差。本文通过对激光多普勒信号的频谱特征,通过各个频谱分量的比值确定多普勒信号的调制指数,通过对单个频点不同声压级以及同一声压级不同频率下的传声器测量值与通过粒子速度计算的声压值进行对照分析,研究验证该方法的适用性。
2 激光多普勒测速原理
激光多普勒测速原理如图1由激光器产生的光经过分光仪产生两束光以一定的角度(θ)相交形成于椭圆球体,在椭圆球体内形成明暗相间的干涉条纹。条纹的间距为:

式中,λ为光束波长,当粒子通过椭圆区间时,产生的散射光经由光电接收装置转换成电信号,再通过相应的信号处理技术解调出所需的速度信号。

图1 激光多普勒原理图
粒子速度v与调制系数mf有着线性关系[3]:

其中,Ω为调制频率;mf为调制指数。由于多普勒信号是调频信号,根据调频信号[10]在频谱上的特性可知:

其中,Vf(t)为粒子速度值;V0为平均直流速度;J0(mf),J1(mf),J2(mf)为相应的零阶、一阶和二阶贝塞尔函数值;w0为载波频率。由此可知调频波的频谱,有若干个边频分量,每个边频间隔为调制频率。假设调制指数已知,任意两个边频分量的幅值之比即为相对应阶数的贝塞尔函数的比值。相反,在频谱信号确定的条件下,可由各边频的相对幅度来求的调制指数,调制指数获得,便可依据公式(2)计算声场中粒子的振速。
3 实验装置
实验设备主要包括:正弦信号发生器,功率放大器,长3200 mm截面线长为100 mm末端带吸声尖劈的方管,B&K 4180传声器,烟雾发生器和TSI公司激光多普勒测速仪。激光多普勒测速仪探头焦距363 mm,绿光波长488 nm。
由正弦信号发生器产生的正弦信号,经过功率放大器驱动扬声器,在管内形成近似的平面行波声场。烟雾发生器将示踪粒子加入管内,在扬声器的驱动下跟随流体运动。粒子在测量区域内做简谐运动,光电接收装置将散射的光信号转换成电信号,然后将电信号经过混频,滤波,通过信号处理得出速度。将求得的声压与经校准赋值的传声器单元进行测量校准。图2为测量系统的实物图。对于平面波声场,声场中的声压与质点速度有着线性关系,即:p=ρcv,其中,p为声场声压(有效值),ρ为声场介质密度,c为声速,v为质点振动速度有效值。实验条件为23℃,空气的特征阻抗:z=ρc=404 Pa·s/m。

图2 激光多普勒测量粒子振速实物图
4 传声器与测速仪结果比较
在声场中依托激光多普勒技术实现声压的复现,需要经过以下几个过程。首先,声场中的散射光通过光电接收装置变成电信号,实现光电转换。其次,由于接收激光多普勒电信号通常都是经过混频的信号,因而得根据实际情况通过移频将信号的频率移至所需的频带,进行频谱分析。然后通过频谱特征值计算获得声场中的粒子振速,再依据声压与粒子振速之间的关系,获得声压量值。图3为400 Hz,声压级为101.10 dB时的多普勒信号的频谱图,可以求得得到其粒子速度为8.23 mm/s。
实验中由于原始多普勒信号经过40 MHz,因而接收的电信号需要经过近似40 MHz的向下混频。本文频移后的载频为15 kHz,将时域信号作傅里叶变换,取20次平均,以获得良好的信噪比。表1为不同频率点传声器测量值在同一声压级上与测速仪得到结果比较,测量粒子速度介于7.92 mm/s至8.63 mm/s之间,这些频点的偏差不大于0.3 dB。因此,在平面行波声场中,传声器测量的声压与激光测速法复现声压具有较好的一致性。表2是频率为500 Hz在不同声压级测量结果对比,表2中,测量声压级从94~106 dB,最大偏差为0.22 dB,产生偏差的主要因素应该是平面行波管声场的非理想性,即部分反射波和其他噪声,以及传声器测量值本身的不确定度等因素。

图3 声场中多普勒信号的频谱特征
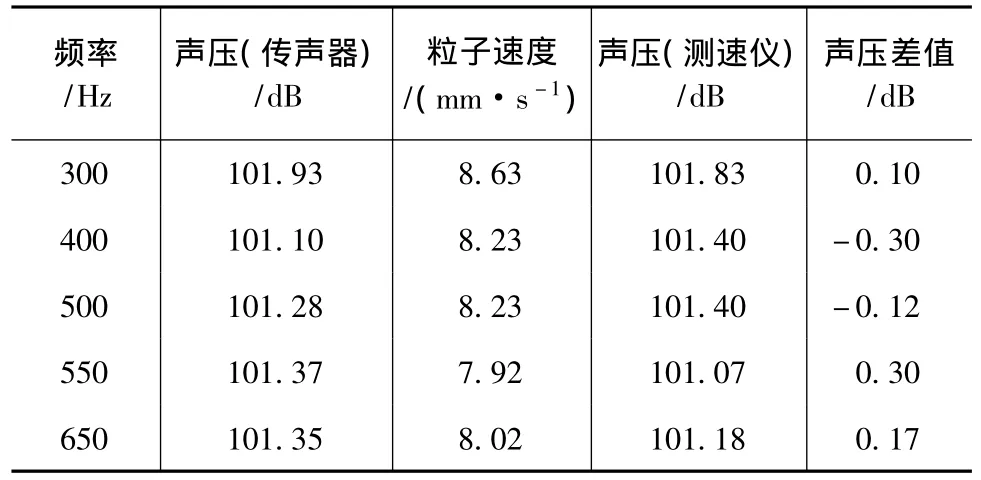
表1 不同频率点两种方法比较

表2 频率500Hz不同声压级的结果对比
5 实验结果分析
传声器测量值和通过激光多普勒仪测量得到的结果有着较好的一致性。但是在某些频点会有较大的偏差。实验中影响实验结果的因素包括以下几项:
5.1 传声器测量值
采用传声器测量声压量值,在250 Hz~1 kHz以内的频段,通常的测量不确定度为0.1 dB。
5.2 示踪粒子
示踪粒子的跟随性是由粒子的粒径决定的,粒径较大的示踪粒子虽然能获得良好的信噪比,但是粒子的跟随性就会下降。烟雾发生器产生的大多数粒子粒径在0.1~10 μm。李恩邦[11]等人对空气中示踪粒子跟随性的数值分析得出,大部分粒径在1 μm的示踪粒子对空气有着较好的跟随性。黄德康[12]等人在激光多普勒测速中散射粒子对信噪比的影响的出,粒子粒径在不大于0.35倍的干涉条纹间距时,能获得良好的信噪比。本文激光干涉仪的条纹间距为3.74 μm,在测量同时要获得良好的跟随性和信噪比,确保大部分示踪粒子的粒径在1 um左右。示踪粒子跟随性引入的测量不确定度需要进一步研究。
5.3 频谱分辨率
在采样时,根据那奎斯特采样定理,采样频率大于信号频率的两倍。本次实验室采样率以采样长度的10倍进行采样,这就导致频谱的最小分辨率为10 Hz,频谱分辨率产生的偏差可能导致各频谱分量取值时产生相应偏差,由此产生的不确定度约为0.01 dB,可以忽略。
5.4 其他因素
其他因素包括空气密度、声场中温度、平面行波管的非理想性等。由于常用的烟作示踪粒子时,在管内作用时间短且在短时间内其平均速度不易下降。继而采用具有挥发性质的葵二酸脂,葵二酸脂在管内作用时间长,在加入管内一段时间易挥发,不易影响空气的密度。但是,示踪粒子的浓度对空气密度的影响是不可忽视的,该部分的不确定度分量正在进一步研究之中。影响实验结果的因素还包括声场中的温度,因为声速是温度的函数;平面行波管的非理想性则关系着粒子振速与声压量值之间的关系。
6 总结
本文通过在平面行波管内的实验结果表明,传声器测量的空气声压与激光测速计算的声压量值具有较好的一致性。激光多普勒信号的频谱分析技术可以用于复现声压量值以及绝对法校准传声器的声压灵敏度。后续研究中将细化各影响因素,对其声压量值的测量不确定度进行准确评估,为光学法直接复现声压量值奠定基础。
[1] Zhang Yanyan,Gong Ke,He Shufang,et al.Progress in iaser doppler velocity measurement techniques[J].Laser& Infrared,2010,40(11):1157 -1162.(in Chinese)张艳艳,巩轲,何淑芳,等.激光多普勒测速技术进展[J].激光与红外,2010,40(11):1157 -1162.
[2] Liu You,Yang Xiaotao,Ma Xiuzhen.Technique of flow field measurement based on laser Doppler velocimetry[J].Laser& Infrared,2012,42(1):18 - 21.(in Chinese)刘友,杨晓涛,马修真.基于激光多普勒测速的流场测试技术[J].激光与红外,2012,42(1):18-21.
[3] Taylor K J.Absolute measurement of acoustic particle velocity[J].J.Acoust.Soc Am,1976,59(3):691 -694.
[4] Taylor K J.Absolute calibration of microphones by a laser Doppler technique[J].J.Acoust.Soc.Am 1981 70(4):939-45.
[5] Hann D B,Greated C A.The measurement of sound fields using laser Doppler anemometry[J].Acustica,1999,85(3):401-411
[6] Davis M R,Hews-Taylor K J.Laser-Doppler measurement of complex acoustic impedance[J].J.Sound Vib 1986,107(3):451-470.
[7] Sharpe J P,Greated C A.The measurement of periodic acoustic fields using photon correlation spectroscopy[J].J.Phys D:Appl Phys 1986:418-423.
[8] Sharpe J P,Greated C A,Campbell DM.The measurement of complex acoustic impedance using photon correlation spectroscopy[J].Acustica 1988,66:282 -292.
[9] Sharpe J P,Greated C A.A stochastic model for photon correlation measurements in Sound fields[J].J.Phys D:Appl Phys,1989,22(10):1429 -1433.
[10] Liang Jun,Sun Zhen.Modulation measurement by spectrum analyzer for the satellite based on the bessel function[J].Journal of Electron Measurement and Instrument,2004,18(z1):84 -87.(in Chinese)梁军,孙震.基于贝塞尔函数的某型号卫星调频信号调制指数测量方法[J].电子测量与仪器学报,2004,18(z1):84-87.
[11] Li Enbang,Li Zhiping,Li Chun,et al.Numerical analysis of following behaviors of particle tracers in turbulent[J].Chinese Journal of Scientific Instrument,2009,30(2):225 -231.(in Chinese)李恩邦,李志平,李淳,等.湍流中示踪粒子跟随性的数值分析 [J].仪器仪表学报,2009,30(2):225-231.
[12] Huang Dekang,Li Cairong,Zhu Maohua,et al.Effect of scattering particle size on signal to noise ratio in Doppler speed measuring with laser device[J].Optical Technology,2003,29(2):164 -165.(in Chinese)黄德康,李彩荣,朱茂华,等.激光多普勒测速中散射粒子的大小对信噪比的影响[J].光学技术,2003,29(2):164-165.
