挠性卫星快速机动光滑控制

饶卫东

1. 北京控制工程研究所,北京 100190 2. 空间智能控制技术重点实验室,北京 100190



挠性卫星快速机动光滑控制

饶卫东1,2

1. 北京控制工程研究所,北京 100190 2. 空间智能控制技术重点实验室,北京 100190

着力求出一种光滑的正弦序列控制，该控制律执行挠性卫星快速机动任务的同时抑制振动。推导得到挠性振动的解析解，当正弦序列加权系数满足一定条件时，中心刚体自动满足静止-静止边界条件，然后通过非线性规划优化加权系数，得到一组残余振动指标次优解。相关公式表明该优化解能较大程度抑制挠性振动，且相应残余振动对模态参数鲁棒性好。数学仿真在5阶模态挠性对象上开展，结果显示该方法有较强的抑振能力，对频率误差不敏感，且控制方法是开环的，适合作为卫星快速机动前馈输入。 关键词 挠性卫星； 快速机动； 前馈输入； 非线性规划

航天任务中质量更轻意味着成本更低廉，能量消耗更少。航天器的轻型化和大型化使得大挠性问题日益突出，这使得航天器在姿态机动时，更容易产生挠性振动。而太空环境的微重力和微阻尼，又使得振动很难衰减。很多航天任务中姿态控制都遇到了困难，比如机械臂抓取、移动重物，敏捷卫星姿态快速机动等。如何在这些任务中既快速又稳定地控制挠性对象是一个重大挑战。

研究人员经过几十年积累，充分解答了挠性卫星的时间最优控制。Singh等[1]给出了纯粹时间最优控制的数值解法，得到了包含4阶挠性模态对象的Bang-Bang控制最优解，结果显示挠性卫星实现静止到静止的快速机动，需要的时间与纯刚体卫星的相差不多。张洪华等[2]在脉冲序列控制的基础上，提出了基于非约束模态方程的方波序列控制方法，并给出了使得机动时间最小的方波规划方法，其优点是控制输出是方波而非脉冲，因而特别适合卫星上的喷气推力器控制模式，也适合飞轮控制模式。

Bang-Bang控制给出快速机动时间的下界，其他方法的机动时间都要更长，更多的研究人员着手研究光滑的次优控制。一部分学者直接研究Bang-Bang控制的光滑逼近，增大一点机动时间得到连续平滑的控制函数，使得激发的过程挠性振动大幅度减少。Albassam等[3]研究了一类挠性卫星的近似时间最优控制，考虑柔化Bang-Bang控制曲线，即考虑输入受限并且一阶导数受限的刚体卫星时间最优控制，仿真表明该柔化曲线比Bang-Bang控制激发的挠性振动小。另一部分学者从能量最优角度研究光滑控制，Hindle[4]等研究了挠性卫星加权最小能量冲击控制，得到了最优控制解析解，作者研究了模型参数不确定性对于残余振动的影响，通过引入新状态变量描述不确定性，得到了对挠性频率有鲁棒性的控制解析解。

其他研究人员还考虑了非最优控制方法，如变结构方法。王晓磊等[5]研究挠性卫星在控制受限情况下，采用抛物线型滑动模态设计一种过渡过程性能很好的变结构控制器，并且分析了这种非线性滑动模态的稳定性。周连文等[6]采用等速趋近率的滑模变结构控制策略进行大角度机动控制，并通过最优控制理论设计弹性稳态器，抑制由于刚体运动而激发的弹性振动，实现旋转机动的同时，有效抑制弹性振动。这些方法在干扰和不确定性影响下的表现比最优控制好，但只关心了整个系统闭环稳定性，对快速机动过程中挠性振动的抑制和规避分析很少。

Chen[7]等研究前馈和反馈相结合的控制方法，其中前馈输入是光滑的正弦函数形状，仿真表明平滑前馈控制有助于抑制挠性振动，而反馈控制有助于应对外界干扰。正弦函数平滑且意义明确易于设计，常用于挠性结构参考轨迹设计。文献[8]和[9]利用单正弦或者正弦序列设计挠性对象快速机动任务控制器，前者能方便地分析执行机构的机动能力，后者则对挠性振动进行优化。

本文采用正弦序列控制方法，考虑了对象控制受限和挠性振动受限，并优化了快速机动后的残余振动。该方法满足一定意义上的振动指标最小，设计简单，且受挠性参数影响小。作为对比，同时研究了其它两种开环控制方法，包括光滑刚体控制[3]和Bang-Bang控制。数学仿真表明：作为开环控制，本文方法在快速机动任务中，产生的过程振动和残余振动减少，适合工程应用。

1 研究对象和问题描述

研究的对象为中心刚体带挠性附件类，如图1所示，对象仅能绕中心轴转动。中心刚体中的动量轮和角度敏感器为执行机构和测量部件，挠性板通过刚挠连接体固定于中心刚体。假设在快速机动时，挠性附件为欧拉-伯努利悬臂梁，在任何时候形变很小可近似线性化。

图1 试验平台示意图

采用混合坐标法建立挠性卫星模型，给出动力学方程

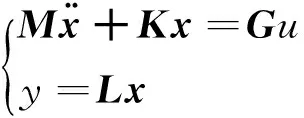
(1)

式中x为n+1维模态向量；u为控制输入；y为角度输出；M为惯量阵；K为刚度阵；G为输入系数阵。

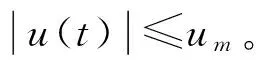
(2)

式中，z为非约束刚性模态；q=(q1,q2,…,qn)T为非约束挠性模态；φ0为刚体增益；φ1=(φ1,φ2,…,φn)T为模态增益阵。

进一步，上述模型写成状态空间形式

(3)

非约束模态；A,B,C为系统阵、输入输出阵。

2 正弦序列优化控制

2.1 正弦序列介绍

利用已知的一类平滑控制函数，经过加权组合优化得到控制解满足“较小程度”激发挠性振动。这类平滑控制函数如果本身性质良好，那么得到的优化控制解对挠性参数也不敏感。正弦函数就是这样一类函数，其任意阶导数有界，平滑特性非常好。

定义θf为机动角度，tf为机动时间，φ0为刚体增益。给定正弦系列控制输入u(t)

(4)

其中参数满足

那么基于方程(2)的刚体姿态响应x0(t)为

(5)

其中，

(6)

很显然，控制输入式(4)的参数条件使得刚体姿态x0(t)满足边界条件

也就是说，在控制律式(4)的作用下，卫星的刚体部分将实现静止到静止的姿态定向任务。为了得到激发挠性振动较小的控制，需要对参数c1,c2,…,cm进行优化。一般而言，只要m不是特别大，输入控制式(4)都很平滑。特殊的当c1=1,c2=…=cm=0时，曲线为单正弦控制输入，常在工程中使用。

2.2 残余振动的优化

下面讨论正弦序列作用下的残余振动。正弦序列由一组正弦函数构成，系数之和等于1保证刚体姿态到达目标。加权系数仍然还有自由度，利用这一点对残余振动能量优化。对于第i阶挠性模态，在控制律(4)作用下，系统(3)在tf时刻残余振动的表达式为

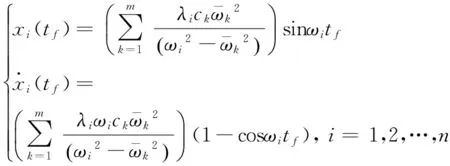
式中，λi只与第i阶模态有关，与正弦序列无关。

残余振动确定项，与机动时间无关。

2)ei=ωitf

残余振动随机项，与机动时间有关。

为降低残余振动随机项ei大小，只有调节机动时间tf。若此时卫星挠性耦合很强，需要同时优化多个模态残余振动时，tf显然不足以优化所有模态。另外，残余振动随机项ei对挠性频率ωi相当敏感，此时优化ei的实用性不大。图2可以验证上述分析：对于快速机动tf=15s的挠性对象，若挠性频率ωi为3rad/s左右，则随机项ei误差±20%置信频率区间为2.99～3.08rad/s，即ωi容许频率误差仅为±1.5%左右。

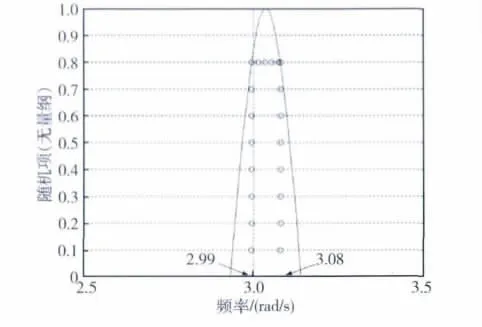
图2 随机项敏感曲线

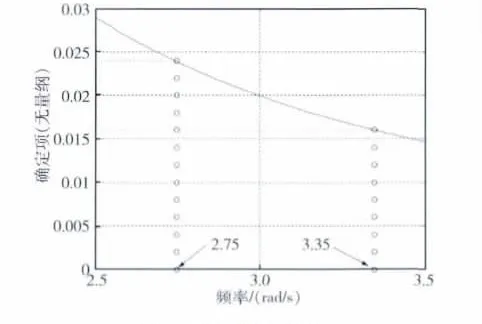
图3 确定项敏感曲线

为了优化残余振动确定项fi，计算频率ωi偏离时fi的变化

(8)

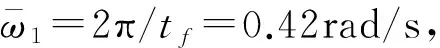
2.3 控制算法求解

由于控制输入被限制为正弦序列，得到的将是次优解，构造残余振动指标，并对其中的确定项优化，得到下面的确定时间次优控制

次优指标：

(9)

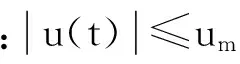
边界条件：自动满足

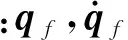
由式(2)及控制律(4)可求挠性模态

(10)

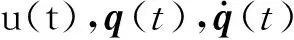
非线性规划

minJ(C)

s.tU(C)≤um,Q(C)≤qmn

c1+c2+…+cm=1

(11)

其中:

3 数学仿真

3.1 正弦序列优化控制

为了验证方法的有效性，本节利用相关动力学模型[10]进行数学仿真。表1给出了该装置的详细参数，总惯量为I=20kg·m2，最大饱和力矩um=1N·m。保留了前5阶挠性模态信息用于数学仿真，本文的控制方法优化前2阶主要模态。

表1 对象标称参数

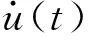
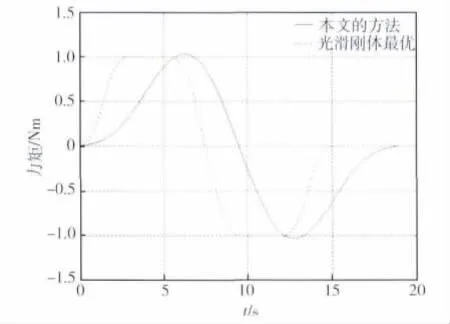
图4 控制输入曲线(15s机动90°)

仿真90°的快速机动，本文方法的机动时间是19s，而光滑刚体控制的机动时间是15s。2种方法最大控制力矩相同时，本文方法的机动时间稍长。本文2.3节中的参数取值为：Q1=Q2=I(单位阵)，正弦序列包括2个频率分量，即m=2。图5给出本组仿真的控制力矩曲线，2种控制方法始终都光滑连续，在初始时刻、末端时刻和开关时刻，两种方法的曲线一阶导数和二阶导数都连续有界。尤其是本文的方法在整个机动过程都没有切换存在，任意阶导数有界，一致性非常好。

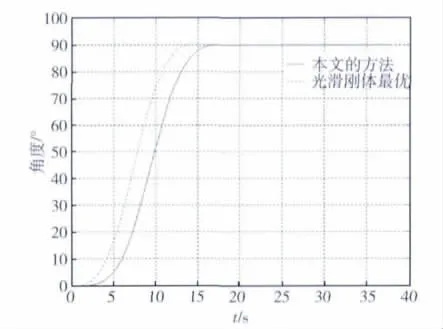
图5 姿态输出曲线(15s机动90°)

图6和7给出了前两阶模态的振动情况。本文采用的控制方法整体性能很好，整个机动过程各阶挠性模态振动都得到抑制。尤其是在最大挠性振幅处，本文采用的方法要明显优于光滑刚体控制。唯一不足的是，延长了机动时间，牺牲了执行机构快速机动能力。

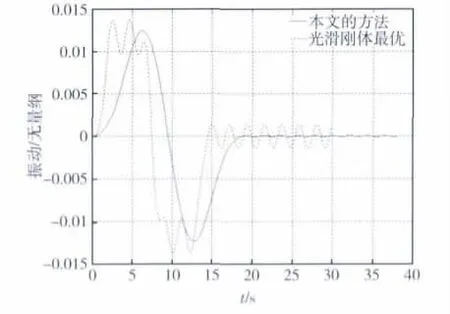
图6 一阶模态(15s机动90°)

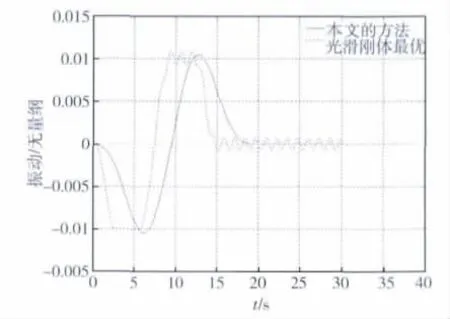
图7 二阶模态(15s机动90°)

接下来的仿真是针对非标称系统的。由于光滑刚体控制律的设计和挠性参数无关，所以该方法对挠性参数的鲁棒性较好。2.2节分析了本文采用的控制方法受参数不确定性的影响，因此可以预见本文的控制方法对挠性参数的鲁棒性也较好。

同3.1节的仿真(15s机动90°)，此时挠性对象频率偏离标称值20%，前两阶挠性频率为ω1=2.3rad/s,ω2=3.9rad/s。图8为本文控制方法的姿态曲线，从图中可以看出，本文方法的鲁棒性非常好，在挠性频率偏差情况下，抑制残余振动的能力受影响很小。

图8 本文方法控制的姿态角(频率偏差20%)

3.2 单频率正弦控制

工程中为了设计简单，有时采用单频率控制(m=1)，这样就失去了对残余振动的优化。本节的仿真我们将能看到，这种简单控制方法抑制挠性振动不尽如人意，但是和一般的非光滑控制相比，激发的挠性振动还是要小很多。

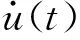
图9 控制力矩(15s机动90°)

图10 一阶模态(15s机动90°)

但作为光滑的控制方法，单频率正弦控制激发的挠性振动要远小于非光滑控制，为此本节还额外进行了多组仿真，这其中包括了Bang-Bang控制方法的仿真。并且引入过程振动能量这个概念，定义过程振动能量E：

表2给出了各种方法用于姿态快速机动90°时的过程振动能量E。单频率正弦控制(一)和光滑刚体控制(二)的指标E很接近，这说明方法(一)和(二)激发挠性振动较小，是温和、光滑的控制方法。最后还给出Bang-Bang控制(三)的过程能量E，要远大于其他两种控制方法。

4 结论

正弦序列优化控制设计简单，由几个倍频的正弦信号组成，整个机动过程中一致性好，激发的过程振动并不大。更重要的是，该方法能够通过控制加权系数，减少残余振动能量并且对模态信息不敏感，所以不失为一种较好的开环输入控制。正弦序列优化控制的缺点主要有2点：1)正弦序列个数受到对象挠性频率的限制，在进行残余振动优化时，只能考虑少数几个挠性模态，如果快速机动时间很短，正弦序列个数大大受限，优化方法几乎就不能使用；2)为了限制残余振动，该方法需要更大的输入力矩，会牺牲一定程度的快速机动能力。

表2 机动90°过程振动能量

把该方法和反馈控制相结合，为应对快速机动时外界的干扰力矩将是下一步的工作重点。

[1] Singh G, Kabamba P T, McClamroch N H. Planar Time-Optimal Rest-to-Rest Slewing Maneuvers of Flexible Spacecraft[J]. Journal of Guidance, Control and Dynamics, 1989, 12(1):71-81.

[2] 张洪华，黎康，赵宇.挠性卫星姿态快速机动控制[J].中国空间科学技术，2005，25(1):53～59. (Zhang Honghua， Li Kang， Zhao Yu . Fast Maneuver Control of Flexible Satellite System[J].Chinese Space Science And Technology , 2005，25(1):53～59.)

[3] Albassam B A. Optimal Near-Minimum-Time Control Design for Flexible Structures[J]. Journal of Guidance, Control and Dynamics, 2002, 25(4): 618-625.

[4] Hindle T A, Singh T. Robust Minimum Power/Jerk Control of Maneuvering Structures[J]. Journal of Guidance, Control and Dynamics, 2001, 24(4):816-826.

[5] 王晓磊，吴宏鑫，李智斌.挠性航天器非线性滑动模态控制和试验研究[J].宇航学报，2001，22(6):50-56. (Wang Xiaolei,Wu Hongxin,Li Zhibin. The Nonlinear Sliding Mode Control and Experiment Research for Flexible Spacecraft[J]. Journal of Astronautics，2001，22(6):50-56.)

[6] 周连文，周军.挠性航天器大角度机动的变结构控制[J]. 航天控制，2003,21(3):48-52.(ZHOU Lian wen, ZHOU Jun. Variable Structure Control for Large Angle Maneuvering of Flexible Spacecraft[J].Aerospace Control, 2003, 21(3): 48-52.)

[7] Chen H J, Agrawal B N. Method of Slewing the Spacecraft to Minimize Settling Time[C]. AIAA Guidance, Navigation, and Control Conference and Exhibit. Monterey, California, 5-8 August, 2002.

[8] 宗红，雷拥军.基于控制力矩陀螺的卫星姿态快速机动控制方法研究[J]．空间控制技术与应用，2007,33(5):11-16.(Zong Hong, Lei Yongjun. Research on Control of Satellite Attitude Rapidly Maneuvering with Control Moment Gyros[J].Aerospace Control and Application,2007,33(5):11-16.)

[9] Zhao H C, Chen D. Optimal Motion Planning for Flexible Space Robots[C]. International Conference on Robotics and Automation, Minneapolis, Minnesota, April 1996.

[10] 饶卫东，徐李佳．单轴挠性卫星快速机动试验平台[J]．空间控制技术与应用，2011，37(5):59-62.(Rao Weidong,Xu Lijia.A Simulation TestBed for Rapid Maneuver Experiment of Flexible Satellite[J].Aerospace Control and Application, 2011，37(5):59-62.)

Smooth Control for Quick Maneuver of Elastic Satellites

RAO Weidong1,2

1. Beijing Institute of Control Engineering, Beijing 100190, China 2. Science and Technology on Space Intelligent Control Laboratory, Beijing 100190, China

Thisarticleconcentratesonakindofsmoothcontrolwhichconsistsofseriesofsinusoids.Themethodcarriesoutquickslewingforelasticsatellitesandmeanwhilerestrainsvibrationsuppression.Analyticsolutionsofelasticvibrationareobtainedbyderivation.Rigidbodywillberesttorestautomaticwhencoefficientsofsinusoidssatisfysomeequations,andthenoptimizationisdonetowardsthecoefficientswhichleadtoaresidualvibrationsuboptimalsolutionbynonlinearprogramming.Relevantformulashowstheoptimizedsolutionsuppressesmuchvibrationandpossessesgreatrobustnesstowardselasticparameters.Numericsimulationiscarriedoutonaplantwithfiveelasticmodes.Theresultsindicatethemethod’sstrongabilityinrestrainingresidualvibration.Themethodhereisanopen-looponewhichcanbeusedasfeedforwardcontrol.

Elasticsatellites;Quickmaneuver;Feedforwardcontrol;Nonlinearprogramming

2012-06-13

饶卫东(1985-)，男，江西人，博士研究生，主要研究方向为挠性卫星控制。

V448.22

A

1006-3242(2013)05-0069-07