基于新型趋近率的挠性航天器滑模变结构控制

于亚男 孙 博 孟秀云

1.北京理工大学宇航学院，北京100081 2.北京特种机电研究所，北京100012



基于新型趋近率的挠性航天器滑模变结构控制

于亚男1孙 博2孟秀云1

1.北京理工大学宇航学院，北京100081 2.北京特种机电研究所，北京100012

针对应用切换函数带来的挠性航天器滑模变结构控制力矩的高频抖振问题，提出了一种趋近率的改进方法。首先应用连续的饱和函数替换指数趋近率中的符号函数，其次针对饱和函数带来了边界层厚度是固定值，无法到达滑模面的问题，应用模糊逻辑对改进后的指数趋近率进行自适应智能处理。将此控制算法应用于挠性航天器的姿态机动控制中，数学仿真结果表明此控制算法可以有效地抑制控制力矩的高频抖振，并获得良好的控制效果。 关键词 滑模变结构；高频抖振；饱和函数；模糊逻辑

滑模变结构控制器在进入滑动模态后，具有对系统参数的变化和外部干扰不敏感的特点，表现了良好的鲁棒性和抗干扰性，因此广泛应用于挠性航天器的姿态控制问题[1-5]。但是滑模变结构控制器由于切换函数的存在带来了控制力矩的高频抖振，可能会引起挠性附件谐振，导致挠性振动不能快速收敛，甚至对航天结构产生破坏性影响。为了解决这个问题，研究者提出用具有连续性的饱和函数代替符号函数，饱和函数的边界层厚度是一个常数，边界层厚度过大，系统的解虽然存在且唯一，但系统轨迹不可能渐近收敛到所给定的切换平面s=0之上，而此常数过小则接近于符号函数，不能有效的抑制高频抖振[6-7]，因此要寻求一种实时的改变边界层厚度的方法。

模糊控制作为一种智能控制方法，是一种以模糊集合论、模糊语言变量和模糊逻辑推理为基础的一类计算机控制策略，是一种非线性控制。模糊控制不是采用纯数学建模的方法，而是结合专家的知识和思维，进行学习与推理、联想和决策的过程，由计算机来识别和建模，并进行控制。模糊控制系统的鲁棒性强，干扰和参数变化对控制效果的影响被大大减弱，尤其适合于非线性、时变及纯滞后系统的控制。

本文提出利用模糊控制实时改变饱和函数作用程度的方法。基于挠性航天器姿态动力学模型，首先应用连续的饱和函数代替滑模变结构控制器中的切换函数，控制器的高频抖动得到了有效地抑制，其次用模糊逻辑算法对趋近律参数进行了自适应智能处理，利用模糊控制器来优化改进的滑模变结构的趋近率参数，以切换面s以及其导数的值作为模糊控制器的输入量，改进的指数趋近率的2个系数作为输出量，对改进的变结构控制算法进行了实时优化。经过仿真发现，此算法能有效抑制控制器的高频抖振，并且在实现挠性航天器姿态机动的同时使挠性附件低阶振动模态的收敛速度加快。

1 挠性航天器姿态动力学建模

挠性航天器一般由刚性主体和挠性附件构成，其运动学由主体的姿态运动决定，利用四元数方法描述挠性航天器的姿态运动学方程[8]为：

(1)

其中，[q0,qT]T为描述航天器姿态的单位四元数向量，ω为航天器刚性主体相对于惯性空间的角速度矢量

用喷管或者反应轮驱动的带有挠性附件航天器姿态动力学方程为：

(2)

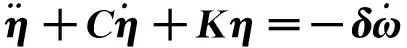
(3)

2 基于新型趋近率的滑模变结构控制

器设计

滑模变结构控制系统是一种特殊的非线性系统，其非线性表现为控制的不连续性，是对控制函数的一种开关切换动作，根据系统实时的状态(偏差以及各阶导数等)，以跃变的方式有目的的变化，迫使系统沿预定的“滑动模态”状态运动，滑模变结构控制系统具有快速响应、对控制对象的参数变化及扰动不敏感的优点。对于挠性航天器动力学系统，由式(3)得：

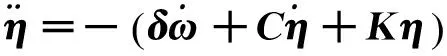
(4)

将式(4)带入式(2)得：

由上式可以推出：

(5)

其中，Jmb=J-δTδ，滑模变结构控制器的切换函数为：

s=ω+k1q

(6)

由上式求导得：

(7)

(8)

将式(5)和(8)带入式(7)中：

则指数趋近率：

控制率u为：

此控制率应用到实际系统，要涉及到状态量的测量问题，由于挠性附件的相关变量在实际中是难以测得的，所以在控制率中省略挠性模态的相关量，得到的控制率为：

其中：K1=Jmbε,D1=Jmbr，这里K1和D1为正定矩阵。

选取的滑模面s=ω+k1q在滑模面s=0上具有渐进稳定性的证明：

其中W为对角正定矩阵，则Ve为正定函数，当且仅当q=0时，Ve=0。

Lyapunov函数对时间求导得

2.1 用饱和函数改进滑模变结构趋近率

在实际滑模变结构系统中，由于参数的不确定性以及外界干扰等因素的影响，系统的状态到达滑模面后，有可能不是保持在滑模面上作滑动运动，而是在滑模面附近作来回的穿越运动，甚至会产生极限环振荡，这种现象称为抖振。它有可能激励起系统中未建模高频成分，引起系统的高频振荡，对系统造成危害。因此削弱或消除抖振是变结构控制在实际应用中要着重解决的重要问题，一些学者在这方面开展了广泛而深入的研究。趋近律方法是一个比较有效的方法。一个好的趋近律不仅可以削弱系统的抖振，还可以加快系统从任意初始状态到达滑模面的时间，提高系统的鲁棒性。指数趋近率虽然有一定的优越性，但是由于包含符号函数，开关的切换动作造成控制的不连续性是高频抖振发生的根本原因。

为了解决滑模变结构控制器带来的固有抖振问题，采用连续的饱和函数代替符号函数。饱和函数的表达式为：

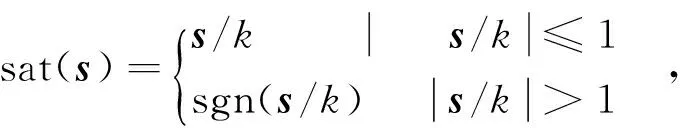
k为边界层的厚度，可以通过调节边界层的厚度来控制滑动模态的到达时间。

根据上述理论，用饱和函数改进的滑模变结构控制率的表达式为：

(9)

2.2 用模糊逻辑算法实现变系数滑模变结构趋近率

模糊控制算法具有适应被控对象非线性和时变性的特点，并且传统的控制方法对系统进行控制时，需要有控制系统精确的数学模型，模糊控制不需要精确地函数指向关系，它把人类的自然语言表达的控制策略通过模糊集合和模糊推理转化成数字或数学函数，再用计算机来实现控制。滑模变结构控制率设计控制器的关键在于如何加快系统到达滑动模态的速度，以及削弱控制信号的高频抖振。

由于用饱和函数设计的趋近率，根据饱和函数中边界层的厚度为固定值k，因此无论k取的值有多小，系统都无法完全到达滑模面，在使用滑模变结构控制时根据切换函数的值，希望能对改进的指数趋近率的2个系数进行实时修正，使系统到达滑模面，但无法推导出切换函数的值与改进的指数趋近率2个系数的确切函数关系，因此采用模糊控制算法，可以根据实时计算的切换函数的值通过模糊推理智能算法，对指数趋近率系数进行修正。

由上一节获得的改进的滑模变结构控制率为：

图1 模糊控制实现原理图

对改进的滑模变结构控制率参数K1，D1进行实时模糊的原理图介绍如下：

1)量化因子Ks，Kds

2)模糊化模块

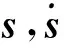
模糊子集为负(N)，隶属函数表达式为

模糊子集为零(Z)，隶属函数表达式为

模糊子集为正(P)，隶属函数表达式为

3)模糊推理模块

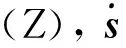
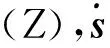
4)清晰化模块

模糊推理输出的K1和D1对应的模糊集合是由多条模糊控制规则所得结论的综合，其隶属函数多是分段、不规则的形状，清晰化的目的就是将它们等效成对应的清晰值，在模糊论域中找到一个清晰值来代表它，常用的有面积平分法、重心法和最大隶属度法。本文应用的重心法清晰化就是求出模糊集合隶属函数曲线和横坐标包围区域面积的中心，选这个中心对应的横坐标值作为这个模糊集合的代表值，设论域U上F集合A的隶属函数为A(u)，u∈U，则面积中心uce对应的横坐标按照定义为

此值即为与输出变量K1和D1对应的F集合中的清晰值。

5)比例因子Kk，Kd

清晰化处理后的K1和D1的对应值是包含在模糊论域U中的清晰值，此模糊论域和后面执行机构所需的物理论域N未必一致，同量化因子的原理一样，比例因子的作用在于将清晰化后的输出值转化为能够和外界匹配的数值。

3 仿真分析

为了验证方法的有效性，采用文献[8]给出的物理参数，只研究挠性振动的低阶模态，带有挠性附件航天器姿态动力学方程(2)和(3)中的结构参数为：

刚性主体的惯性矩

挠性附件与刚体动力学的耦合矩阵

仿真时取挠性模态的前4阶，所以挠性模态的振动频率为：ωn1=0.7681rad/s，ωn2=1.1038rad/s，ωn3=1.8733rad/s，ωn4=2.5496rad/s；挠性模态振动阻尼比为：ζ1=0.0056，ζ2=0.0086，ζ3=0.013，ζ4=0.025。

为了研究方便，这里设外部空间干扰力矩D为0。

四元数描述的姿态初始值为：

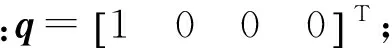
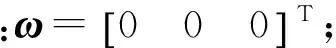
将滑模变结构控制算法，应用连续函数改进的滑模变结构控制算法和使用模糊算法的控制器分别进行仿真。

1)滑模变结构控制

图2为用滑模变结构控制算法对挠性航天器的姿态控制。滑模变结构控制器的仿真参数为：K1=100I3，D1=0.8I3，I3表示3×3阶单位矩阵。

由图2可以看出，姿态角和姿态角速度都在70s左右稳定，挠性振动的一阶模态有收敛趋势，但在200s时收敛效果仍不明显，控制力矩有高频抖振。

2)用饱和函数改进的滑模变结构控制

图3为用饱和函数改进的滑模变结构控制算法对挠性航天器的姿态控制，饱和函数的边界层的厚度k=0.0001。

由图3可以看出，姿态角和姿态角速度都在70s左右稳定，挠性振动的一阶模态有收敛趋势，但在200s时收敛效果仍不明显，控制力矩的高频抖振得到有效抑制，但是姿态角速度在稳定后仍在以微小幅度振荡。

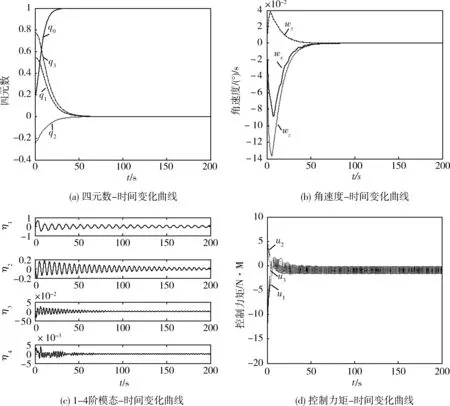
图2 滑模变结构控制算法

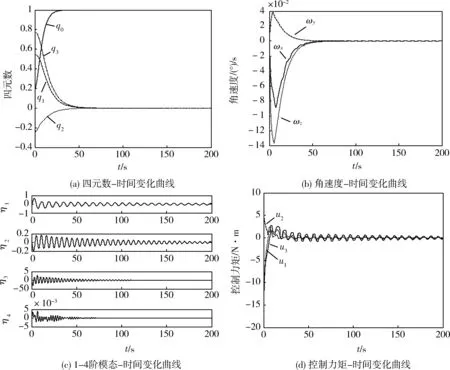
图3 饱和函数改进的滑模变结构控制算法

3)模糊滑模变结构控制

图4为应用模糊控制算法对2.1节中饱和函数改进的滑模变结构控制率中的指数趋近率参数进行实时优化的结果，选取量化因子为Ks=1，Kds=2，比例因子为Kd=100，Kk=10。

图4 模糊滑模变结构控制

应用重心法清晰化，实现挠性航天器的模糊滑模变结构控制得到的仿真结果如图4，可以看出此方法实现的姿态和角速度在70s左右稳定，挠性振动的一阶模态在100s收敛至0，控制力矩的高频抖振得到抑制，控制力矩的值收敛效果很好。

4 结论

在滑模变结构控制的基础上，应用连续的饱和函数代替符号函数，有效地解决了控制力矩的高频抖振问题，但是用这种方法改进后的变结构控制器由于饱和函数的边界层有一定的厚度，出现了姿态角速度不能完全收敛为0的情况，挠性附件振动收敛效果改进也不明显。因此把模糊逻辑算法与改进的滑模变结构控制相结合，对改进的指数趋近率的系数进行实时解算，经过仿真分析，模糊控制算法优化了改进的滑模变结构控制，边界层厚度问题得到了有效地解决，控制力矩的高频抖振得到了有效地抑制，挠性附件的低阶振动模态收敛速度也明显加快。该算法继承了滑模变结构控制的鲁棒性和抗干扰性，设计的控制器更具实用价值。

[1] Yallaprgda S V, Heck B S，Finney J D. Reaching Conditions for Variable Structure Control without Output Feedback [J]. Journal of Guidance, Control and Dynamic, 1996, 19(4):848-853.

[2] 管萍，刘小河，刘向杰.挠性卫星的变结构姿态控制[J].控制理论与应用,2007,24(3):480-484.(GUAN Ping, LIU Xiaohe, LIU Xiangjie. Variable Structure Attitude Control of Flexible Satellite [J]. Control Theory & Applications, 2007,24(3):480-484.)

[3] 胡庆雷，马广富.基于变结构/输入成形的航天器振动抑制方法[J].哈尔滨工业大学学报,2006,38(10):1769-1777. (HU Qinglei, MA Guangfu. Flexible Spacecraft Attitude Maneuvering and Vibration Damping Using Variable Structure Control Input Shaping [J]. Journal of Harbin Institute of Technology, 2006,38(10):1769-1777.)[4] 周连文，周军，李卫华.基于遗传算法的挠性航天器大角度机动的变结构控制[J].上海航天,2005,22(1):15-18.(ZHOU Lianwen, ZHOU Jun, LI Weihua. Variable Structure Control for Large Angle Maneuvering of Flexible Spacecraft Based on Genetic Algorithm [J]. Aerospace Shanghai, 2005, 22(1):15-18.)

[5] 黄显林，卢鸿谦，张永安，等.挠性结构的模态变结构控制[J].哈尔滨工业大学学报,2001,33(1):52-59.(HUANG Xianlin, LU Hongqian, ZHANG Yongan, HU Hengzhang. Independent Moda-Space Variable Structure Control for Flexible Structure [J]. Journal of Harbin Institute of Technology, 2001,33(1):52-59.)

[6] But Ron J A, Zinober A S I. Continuous Approximation of Variable Structure Control[J]. International Journal of Systems Science. 1986,17(6):875- 885.

[7] Shyu K K, Shieh H J. A New Switching Surface Sliding-mode Speed Control for Induction Motor Drive Systems[J]. IEEE Transactions on Power Electronics,1996,11(4):660- 667.

[8] Stefano D G. Output Stabilization of Flexible with Active Vibration Suppression [J]. IEEE Transactions on Aerospace and Electronic Systems,2003,39(3):747-759.

[9] 梅红，王勇.快速收敛的机器人滑模变结构控制[J].信息与控制，2009,38(5):552-557.(MEI Hong, WANG Yong.Fast Convergent Sliding Mode Variable Structure Control of Robot [J]. Information and Control, 2009,38(5):552-557.)

[10] 高为炳.变结构控制器理论及其设计方法[M].北京：科学出版社，1996，54-63.

[11] 金鸿章，罗延明，肖真,等.抑制滑模抖振的新型饱和函数法研究[J].哈尔滨工程大学学报，2007，28(3):288-291.(JIN Hongzhang, LUO Yanming, XIAO Zhen, ZHANG Xiaofei. Investigation of a Novel Method of Saturation Function for Chattering Reduction of Sliding Mode Control [J]. Journal of Harbin Engineering University, 2007, 28(3):288-291.)

The Sliding Mode Variable Control of Flexible Spacecraft Based on a Novel Reaching Law

YU Yanan1SUN Bo2MENG Xiuyun1

1.Beijing Institute of Technology, School of Aerospace Engineering, Beijing 100081, China 2.Beijing Special Electromechanical Research Institute, Beijing 100012, China

Theproblemofhighfrequencychatteringofcontroltorqueisfocusedwhentheslidingmodevariablestructure(SMVS)ofintroducingsignfunctionisused.Firstly,ameansofusingcontinuousfunctioninsteadofsignfunctionisproposedtoimprovetheexponentialapproachlaw.Secondly,aimingattheproblemthatthethicknessofboundarylayerisfixedvalueandcannotreachtheslidesurfacewhenthecontinuousfunctionisused,theexponentialapproachlawisoptimizedintimebyfuzzylogic.Thiscontrolalgorithmisappliedtothecontrolofflexiblespacecraftmaneuvering.Thesimulationresultsshowthatthehighfrequencychatteringofcontroltorqueisrestrainedeffectivelyandthecontrollerhasgoodperformance.

SMVS;Frequencychattering;Continuousfunction;Fuzzylogic

2012-09-12

于亚男(1984-)，女，内蒙古人，博士研究生，主要研究方向为挠性航天器大角度姿态机动控制；孙博(1975-)，女，辽宁人，工程师，主要研究方向为兵器科学与技术；孟秀云(1964-)，女，内蒙古人，教授，博士研究生导师，主要研究方向为飞行器制导、控制系统设计及系统仿真。

V448.2

A

3242-1006(2013)05-0062-07