基于遗传模糊推理的自适应UKF组合测姿滤波算法

肖文健 路 平

军械工程学院无人机工程系, 石家庄 050003



基于遗传模糊推理的自适应UKF组合测姿滤波算法

肖文健 路 平

军械工程学院无人机工程系, 石家庄 050003

针对常规UKF在组合测姿中自适应性不足的问题，提出一种基于遗传模糊推理的自适应UKF组合测姿滤波算法。首先建立了基于模糊推理的自适应UKF，利用模糊推理系统对组合测姿系统的量测噪声统计特性进行调整，以实现状态的准确估计。然后利用遗传算法对模糊推理系统的隶属度函数参数进行了离线优化，以提高系统精度。最后以陀螺仪、加速度计和磁强计组成的组合测姿系统进行了实验。实验结果表明，基于遗传模糊推理的自适应UKF在量测噪声变化时仍能保持较好的测量精度，具有较强的自适应能力。 关键词 组合测姿； 无迹卡尔曼滤波； 遗传算法； 模糊推理； 自适应

姿态信息是飞行器飞行过程中所需要的最基本的导航参数，是导航过程的基础。捷联姿态系统就是把惯性单元等传感器所测得的信息经导航计算机处理成姿态参数的系统。目前扩展卡尔曼滤波(EKF)和无迹卡尔曼滤波(UKF)是飞行器姿态估计的常用方法。而在一般情况下，飞行器姿态确定问题属于严重的非线性问题，EKF容易引入线性化误差，从而降低滤波精度。UKF基于UT变换来逼近非线性系统状态后验分布，不需要线性化，因此精度高于EKF。此外，相对于EKF，UKF在滤波过程中无需计算雅可比矩阵，比EKF更容易实现。然而，不论是EKF还是UKF都属于经典卡尔曼滤波的扩充，和卡尔曼滤波一样，它们都是以准确的数学模型和噪声统计特性已知为基础的[1-3]。在飞行器姿态测量中，系统和观测模型多为已知，但由于系统本身元器件的不稳定，系统过程噪声和观测噪声的统计特性难以准确描述，而且当飞行器周围环境变换或者运动状态剧烈变换时，系统的过程噪声统计特性和观测噪声统计特性将会发生很大的变化，此时传统的EKF或UKF滤波的精度和稳定性都会大大降低。针对系统的过程噪声统计特性和观测噪声统计特性的时变性，近几年国内外相关领域的学者进行了深入的研究，提出了一些致力于估计噪声统计特性的方法，主要有相关法自适应滤波[4]、Sage-Husa自适应滤波[5]、强跟踪滤波[6]、渐消因子算法[7]、神经网络辅助法[8]和模糊推理[9]等。Mehra将这些估计方法划分为4类：贝叶斯估计、极大似然估计、相关估计和协方差匹配估计。由于受到计算量和未知变量的限制，贝叶斯估计、极大似然估计和相关估计并没有得到普及。协方差匹配方法是一种传统的基于滤波新息来估计协方差的自适应方法，它将残差的实际值等效为残差的理论值。该方法性能受滑动窗口大小的影响，匹配结果波动性较大。由于模糊逻辑具有处理不确定性问题的能力，将其与传统卡尔曼滤波结合，可以增强卡尔曼滤波的自适应调节能力，进而提高其抗干扰性能。在已有的模糊自适应卡尔曼滤波中，模糊推理系统大都依靠经验或先验知识设计，虽然可以通过定性分析得到比较准确的模糊规则，但是很难通过定量分析得到精确的隶属度函数，因此不能保证系统输出精度为最佳。遗传算法是智能优化方法中应用最为广泛也最为成功的算法[10]，是一种基于自然选择和遗传变异等生物进化机制的自适应全局优化算法，具有很强的寻优能力，文献[11]将其与模糊推理结合，得到更优化的系统。但在文献[11]中，由于滤波方法采用的是传统卡尔曼滤波，虽然引入了遗传模糊推理，但是受到传统卡尔曼滤波的限制，在解决严重非线性问题时仍然会带来很大误差。另外，在其模糊推理过程中将系统量测噪声协方差阵R看作一个整体，忽略了R阵内部各个元素之间的差异。为此，本文提出一种基于遗传模糊推理的自适应UKF算法，并将其应用到飞行器的姿态测量中。实验结果表明，与传统的UKF相比，本文所提算法对于噪声统计特性变化时有较强的自适应性，滤波精度也能满足要求。

1 标准无迹卡尔曼滤波

对于如下非线性系统：

(1)

式中：xk为系统状态量；zk为系统观测量；系统过程噪声wk和观测噪声vk均为互不相关的高斯白噪声，协方差分别为Qk和Rk。

无迹卡尔曼滤波具体实现步骤可总结如下：

1)状态初始化

(2)

2)选择UT变换中Sigma点采样策略

(4)

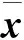
3)时间更新

γi,k|k-1=fk-1(ξi,k-1)

(5)

(6)

(7)

4)量测更新

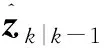
zi,k|k-1=hk(ξi,k|k-1)

(8)

(9)

(10)

(11)

5)状态更新

在获得新的量测zk后，进行滤波状态更新：

(12)

(13)

(14)

由上述UKF算法实现步骤可知，在滤波迭代的过程中，其噪声统计特性都是先验确定的，并且，在整个滤波过程中是保持不变的。而在实际过程中，周围环境以及飞行器的运动状态都是时刻发生变化的。这种基于不变噪声统计特性的标准UKF算法由于不能反映这些变化，所以其滤波精度将受到很大影响，甚至出现发散的现象。因此，需要一种具有自适应容错能力的姿态测量滤波算法。

2 模糊自适应UKF设计

在上一节描述的标准UKF中，假定系统噪声wk和量测噪声vk为零均值，且方差Q和R为已知。通常可以根据反复实验精确获得系统噪声的统计特性，但是量测噪声的统计特性难以通过实验方法精确获得，因为量测噪声随着环境和运动状态的变化而变化。因此可以利用量测信息实时调整量测噪声的统计特性，实现对系统状态的精确估计。

通过卡尔曼滤波的原理可知，假如系统模型足够精确，则残差序列应该为零均值的白噪声，残差方差的实测值与卡尔曼滤波得到的理论值应该接近。如果相差比较大，那么说明量测噪声已经发生变化，需要对量测噪声协方差阵R进行调整，使残差方差的实测值与卡尔曼滤波得到的理论值保持一致。根据这一思路，模糊自适应UKF算法在标准UKF迭代过程的基础上加入如下项：

Rk=FkRk-1

(15)

式中，Fk为维数与Rk相同的对角矩阵，其内部元素的取值由模糊推理系统得到。该模糊推理系统的输入为每一次迭代过程残差的实测方差与理论方差的差值及差值的变化率。定义残差实测方差值为Cz，残差理论方差值为Pz，则：

(16)

(17)

式中，ri为新息序列，也称残差序列，其定义为：

ri=Zi-hk(ξi,k|k-1)

(18)

式中，Cz为最新的N个残差向量的平均值，i0=K-N+1,N表示开窗的大小，视具体情况而定。定义残差的实测方差与理论方差的差值为Ek，即：

Ek=Cz-Pz

(19)

由上述定义可知，通过调整Rk的大小来调整Ek，使之取值在0附近。将每次经过模糊推理运算得到的Fk阵代入式(15)即可进行自适应UKF的计算。

3 遗传模糊推理系统

由第2节提出的模糊自适应UKF算法分析可知，对于该模糊推理系统而言，其输入与输出已知，可以通过多次试验总结以及先验知识，明确地得到其模糊规则。因此，只需要应用遗传算法对该模糊推理系统的隶属度函数进行优化即可。这里，模糊推理系统的隶属度函数选用常用的三角形函数，其中三角形的顶点坐标可以通过先验知识确定，因此通过遗传算法优化的参数主要是三角形的左右下标。遗传算法的具体设定如下：

1)初始种群产生

初始种群随机产生，设定种群规模为100，最大遗传代数为500,并以此作为算法的停止准则。

2)编码

由于实数编码具有精度高、便于大空间搜索、运算简单的特点，特别适合于实际优化问题，所以这里采用实数编码方式，取值范围为[0,1]，编码总长度为8。

3)适值函数

适值函数可以根据飞行器姿态角的均方根误差设计如下：

(20)

式中，m为矢量维数，n为滤波次数，erms为每次滤波后姿态角均方根误差组成的矢量元素。

4)遗传运算

选择操作选择轮盘赌法，即基于适应度比例的选择策略，即个体适应度越高，被选中的概率越大。由于个体采用实数编码，所以交叉操作采用实数交叉法，第k个染色体ak和第l个染色体al在j位的交叉操作方法为：

akj=aij(1-b)+aljb

alj=alj(1-b)+akjb

(21)

变异操作从种群中随机选取一个个体，选择个体中的一点进行变异，以产生更优秀的个体。第i个个体的第j个基因aij进行变异的操作方法为：

(22)

式中，amax是基因aij的上界；amin是基因aij的下界；r为[0,1]区间的随机数；f(g)=r2(1-g/Gmax)2，r2是一个随机数，g是当前迭代次数，Gmax是最大进化次数。

4 实验与结果分析

以陀螺仪、加速度计和磁强计组合测姿系统为应用平台，采用修正罗德里格参数为姿态描述方式，状态量取

(23)

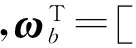
选择重力场和地磁场2个矢量为观测矢量。导航坐标系一般采用北、东、地坐标系，在此坐标系下，重力矢量为固定值A=[0,0,g]T，地磁场矢量可实际测得为M=[HcosI,0,HsinI]T(g为当地重力加

速度，H为磁场强度，I为当地磁倾角)。此时基于重力/地磁的姿态估计系统观测方程为：

Z=C[A,M]T+Vk

(24)

式中：矩阵Z为系统输出矩阵，矩阵C为坐标变换矩阵，可由状态量求出；矩阵Vk为观测噪声。

由于重力场和地磁场2个矢量分别由三维加速度计和三维磁强计测量得出，考虑到加速度计与磁强计内部三个维度特性相近而2个传感器之间的特性不同，所以式(15)中系数阵Fk中元素可作如下简化：

(25)

式中：Fka为反映加速度计特性的量测噪声协方差阵系数，Fkm为反映磁强计特性的量测噪声协方差阵系数。

首先利用该测姿系统在正常工作状态下的数据和遗传算法对模糊推理系统的参数进行离线优化。遗传算法优化500代得到的进化过程如图1所示，经过优化后系统的输入、输出隶属度函数如图2所示。

图1 适应度值变化图

图2 优化后的隶属度函数

为了验证上述算法对环境变化的自适应效果，将组合测姿系统置于转台进行实际测试。一共采集240s的数据，其中前100s实验条件理想，即将转台随机静置于某一角度，计算组合测姿系统输出与转台所置角度偏差；从121s时刻给转台随机加入振动干扰，从而改变环境的噪声统计特性，此时再计算组合测姿系统输出与转台所置角度偏差。为了使实验结果直观明了，特利用式(26)将系统输出由修正罗德里格参数转换为欧拉角进行显示。

(26)

式中：φ,θ和γ分别表示俯仰角、滚转角和航向角。

以俯仰通道为例，对比采用文中上述算法与常规UKF的俯仰角误差，结果如图3所示。

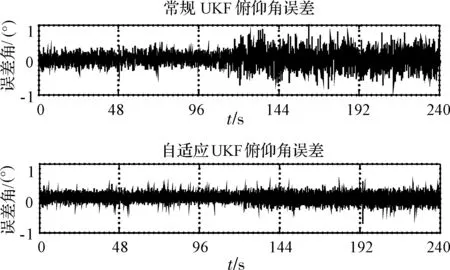
图3 姿态角误差

从图3可以看出，在对量测噪声统计特性估计比较准确的情况下，遗传模糊推理自适应UKF和常规UKF具有相近的精度，但从121s以后噪声发生变化，在对量测噪声估计不准确的情况下，采用遗传模糊推理自适应UKF的精度几乎不受影响，基本稳定在0.5°以内；而采用常规UKF的精度出现恶化，测量误差接近甚至超过1°。对于不确定性变化因素,基于遗传模糊推理的自适应UKF比常规UKF具有更强的自适应能力，也更贴近工程实际应用。

5 结论

针对常规UKF自适应能力不足的问题，首先设计了基于模糊推理的自适应UKF滤波方案；然后利用遗传算法对所设计的模糊推理系统隶属度函数进行离线优化，以提高系统输出精度；最后以陀螺仪、加速度计和磁强计组合测姿系统为平台进行了实际测试，结果表明基于遗传模糊推理的自适应UKF能够满足测量精度，且比常规UKF有更强的自适应能力。由于系统所用的ARM处理器计算能力有限，遗传算法对参数进行优化是通过采集几组比较理想的传感器数据在Matlab软件中离线进行的，这样无疑会对优化的参数造成一定影响。如果采用运算更快的处理器进行在线优化，优化效果会更好。

[1] 赵琳,王小旭,李亮,等.非线性系统滤波理论[M].北京：国防工业出版社,2012:68-108.

[2] 李鹏,宋申民,段广仁.改进的平方根UKF及其在交会对接中的应用[J].电机与控制学报,2010,14(11):100-104.(Li Peng, Song Shenmin, Duan Guangren. Improved Square Root Unscented Kalman Filter and Its Aapplication in Rendezvous and Docking[J]. Electric Machines and Control,2010,14(11):100-104.)

[3] 黄琳.非线性滤波理论在航天器姿态确定中的应用[D].哈尔滨: 哈尔滨工业大学, 2007.(Huang Lin. Applications of Nonlinear Bayesian Filtering Algorithms to Spacecraft Attitude Determination[D].Harbin: Harbin Institute of Technology,2007.)

[4] 计会凤,徐爱功.相关法自适应滤波在动态行程时间预测中的应用研究[J]. 测绘科学,2010,35(2):158-160.(Ji Huifeng,Xu Aigong. The Feasibility Analysis of the Relevant Adaptive Filtering in the Dynamic Travel Time Prediction[J].Science of Surveying and Mapping,2010,35(2):158-160.)

[5] 石静,缪玲娟,倪茂林.一种抗野值自适应滤波算法及在MEMS-SINS/GPS中应用[J].宇航学报,2010,31(12):2711-2716.(Shi Jing, Miao Lingjuan, Ni Maolin. An Outlier Rejecting and Adaptive Filter Algorithm Applied in MEM S-SINS/GPS [J]. Journal of Astronautic, 2010,31(12):2711-2716.)

[6] 胡健,马大为,周百令.快速传递对准用联合强跟踪Kalman滤波器设计与仿真[J].中国惯性技术学报,2010,18(1):48-57.(Hu Jian, Ma Da-wei, Zhou Bai-ling. Design and Simulation of Federated Strong Tracking Filter for Rapid Transfer Alignment[J]. Journal of Chinese Inertial Technology,2010,18(1):48-57.)

[7] GAO Weixi, MIAO Lingjuan, NI Maolin. Multiple Fading Factors Kalman Filter for SINS Static Alignment Application[J]. Chinese Journal of Aeronautics,2011,24(4):476-483.

[8] 张圆,郭晨,谢春思,等.基于模糊神经网络融合的目标自适应跟踪算法[J].大连海事大学学报,2007,33(2):120-123.(Zhang Yuan,Guo Chen,Xie Chunsi,et al. Adaptive Algorithm in Target-tracking Based on Fuzzy Neural Networks Information Fusion[J]. Journal of Dalian Maritime University,2007,33(2):120-123.)

[9] 王玲玲,富立.模糊推理在捷联航姿系统中的应用[J].中国惯性技术学报,2006,14(6):45-47.(Wang Lingling, Fu Li. Application of Fuzzy Reasoning in Strapdown AHRS[J]. Journal of Chinese Inertial Technology, 2006,14(6):45-47.)

[10] 汪定伟,王俊伟,王洪峰,等.智能优化方法[M].北京:高等教育出版社,2007:21-50.

[11] 高运广,王仕成,刘志国,等.一种基于遗传模糊推理的自适应容错滤波算法[J].中国惯性技术学报,2012,20(3):315-319.(Gao Yunguang, Wang Shi-cheng, Liu ZhiGuo,et al. Adaptive Fault Tolerant Tilter Method Based on Fuzzy Inference System Optimized by Genetic Algorithm[J]. Journal of Chinese Inertial Technology,2012,20(3):315-319.)

Adaptive UKF for Integrated Attitude Measuring Based on Fuzzy Inference System Optimized by Genetic Algorithm

XIAO Wenjian LU Ping

Department of Unmanned Aerial Vehicle Engineering Ordnance Engineering College, Shijiazhuang 050003, China

FortheshortageofstandardUKFforadaptivityinintegratedmeasuringattitude,anadaptiveUKFmethodbasedonfuzzyinferencesystemoptimizedbygeneticalgorithmisproposed.Firstly,theadaptiveUKFbasedonfuzzyinferencesystemisbuilt,whichadjuststhemeasurenoisetoestimatethesystemstatusaccurately.Secondly,thegeneticalgorithmisappliedtotheparametersoptimizationofmembershipfunctionofflineinordertoimprovetheaccuracyofsystem.Finally,theexperimentbasedonattitudemeasuringsystemcomprisedbygyro,accelerometerandmagnetometerisdemonstrated.TheexperimentshowstheadaptiveUKFbasedonfuzzyinferencesystemcankeepbettermeasurementprecisionwhenthemeasurenoiseischanging.

Integratedattitudemeasurement; UKF;Geneticalgorithm;Fuzzyinference;Adaptive

2013-04-08

肖文健(1989-)，男，河北张家口人，硕士研究生，主要研究方向为导航、制导与控制；路 平(1961-)，男，石家庄人，教授，主要研究方向为无人机通信链路与导航。

U666.1

A

1006-3242(2013)05-0035-06