气体分馏装置多变量预测函数控制方法

仇文爽， 李 平， 曹江涛， 苏成利

(辽宁石油化工大学信息与控制工程学院，辽宁抚顺113001)

脱丙烷塔是炼油厂气体分馏装置和化工厂气体分馏装置中重要的操作单元，其主要目的就是实现碳三和碳四的分离，它的分离程度直接影响后续异丁烯塔的控制操作，从而影响最终的产品质量，所以脱丙烷塔的过程控制尤为重要。与其他石油化工生产过程一样，脱丙烷塔的实际生产过程存在着以下特点:(1)大规模连续生产，各变量之间存在着不同程度的耦合;(2)系统的动态响应复杂及所存在的大滞后过程。所以说影响装置稳定的干扰因素多，常规控制很难保证在工况变化时仍有较好的控制性能，导致装置运行的稳定性差，影响产品的质量和产量;再加上脱丙烷塔一般由多级塔板组成，塔的内在机理复杂、动态响应慢、控制回路关联性强、控制过程十分复杂。当生产过程中出现工况改变时，采用常规控制，难以达到理想的控制效果，而采用预测函数控制可以在很大程度上解决上述问题，改善或进一步优化常规控制。

预测函数控制方法是由Richalet等人提出的一种新型预测控制算法。它与传统的预测控制算法最大的不同在于引入基函数概念使系统的输入结构化。传统的预测函数控制故能把复杂的系统控制好，但是要达到很好的动态性能，必须对算法进行改进。目前已有许多对于预测函数控制算法的改进，如文献［1］提出一种基于单步的预测输出差值抑制超调的改进的预测控制算法，解决了系统响应有超调和跟踪慢的问题;文献［2］提出了一种基于期望响应的预测函数控制参考轨迹自校正方法，能够使系统响应准确跟踪期望轨迹。

实际工业过程往往希望工艺参数的动态响应能够很快地跟踪期望的设定值，达到好的控制效果。改进的预测函数控制算法基本都是改善系统的3个性能指标，使系统达到更好的控制效果。文中针对脱丙烷塔大时滞、强耦合特性系统的动态响应慢的问题，采用多变量预测函数控制算法，针对快速性这一性能指标进行改进并兼顾稳定性及准确性，提出一种由原来预测时域固定的变为预测时域可调的多变量预测函数控制算法，这种算法能够改善系统的快速性，优化系统的动态特性。

1 多变量预测函数控制算法

1.1 多变量预测函数控制算法推导

预测函数控制是预测控制的一种，它也有模型预测的3个主要特征:预测模型，反馈校正，滚动优化。它与传统的预测控制的主要区别在于，预测函数控制的输入是事先选定的若干基函数的线性组合，比较结构化［3］。通常所说的预测函数算法是单变量的，对于工业过程中来说，绝大部分被控对象是多变量系统。因此为使该算法应用到工业过程中有必要推导多变量的预测函数控制算法。下面以三输入三输出为例推导算法［4］。

1.1.1 预测模型

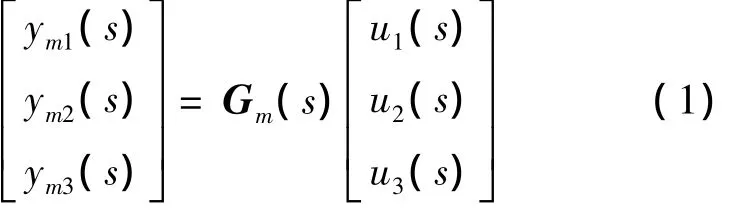
其中uj(s)，ymj(s)分别为预测模型第j(j=1，2，3)个输入和输出，传递函数表达式Gm(s)如式(2)所示:

其中Kmij，Tmij，τij(i，j=1，2，3)为预测模型的稳态增益、时间常数和纯滞后时间。

为推导一阶加纯滞后系统的控制量，要根据Smith预估的思想［5］先推导去掉滞后环节系统的多变量预测函数控制算法，然后根据得到控制量表达式对控制量进行修正。选取单位阶跃函数为基函数，控制量输入为

其中uj(j=1，2，3)为第j个控制输入的基函数的线性组合系数，uj(k+i)为第j个控制输入在k+i时刻的值。

1.1.2 误差预测及补偿 预测函数控制算法误差的预测及补偿由两部分组成，其中一部分是系统误差，它是由模型失配及外界干扰产生的误差;另一部分是固有误差，是由系统本身存在滞后所造成。针对系统误差，3个被控变量的优化时域取相同值，即P1=P2=P3=P，则误差补偿后的预测模型输出为

其中ej(k+P)，ymj(k+P)，k+P)分别为k+P时刻的系统误差、模型输出以及误差补偿后的模型输出。系统误差ej(k+P)为

y'mj(k)为k时刻无滞后环节的模型输出，ypj(k)为补偿前系统实际输出。针对系统固有误差，采用Smith预估思想对系统的输出进行修正，修正方法如下:

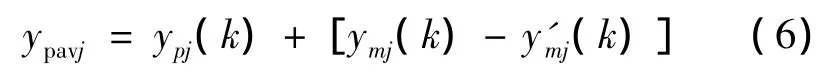
其中ymj(k)为k时刻有滞后的模型预测输出，ypavj为Smith补偿后系统实际输出。

1.1.3 优化计算 参考轨迹采用常见的一阶指数形式，则k+P时刻的参考轨迹为

其中 λj=e－Ts/Ttj，Tj为系统的采样时间，Trj为参考轨迹的响应时间，yrj(k+P)为k+P时刻的参考轨迹，cj(k)，cj(k+P)分别为k时刻、k+P时刻的设定值，yp(k)为k时刻过程的实际输出值。在系统误差补偿的前提下，算法的优化指标为

其中n为输出变量的个数，文中选择三输入三输出系统，因此n=3。

无滞后环节时，由式(4)，(5)，(7)，(8)经过推导，得到的控制量为

有滞后环节时，由式(4)，(6)，(7)，(8)经过推导，得到的控制量为

1.2 多变量预测函数控制算法的改进

考虑到预测函数控制算法的滚动优化的柔化控制的目的，不是使输出直接跟踪设定值，而是跟踪参考轨迹，故参考轨迹各项参数的选取尤为重要，而预测优化时域P对稳定性和鲁棒性起主要作用［6］。

文献［7］中提到Blocking技术，Blocking技术打破了预测控制和控制时域连续时刻取点的传统思想，采用离散不等间隔的选取方法设置预测时域。该文献对Blocking技术的研究，提出了可变控制策略的方法。根据控制策略的特性，在不同输出状态，采用不同的控制策略［7］。文献［8］中使用的方法是参考轨迹在线自动跟踪被控变量输出，使预测控制针对输出在不同区域范围内采取不同的控制强度，从而实现平稳控制［8］。

文中根据系统的输出量大小，在输出量各阶段采用不同的预测时域，在线改变跟踪参考轨迹的快慢，从而使输出能够快速地跟踪期望的轨迹，减小了调节时间，且兼顾了系统的稳定性和鲁棒性。具体作法是在输出y不同时段即把y分成以下10段［9］:0% ～ 10%，10% ～ 20%，20% ～ 30%，30% ～40%，40% ～50%，50% ～ 60%，60% ～70%，70% ～80%，80% ～90%，90% ～100%，每段的λj指数P有不同的取值，而不是选取固定的一个值，这样就保证输出不同阶段采取不同的控制强度，能够使输出快速跟踪期望值，优化了系统的动态特性。

2 脱丙烷塔的工艺流程及建模

脱丙烷塔是炼油厂气体分馏装置和化工厂气体分馏装置中重要的操作单元，其主要目的就是实现碳三和碳四的分离。

图1 为气体分馏装置中脱丙烷塔的流程简图。

图1 脱丙烷塔工艺流程Fig.1 Process flow diagram of depropanizer

工艺流程如下:液化气水洗后，经脱丙烷塔进料泵送往脱丙烷塔进料预热器，经蒸汽冷凝水预热到70℃ 左右，进入脱丙烷塔，脱丙烷塔塔底重沸器采用0.8 MPa蒸汽加热。碳三馏份从塔顶馏出，经空气冷凝器冷凝冷却至35℃流入脱丙烷塔回流罐，回流罐中的冷凝液经脱丙烷塔回流泵一部分打回流入塔，一部分作为成品出装置去液化气贮运装置或聚丙烯装置，而碳四馏份从塔底馏出，这样就实现了C3和C4的分离。

为了顺利进行脱丙烷塔的先进控制，首先对装置进行深入细致的现场调研，了解清楚该装置的运行情况，运用流程模拟软件PRO/II对该脱丙烷塔的现状进行流程模拟［10］，找到该塔优化运行的指导性操作参数。通过搭建先进控制系统硬件平台，完成先进控制的上位机与DCS系统OPC通信，实现了数据采集功能。并对各控制回路的PID控制器参数进行重新整定。在此基础上，运用基于阶跃响应的系统辨识方法［11］，现场进行阶跃模型测试。整个测试过程应满足以下条件:(1)保证装置特性的相对稳定，能够反映正常生产情况;(2)各种工艺设备处于良好状态;(3)各种仪表以及常规控制系统状态良好;(4)DCS数据采集系统工作正常，所要测试的过程变量必须由先进控制上位机的数据采集系统采集并存储;(5)所有可投自动控制回路已设法投自动，且过程相对平稳。

测试过程:(1)每一个操作变量以及干扰变量做2～3次正负阶跃改变以测试重复性;(2)按组对操作变量及干扰变量进行测试，做到边测试边分析;(3)每一次阶跃改变应专心于一个被控变量的改变;(4)测试过程中，如果遇到各种不可预测干扰的影响，应作详细的记录，以便为模型辨识之前剔除坏数据提供依据;(5)对不满意的测试结果，应进行更多的阶跃测试，直到获得满意的响应为止。

经过阶跃测试后进行数据拟合得到脱丙烷塔的数学模型(如式(11))。该模型是三输入三输出系统，3个被控变量分别是:塔顶温度，灵敏板温度，塔底液位。3个操作变量分别是:回流量设定，蒸汽流量设定，塔底采出量设定。各变量之间存在强耦合。

3 算法验证

为了验证算法的有效性，选取某石化公司气体分馏装置的脱丙烷塔作为被控对象。

多变量预测函数控制(MPFC)的控制参数如下:采样周期为50 s，参考轨迹柔化系数为0.01，固定的预测时域为55步。为了达到更好的动态效果，用改进的预测函数控制算法对系统进行控制。采样周期及参考轨迹柔化系数不变，预测步数由原来固定步数改为可调的。具体预测步数设定如下:塔顶温度的预测步数在输出y值的各段预测步数分别为35，38，37，38，35，36，38，40，50，60 步。改进的 MPFC与MPFC算法仿真比较结果如图2所示。

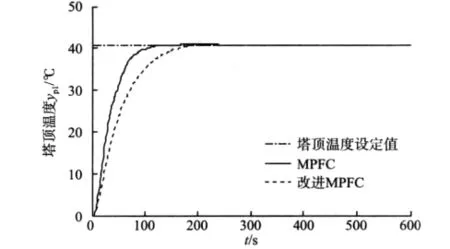
图2 改进MPFC与MPFC仿真比较Fig.2 Simulation comparison between modified MPFC and MPFC

灵敏板温度的预测步数在输出y值的各段预测步数分别为 35，35，35，38，35，36，38，35，35，38 步。改进的MPFC与原MPFC算法仿真比较结果如图3所示。

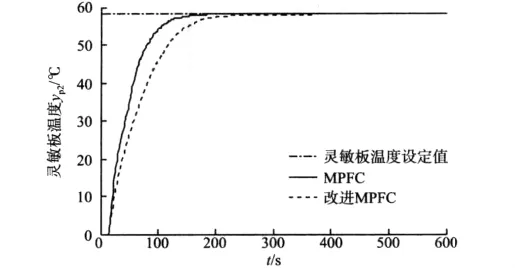
图3 改进MPFC与MPFC仿真比较Fig.3 Simulation comparison between modified MPFC and MPFC

塔底液位的预测步数在输出y值的各段预测步数分别为 35，35，35，38，35，36，38，35，35，38 步。改进MPFC与原MPFC算法仿真比较结果如图4所示。从仿真结果可以看出，预测时域可调的控制算法比预测时域固定的控制算法的调节时间变短，跟踪速度变快。

图4 改进MPFC与MPFC控制算法仿真比较Fig.4 Simulation comparison between modified MPFC and MPFC

当系统工况改变时，如在800 s时塔底液位设定值由原来的60%变为68%，改进的控制算法不仅有较强的鲁棒性，而且能加快各被控变量跟踪设定值的速度。塔顶温度、灵敏板温度、塔底液位在工况改变后改进的MPFC与MPFC算法仿真比较结果分别如图5～7所示。

仿真结果表明，当塔底液位设定值改变后塔顶温度及灵敏板温度有一定范围的波动，说明系统各变量之间存在强耦合特性，但是很快又跟踪上设定值，所受工况改变的影响较小，由此也表明预测函数控制算法的鲁棒性比较好。而且改进的MPFC比原MPFC的调节时间短，改善了系统的动态特性。为了说明调节时间长短列表说明，如表1，2所示。

表1 改进MPFC与MPFC的调节时间Tab.1 Regulation time of modified MPFC and MPFC

表2 工况改变后改进MPFC与MPFC的调节时间Tab.2 Regulation time of modified MPFC and MPFC after changing working conditions

从表1，2中可以看出，塔顶温度、灵敏板温度、塔底液位三者在预测时域可调时的调节时间要比预测时域固定时的调节时间短，说明改进后的算法能加快反应速度，改善系统的动态性能。为不失一般性，在800 s时塔顶温度设定值由原来的40.9℃变为38℃，进行Matlab仿真，塔顶温度、灵敏板温度、塔底液位在工况改变后改进的MPFC与MPFC算法仿真比较结果分别如图8～10所示。

从图8～10仿真中可以看出，在800 s塔顶温度设定值由原来的40.9℃变为38℃时，改进的多变量预测函数控制算法比原始算法灵敏板温度和塔底液位能够很快地回到期望值，调节时间变短。

通过工况改变后Matlab的仿真可以看出，改进的算法工况改变对被控变量的影响比原算法小，能很快回到期望值，鲁棒性高。

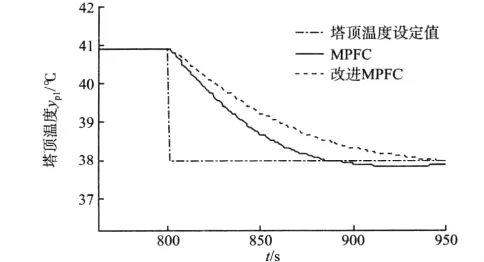
图8 工况改变后改进MPFC与MPFC算法仿真比较Fig.8 Simulation comparison between modified MPFC and MPFC after changing working conditions

图9 工况改变后改进MPFC与MPFC算法仿真比较Fig.9 Simulation comparison between modified MPFC and MPFC after changing working conditions

4 结语

文中主要研究了多变量预测函数控制算法及其改进算法，并且对脱丙烷塔这种大滞后、强耦合、多变量系统进行了Matlab仿真。

图10 工况改变后改进MPFC与MPFC算法仿真比较Fig.10 Simulation comparison between modified MPFC and MPFC after changing working conditions

改进的预测函数控制算法打破了传统预测函数控制算法预测时域固定的思想，把预测时域变为可以根据系统预测输出大小进行分段可调，将改进的算法与原算法应用到气体分馏装置的脱丙烷塔中，通过Matlab仿真，结果表明改进的预测函数控制算法通过对预测时域进行分段设定，与原算法相比，不仅能够使系统加快反应速度使调节时间变短，而且能够使脱丙烷塔在某一被控变量设定值改变后其他被控变量能够很快回到期望值，说明改进的预测函数控制算法具有较强的鲁棒性，改善了系统的动态性能。

［1］戴文战，田仕军，杨爱萍.基于单步预测输出差值抑制超调的改进的预测控制算法［J］.东南大学学报，2011，44(增):1-4.DAI Wen-zhan，TIAN Shi-jun，YANG Ai-ping.An improved predictive control algorithm based on single-step predictive output difference for restraining overshoot［J］.Journal of Southeast University，2011，44(Sup.):1-4.(in Chinese)

［2］沈国良，赵均，钱积新.基于期望响应的预测函数控制参考轨迹自校正方法［J］.化工学报，2008，59(1):119-125.SHEN Guo-liang，ZHAO Jun，QIAN Ji-xin.Self-tuning scheme of predictive function control’s reference trajectory based on expected response［J］.Journal of Chemical Industry and Engineering，2008，59(1):119-125.(in Chinese)

［3］张泉灵.预测函数控制及应用研究［D］.杭州:浙江大学，1999.

［4］宁璀，张泉灵，苏宏业.多变量一阶加纯滞后系统的预测函数控制［J］.信息与控制，2007，36(6):702-707.NING Cui，ZHANG Quan-ling，SU Hong-ye.Predictive functional control for multivariable first order plus dead time system［J］.Information and Control，2007，36(6):702-707.(in Chinese)

［5］Smith O J M.Closer control of loops with dead time［J］.Chemical Engineering Progress，1957，53(5):217-219.

［6］王治祥.变参考轨迹系数模型算法控制［J］.武汉工业大学报，1992，14(2):85-89.WANG Zhi-xiang.Variable reference trajectory coefficient of model control algorithm［J］.Journal of Wuhan University of Technology，1992，14(2):85-89.(in Chinese)

［7］朱娜娜.模型预测控制简化算法的研究［D］.杭州:浙江大学，2011.

［8］罗雄麟，周晓龙，朱丽萍.参考轨迹在线优化的区间预测控制［J］.控制工程，2013(2):223-226.LUO Xiong-lin，ZHOU Xiao-long，ZHU Li-ping.Zone model predictive control with online optimization of reference trajectory［J］.Control Engineering of China，2013(2):223-226.(in Chinese)

［9］李润德，薛云灿.参考轨迹系数可变的模型算法控制(基础研究)［J］.河海大学机械学院学报，1995，9(1):33-38.LI Run-de，XUE Yun-can.Reference trajectory coefficient variable model algorithmic control(basic research)［J］.Journal of College of Mech Eng Hohai University，1995，9(1):33-38.(in Chinese)

［10］刘宗林，苏成利，李平.气体分流装置脱丙烷塔的流程模拟［J］.化工自动化仪表，2011(10):1254-1256.LIU Zong-lin，SU Cheng-li，LI Ping.Depropanizer simulation analysis in gas fractionation unit［J］.Control and Instruments in Chemical Industry，2011(10):1254-1256.(in Chinese)

［11］齐臣坤，李少远.基于阶跃响应测试的过程控制系统辨识与应用［D］.上海:上海交通大学，2004.