基于虚拟支点倒立摆模型的双足机器人质心轨迹规划
2013-08-16赵九洲居鹤华
赵九洲, 居鹤华, 王 恒
(北京工业大学深空机器人研究中心,北京100024)
人类的直立行走是一种能效很高的运动,相比四足运动与其他步行方式,直立行走可以节省大约75% 的能量[1]。目前,大部分基于主动行走方式的仿人机器人远达不到这一效率,因此很多学者转而研究被动步行领域,并取得了一定的成果[2-3]。但是,这种方式与主动方式相比机器人的稳定性和灵活性很差。如何将这两个方面的成果有机结合,进而在保证稳定性和灵活性的前提下实现与人类接近的能耗是当前的研究热点。
很多学者认为导致主动方式能耗过高的主要原因是驱动方式不符合人类的生物力学特性[4],但这只是部分原因,步行模式与抗扰性策略也是影响步行能效的两大因素。
文中主要探讨步行模式与能效的关系,从传统的线性倒立摆步行模型与被动步行的原理出发,以期找到一种可以有效结合这两种方式各自优点的替代方案用于主动步行机器人。
1 线性倒立摆规划方法分析
基于线性倒立摆模型与质量小车模型的步行规划方法是目前最为成熟的规划方法,这两种方法本质上是一致的,很多著名仿人机器人均采用这种方法,如 ASIMO,HRP,P1 等[4]。为了研究双足机器人的能耗特性,首先分析线性倒立摆的运动特点。
需要注意的是,采用简化模型的前提是保证运动绕质心的角动量近似守恒[4],此时才能保证零力矩点(Zero Moment Point,ZMP)与倒立摆的支点一致,这与实际工程需要和人类的正常步行中的情况很接近。
1.1 线性倒立摆的数学模型及运动特性
线性倒立摆的基本原理如图1所示。

图1 线性倒立摆模型Fig.1 Linear inverted pendulum model
图1 中伸缩杆产生的作用力f竖直方向上的分量恰好补偿重力,因此质心只沿水平方向运动,自由度可以由水平位移x表示,由此推出线性倒立摆的动力学方程为

由于z0不变,因此可以解出x轨迹为

其中,sh()与ch()表示双曲正弦 /余弦,进一步可以求得系统从一个状态到另一个状态的过渡时间
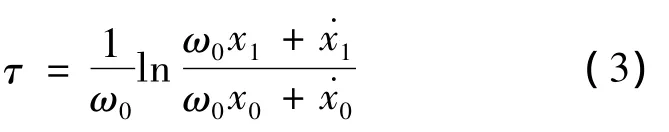
线性倒立摆需要满足一定的初值条件才能从初始位置摆过支点的正上方,对应的机器人才能成功地迈到下一步,这个特性称为轨道能量特性[4](线性倒立摆的轨道能量是恒定的)。当初速度不够或者初始位置离平衡点过远时,质点未到达支点上方动能就下降为0,此时就无法摆过平衡点。具体而言,就是要求轨道能量E大于0,即

1.2 基于线性倒立摆的规划方法
机器人的步行规划需要满足两个条件:①保证质心能够从初始位置出发顺利过渡到下一步的初始位置;②保证脚掌的压力中心点在这一过程中能够基本保持在支撑凸多边形中,从而保证机器人不会沿着多边形边缘进行非预期的翻转[5]。压力中心也称零力矩点,其定义、原理以及计算与测量方法见文献[6]。
当为机器人设定了步长S与步行周期TS后,可以很容易利用线性倒立摆的特性及对称性原则对机器人的质心轨迹进行规划,同时满足上面的两个条件。
线性倒立摆规划方法如图2所示。

图2 线性倒立摆规划方法Fig.2 Linear inverted pendulum planing method
根据对称性原则,倒立摆在步行周期开始和结束时刻的位置为-S/2和S/2,初始和结束时刻的速度相等,根据式(3)可求出:
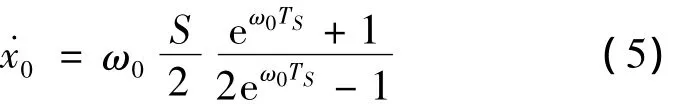
将求得的速度与半步长作为初始条件求得如图3所示的质心位置与速度轨迹。

图3 线性倒立摆规划轨迹Fig.3 COM trajectory by LIP planing method
由图3可以看出,当质心位于支点正上方时,速度达到最小值,此时系统的机械能最小;而后,系统逐渐加速,直到与初速度相同。
1.3 线性倒立摆的能量特性分析
由式(1)可以看出,质心的加速度与位置是成正比的,这是一个典型的正反馈系统,因而不能用被动的弹簧阻尼系统进行等效,所以它的机械能不守恒。其机械能曲线如图4所示。

图4 线性倒立摆的机械能曲线Fig.4 Mechanical energy of LIP
由式(4)可以求出系统在初始时刻与周期中点之间的动能差
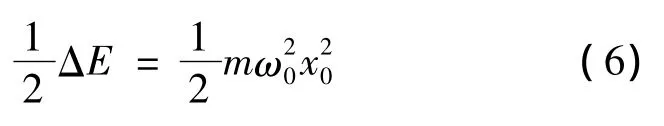
伸缩杆的正反馈特性使其在这一过程中无法储存能量,因此需要从驱动器获取的能量实际为式(6)的2倍。
考虑无量纲能量:

可以求出,这一过程中需要输入的无量纲化能量为

可以看出,输入能量是和步长与质心高度的比值成正比,当步长相对于质心高度越大,损失能量也就越多。
反观人类的步行方式,会发现人类在行走过程中其质心高度是起伏不断的[7],具体如图5所示。

图5 人类自然步态Fig.5 Natural gait of human
在单腿支撑相类似于一个固定杆长的被动倒立摆,在摆动过程中,动能转化为重力势能以保证满足步行规划的2个基本条件。其机械能是近似守恒的,这样质心在摆动过程中需要输入的能量近似为零,所以人类的步行模式效率要远高于线性倒立摆规划出的步态。
2 虚拟支点倒立摆规划方法
人类在单腿支撑相的运动轨迹类似于近似被动特性的倒立摆的运动,若将其应用到主动步行的双足机器人上面,这样既可以得到与人类接近的步态与效率,又可以应用主动步行领域取得的成果。
2.1 被动倒立摆的数学模型及运动特性
被动倒立摆的基本原理如图6所示。
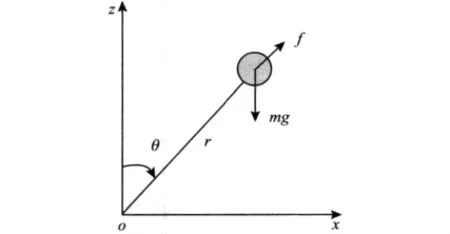
图6 被动倒立摆的模型Fig.6 Passive inverted pendulum model
由图6可以看出,在运动过程中,支撑杆的长度是固定的,因此质点在重力与支撑力的作用下进行变速圆周运动,由于质点的高度不是固定的,因此不能用x坐标作为系统的自由度,取z轴转到支杆之间的角度作为系统的自由度。
在运动过程中,重力对于支点产生一个力矩,而支撑力对支点的力矩为0,由角动量定理可以推出系统的动力学方程为

该方程与线性倒立摆的动力学方程很接近,尤其是当角度范围在0附近变化不大时。所以,线性倒立摆可以作为机器人步态规划的一个有力工具。
和线性倒立摆类似,质点的初速度也需要满足一定的初始条件才能保证顺利地度过最高点。通过动能定理可以很容易求出这个初始条件:
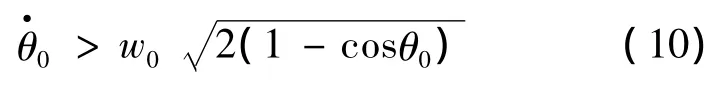
可以证明,根据式(9)所求出的最小值对应的质点速度总是小于由式(4)所求出的速度。
求解式(9)可以得到
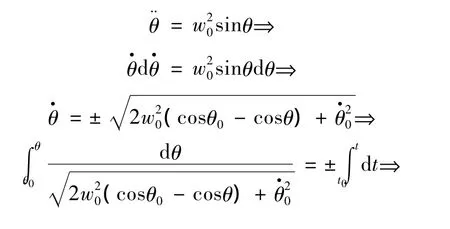
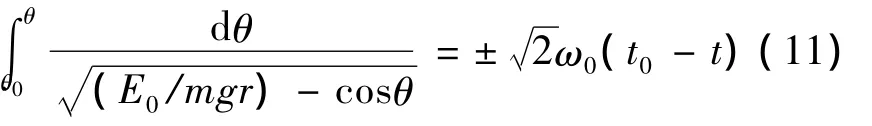
为了摆过支点,初始能量势必大于最高点的势能,因此式(11)等号左边是一个非初等积分,导致这个微分方程没有初等解。利用数值方法可以很容易的求解出这个微分方程的解轨迹,但数值方法求解速度较慢,故采用MATLAB中ODE45方法对其进行求解,结果如图7所示。
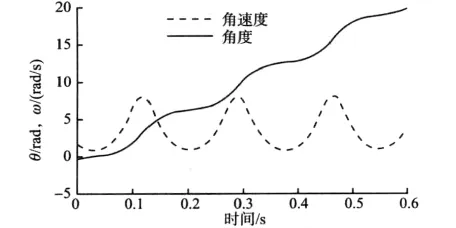
图7 被动倒立摆的解轨迹Fig.7 Solution of PIP
由图7可以看出,这个解轨迹与线性倒立摆的解轨迹在局部(纵轴0点附近)是很接近的,因此可以利用线性倒立摆的某些结论对被动倒立摆进行估算。
2.2 虚拟支点倒立摆模型
在运动过程中,被动倒立摆的机械能是恒定的,与人类的步态类似。然而直接利用被动倒立摆模型进行步行的运动规划时,会遇到一定的困难。
以踝关节作为倒立摆的支点,在摆动过程中保持支撑腿伸直,基于被动行走原理的机器人大多采取这一方式,这是一种最省能量的方式,得到的运动轨迹如图8所示。

图8 直腿规划Fig.8 Straight leg gait planning
由图8可以看出,这种方式得到的ZMP位于支杆的延长线与地面的交点上,在运动过程中,从脚的前部移动到脚跟,这与人类实际步行过程中的ZMP的运动方向正好相反,而且在支撑后期ZMP有可能脱离支撑脚的范围,造成机器人绕脚跟翻转。
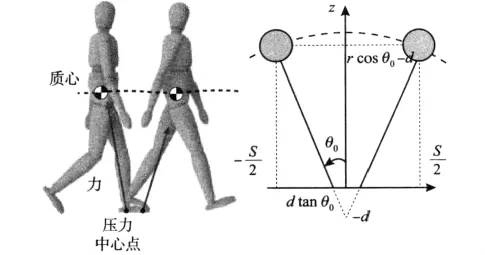
图9 虚拟支点倒立摆模型Fig.9 Virtual pivot inverted pendulum planing model
由此推测,与人类质心轨迹对应的倒立摆并不是绕踝关节旋转的,为了使ZMP曲线更加接近人类步行时的特性,也为了提高稳定性,文中提出了一种虚拟支点倒立摆模型,具体如图9所示。在这种模型中,倒立摆的支点是位于地面之下的一个虚拟点,当质心从起始位置摆动到终止位置时,ZMP点恰好由脚跟移动到前脚掌位置,这与人类实际步行时ZMP点的轨迹十分相似;并且在这一过程中,机械能是近似守恒的。需要注意的是,这种方法求出的运动模式中,膝关节不是完全伸直的,而是近似伸直的,因而这种方法的效率不如直腿规划的效率高,但它的稳定性更好,也更符合人类行走的特点。
同时需要指出的是,人类在单腿支撑阶段的初始位置和结束位置不是完全对称的,人类脚的结构也不是依踝关节前后对称的,甚至人类左步与右步也非完全对称,因此作者认为非对称性规划方式应该作为下一步研究的重点。
2.3 虚拟支点倒立摆运动状态的估计
虚拟支点倒立摆与被动倒立摆的动力学方程是一致的。但这种微分方程式是没有初等解的,因而对于直接利用倒立摆方程求取步行参数造成了一定的困难。
直接利用数值方法求解微分方程虽然可以精确估算出质点的运动状态,但计算效率并不高,而且这种没有解析形式的轨迹也没有便捷的方法估计系统从一个状态过渡到另一个状态的时间。因此,文中希望将线性倒立摆已有的结论应用到倒立摆模型中。
解轨迹与线性倒立摆的解轨迹在局部[0,x]附近是很接近的(x满足令角度在0的值与角度在x的值是一对相反数),这是由于当倒立摆处于0点附近时,有

由式(9)可以推出:

它与式(1)是相同形式的,因此由(2)式可以推出

同时,当给定步行时间与步幅,利用式(5)和式(3),可以推出满足该条件的初始角速度
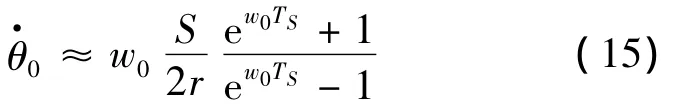
为了验证式(14)的有效性,采用不同过渡时间、初始角度以及摆长的倒立摆模型,分别用ODE45与式(14)中的表达式进行计算,得到的结果如图10~图12所示。


由图10~图12可以看出,只有初始角度的变化对拟合程度的影响最大,当初始角度在20°以内时,采用上述的估算是得到的结果是基本一致的。
对于不同的初始角度,利用式(15)求取的初速度存在一定的偏差;随着初始角度的增大,初速度估算往往偏小,导致不能回到原来的角速度。因此,在实际使用中利用下式估算初始角速度:
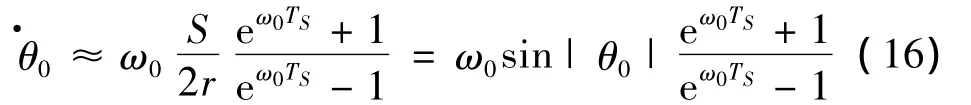
所得结果如图13所示。

图13 倒立摆轨迹估计Fig.13 Estimation of solution of VPIP
由图13可以看出式(14)与式(16)可以比较准确地根据步长与过渡时间估计初速度与角度。
2.4 基于虚拟支点倒立摆模型的双足机器人步行规划方法
当给定了步幅、过渡时间、ZMP在脚掌上的运动范围、质心初始高度后就可以根据平衡性原则计算出虚拟质点倒立摆的初始角度,初始速度以及摆长,进而算出质心轨迹(见图14)。在实际应用中,需要保证质心轨迹满足机器人机构的运动学约束。

图14 虚拟支点倒立摆规划Fig.14 VPIP planning method
可以求出:

由此可以求出质心轨迹为
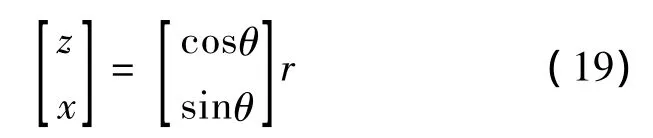
基于虚拟支点倒立摆模型规划出运动,其质心在初始与结束时刻的速度大小相等但方向不同,因此有必要引入双腿支撑阶段以保证速度平滑地从结束时刻过渡到下一个开始时刻。设定双腿过渡时间为td,为简化计算,假设在此过程中竖直方向的速度分量均匀变化,并忽略地面以及腿部的碰撞、缓冲与储能作用,以求取在这一过程中系统最多需要输入多少能量,则时间段的中点恰好为系统机械能最低点。由此可以计算出系统在双腿阶段的初始机械能与中点的机械能之差:

考虑到

总消耗能量为式(20)的2倍,将其无量纲化得

为简化式(22),设

则式(22)可简写为

3 数值仿真
为了验证虚拟支点倒立摆规划出的运动效率,文中选取了一组与人类步态接近的质心高度、步幅、脚长及步行周期,分别比较其相对于采用同样参数的线性倒立摆规划出运动的效率。所选参数见表1,需要注意的是线性倒立摆与虚拟支点倒立摆对应的初始角度是不一致的,为了区别取线性倒立摆的初始角度为φ0。

表1 数值仿真参数Tab.1 Parameters of numerical simulation
根据式(14)可以求出系统的运动方程为

由式(19)可以计算出质心的运动轨迹为

根据2.4中假设,在双腿支撑阶段,有
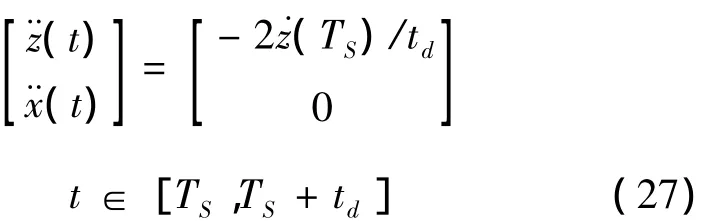
由此可以推出双腿阶段的质心轨迹为

起点值可由步行参数求出,代入后得到:

这样得到一个周期之内的步行质心轨迹,可以看出这个轨迹和人类实际运动时比较符合(见图15)。
质心轨迹确定后,就可以根据逆运动学确定机器人各个关节的角度,用于轨迹跟踪控制。

图15 虚拟支点倒立摆规划出的轨迹Fig.15 COM trajectory by a VPIP planning method
根据式(9)可以求得基于线性倒立摆的运动模式在一步之内至少需要0.138 9的能量,而根据式(24)虚拟支点倒立摆的运动模式在一步内最多需要0.016 3的能量,只有线性倒立摆消耗能量的1/8,因此虚拟支点倒立摆规划方法在该参数下的效率是线性倒立摆的近8倍。
事实上,为了减少机构的负荷,线性倒立摆同样需要引入双腿阶段保证速度的平滑过渡,由此需要输入更多的能量;同时,考虑到人类在双腿阶段地面的非弹性碰撞以及支撑腿与足部的被动弹簧特性,在双腿阶段实际的能量输入远小于式(24)中的结果,因此实际步行中的效率比要更高。
4 结语
文中提出的虚拟支点倒立摆模型能够较好地描述步行时质心曲线、地面反力、被动特性以及能量消耗之间的关系,与人类直立行走时的规律接近;更为重要的是,这一模型符合简单性的原则,在建模的时候,没有复杂的算法以及需要辨识的参数,质心的运动规律主要依赖于倒立摆模型。
仿真结果表明,通过这种规划方法,系统可以节省近7/8的额外输入能量,且得到和人类相似的质心轨迹。需要指出的是,人类的施力方式以及抗扰性策略同样是影响步行效率的两大因素,从这3个方面同时入手才能达到和人类相似的步行运动。
[1]Sockol M D,Raichlen D A,Pontzer H.Chimpanzee locomotor energetics and the origin of human bipedalism[J].Proceedings of the National Academy of Sciences,2007,104(30):12265-12269.
[2]Hobbelen D G E,Wisse M.Limit Cycle Walking Humanoid Robots,Human-like Machines[M].Vienna:Austria:1-Tech Education and Publisling,2007:14.
[3]卢璥.仿人机器人的发展现状及展望[J].科技信息,2012(21):42,45.LU Jin.Current situation and development prospect of humanoil robots[J].Science and Technology Information,2012(21):42,45.(in Chinese)
[4]梶田秀司,管贻生.仿人机器人[M].北京:清华大学出版社,2007.
[5]陈垦,付成龙.仿人机器人理论与技术[M].北京:清华大学出版社,2010.
[6]Vukobratovic M,Juricic D.Contribution to the synthesis of biped gait[J].Biomedical Engineering,IEEE Transactions on,1969,16(1):1-6.
[7]夏泽洋,陈垦,刘莉,等.面向仿人机器人自然步态规划的人体步行实验分析[J].机器人,2008,30(1):41-46.XIA Ze-yang,CHEN Ken,LIU Li,et al.Experimental analysis on human locomotion for natural gait planning of humanoil robots[J].Robot,2008,30(1):41-46.(in Chinese)
