足球机器人视觉目标识别的PCA-SIFT算法
2013-08-16李彤斐杨马英
李彤斐, 杨马英
(浙江工业大学信息工程学院,浙江杭州310023)
Robocup即机器人世界杯足球锦标赛,是目前国际上最具影响的世界杯机器人足球赛[1]。为了能让一个机器人球队像人类一样进行足球比赛,包含了很多领域技术的融合,比如机械电子学、机器人学、传感器信息融合、智能控制、通信、计算机视觉、计算机图形学、人工智能等。
计算机视觉相当于足球机器人的眼睛,为了让机器人定位自身和其他目标并实现合作与对抗,图像的特征提取以及目标识别是极为关键的一步。特征提取有基于边缘、角、区域和脊的方法。目前已经成熟的特征提取算法有:(1)Hough变换[2];(2)Harris角点检测[3];(3)SIFT 算法[4];(4)SURF算法[5];(5)Mean Shift算法[6]等。Hough 变换于1962年由Paul Hough提出,对圆和直线比较敏感;Harris角点检测在1988年由Harris等人提出,是基于模板的角点检测算法,具有旋转不变性。SIFT算法由D.G.Lowe 1999年提出,其特征能对旋转、尺度缩放、仿射变换、视角变化、光照变化等图像变化因素保持一定的不变性,而对物体运动、遮挡、噪声等因素也保持较好的可匹配性,从而可以实现差异较大的两幅图像之间的特征匹配,可以说应用范围非常广泛,也比较全面。SURF算法由Herbert Bay和Luc Van Gool等人在2006年提出,是SIFT算法的快速算法[7]。Mean Shift算法中的Mean Shift概念最早是由Fukunaga等人于1975年在一篇关于概率密度梯度函数的估计中提出来的,后由Comaniciu等人发展,在图像平滑和图像分割中Mean Shift都得到了很好的应用[8]。
考虑到球场上待识别的物体不只是球、门柱,为了更好地帮助决策系统作出攻守策略判断,识别比赛双方机器人也是非常关键的环节,同时比赛场地存在光照条件变化、场外物体干扰等,移动目标的视频图像也会出现扭曲、模糊等情形,所以认为SIFT算法的全面性能满足类人机器人足球比赛图像处理和目标识别的要求。但是SIFT算法的实时性比较差,这会直接影响到机器人的决策。因此文中借鉴了Yan Ke和 Rahul Sukthankar提出的PCA-SIFT方法[9]。将主成分分析(PCA)算法用于对SIFT算法描述子进行降维,生成低维的PCA-SIFT描述子,并用最近邻法进行特征点匹配,实现机器人场地目标识别。
1 背景知识
1.1 尺度不变特征变换算法原理
尺度不变特征变换(SIFT)算法的计算过程如下:首先构造一个尺度空间,即图像金字塔,并对其差分计算;然后粗略地检测差分金字塔空间中的极值点;再去除一些边缘响应等干扰,以进行精确定位;最后计算每个极值点的梯度值和梯度方向,形成描述子。具体各步骤的描述如下:
1)构造尺度空间 图像的尺度空间L(x,y,σ),定义为一个变化尺度的高斯函数G(x,y,σ)与原图像I(x,y)的卷积

m,n表示高斯模板的维度。
为了高效地检测极值点,Lowe用高斯差分算子代替拉普拉斯算子进行极值检测:

在实际计算中,使用高斯金字塔每组中相邻上下两层图像相减,得到高斯差分图像(DOG),如图1所示。
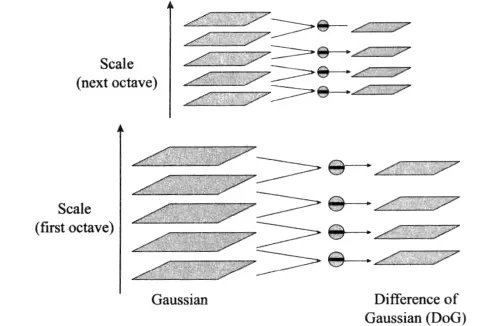
图1 高斯图像金字塔到差分高斯图像金字塔的变换Fig.1 Transformation from Gaussian image pyramid to differential Gaussian image pyramid
2)检测尺度空间极值点 这里指的是初步确定的关键点,即差分高斯金字塔内的局部极值点。如图2所示,共要比较26个相邻点。

图2 DoG空间极值检测Fig.2 Space extremum detection of DoG
3)精确定位极值点 由于DoG值对噪声和边缘较敏感,因此,在上面DoG尺度空间中检测到的局部极值点还要进行进一步的检验才能精确定位。
为了提高关键点的稳定性,需要对DoG空间函数进行拟合:

4)为每个关键点指定方向参数 通过计算每个极值点的梯度值来确定方向。像素点的梯度表示:

梯度幅值:

梯度方向:

完成关键点的梯度计算后,使用直方图统计领域内像素的梯度和方向。梯度直方图将0~360°的方向范围分为36个柱,其中每柱10°。如图3所示,直方图的峰值方向代表了关键点的主方向。

图3 关键点方向Fig.3 Direction histogram of key points
5)关键点描述子生成 首先,确定计算描述子所需的图像区域。其次,将坐标轴旋转为关键点的方向,以确保旋转不变性。再将领域内的采样点分配到8个方向上,计算其权值。插值计算每个种子点8个方向的梯度。如上统计的4×4×8=128个梯度信息即为该关键点的特征向量。
1.2 PCA方法概述
PCA是对数据空间降维进行多元统计分析的方法。它计算主成分的目的是将高维数据投影到较低维空间,一般步骤如图4所示。

图4 PCA方法降维的一般步骤Fig.4 PCA-based dimensionality reduction steps
2 改进的SIFT算法
因为传统的SIFT算法产生的关键点的描述子包含128维的梯度信息,特征匹配时计算量相当庞大,直接影响到算法实时性。文中提出改进的PCA-SIFT目标识别算法,使用PCA方法将128维描述子降维,以提高匹配速度。
改进的SIFT算法主要工作分为3部分,分别如以下各小节描述。
2.1 生成SIFT特征点描述子
改进的SIFT算法中,首先要生成128维的SIFT特征点描述子,这里用的是传统SIFT算法:分别预处理原图像与待匹配的图像,若不为灰度图像就转为灰度图像;然后构造尺度空间,并生成差分图像金字塔;检测尺度空间极值点,为每个极值点确定方向参数;最后生成128维的SIFT特征点描述子。特征向量形成后,为了去除光照变化的影响,需要对它们进行归一化处理。
其中,检测以及精确定位极值点时,为了找到这些点,每一个像素点都要与它的相邻点比较,判断该点是否为极值点。中间的检测点和它同尺度的8个相邻点与上下相邻尺度对应的9×2个点,共26个点比较,以确保在尺度空间和二维图像空间都检测到极值点。为了提高关键点的稳定性,需要对DOG空间函数进行拟合:
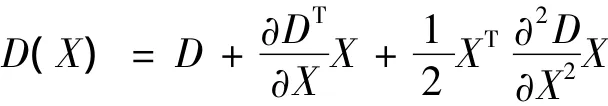
其极值点
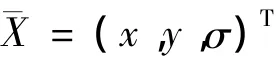
在计算过程中,分别对图像的行、列及尺度进行修正,去除那些对比度较低的不稳定极值点。
对于DoG产生的边缘响应的点,用Hessian矩阵计算主曲率:

DoG的主曲率和H的特征值成正比,为了避免直接计算这些特征值,令特征值为α,β,(α > β)则
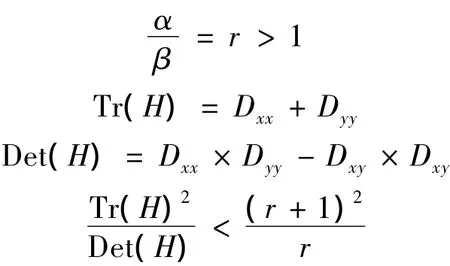
时,将关键点保留,反之剔除。
2.2 PCA对SIFT特征描述子降维
改进的SIFT算法第2步是用PCA方法对SIFT特征描述子进行降维。具体步骤如下:
1)输入两幅待匹配图像中所有关键点(设为n个)的128维SIFT特征描述符,将输入的这n个特征描述符作为样本,写出样本矩阵为[x1,x2,…,xn]T,其中xi表示第i个特征点的128维特征向量。
2)计算n个样本的平均特征向量:
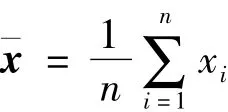
4)构建协方差矩阵
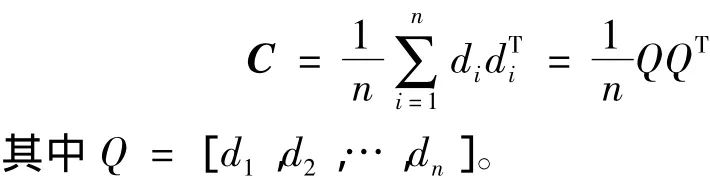
5)求协方差矩阵的128个特征值λi和128个特征向量ei。
6)将求出的128个特征值按从小到大的顺序进行排列λ1≥λ2≥…≥λ128和对应的特征向量[e1,e2,…,e128]。
7)选取对应t个最大特征值的特征向量作为主成分方向。
8)构造一个128×t的矩阵A,它的列由t个特征向量组成。
9)把原始的128维描述符根据下式投影到所计算出的n维子空间M中,就可以得到PCA-SIFT的描述符 y1,y2,…,yn了,即 yi=xi× A。
实验中,矩阵A的大小为128×t,xi的大小为1 ×128,即xi×A的大小为1×t,即每一个yi就是一个t维的特征描述子,也就是把传统的128维SIFT描述子降成了t维的PCA-SIFT描述子。
2.3 特征点匹配
在提取完特征点之后,改进的SIFT算法第3步,即特征点匹配。这里选用最近邻的方法进行匹配。对于待匹配图像中的一个特征点,把它逐一与已知图像中的特征点计算欧氏距离,找出距离最近与次近的点,当最近点与次近点的比值小于一个阈值时,认为这两点是匹配的。计算时运用以下公式:

其中,D1为最近点距离,D2为次近点距离。
3 实验及结果
实验需要在机器人足球比赛场地抓取一些图像(像素为500×836)。如图5所示,左侧全部为原图,右侧分别为扭曲后、光照变暗以及用于识别比赛双方机器人的图像。

图5 待处理的3对图像Fig.5 Three pairs of images to be processed
实验配备的计算机为Mobile AMD Sempron(tm)Processor 3200+ 处理器,内存为1.60 GHz,960 MB。仿真平台为 Matlab7.0.1。
针对上述存在图像扭曲、光照变化以及双方机器人的图像,分别运用SIFT算法与PCA-SIFT算法提取特征点,并用最近邻法进行匹配,观察算法的计算效率与匹配结果。计算中PCA-SIFT的参数t取10,匹配算法的参数 r取0.6。
图6 为图像扭曲后与原图的匹配效果。可以发现(b)图明显比(a)图的匹配对数少,即经过改进的PCA-SIFT算法有明显的降维作用,但是(b)图正确匹配率不如(a)图高,说明改进的PCA-SIFT算法在图像扭曲的情况下效果不是很好。
图7 为双方机器人的识别效果。图中机器人分别与原图的我方机器人进行匹配(用线条连接两幅图像中认为匹配的点)。匹配度高的一方为我方机器人,反之为对方机器人。可以发现,图7(a),(c)显然比图7(b),(d)的匹配对数多,此时认为图像中左侧机器人为我方机器人,右侧机器人为对方机器人。

从表1统计的数据可以发现,PCA-SIFT算法在图像扭曲与双方机器人识别方面于SIFT算法相比较,匹配对数明显下降,有很显著的降维作用;而在光照变化的条件下降维不太明显。另外,在双方机器人识别方面,图7b,d比图7a,c的匹配对数少很多,可以判断图7b,d为对方机器人。
从表2统计的数据中可以发现,在3种条件下PCA-SIFT都能保持较好的匹配率,特别是在光照变化和双方机器人识别方面占有优势。另外,用匹配率的数据同样可以判断是否为我方机器人,本实验数据显示对方机器人的匹配率为零,则匹配率不为零的为我方机器人。
受限于计数器的精度,文中采集的图像均为500×836 像素,而在Robocup比赛中机器人抓图得到的图像像素较低,所以相对而言统计出来的匹配时间较长。从表3可以发现,PCA-SIFT算法普遍比SIFT算法快,特别是在光照变化的条件下省下的时间比较多。

表1 不同条件下2种算法的匹配对数Tab.1 Number of matching pairs单位:对

表2 正确匹配率Tab.2 Correct matching rate单位:对 /对
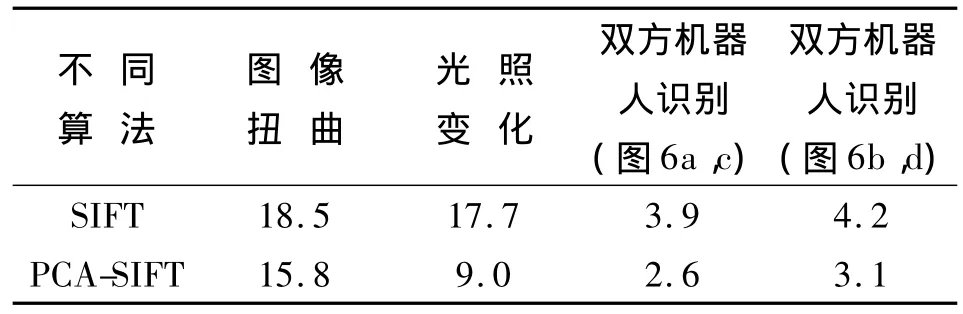
表3 不同条件下2种算法的匹配时间Tab.3 Matching time under different conditions单位:s
综合以上结果,可以得出结论:SIFT算法用于机器人足球的场景来识别比较复杂的目标时有很好的识别率;经过改进的SIFT算法,即PCA-SIFT算法较SIFT算法有降维加速计算的效果,同时能保持较高的匹配率,且在识别双方机器人方面有较强的优势。
4 结语
文中提出改进的PCA-SIFT目标识别算法,将经典SIFT算法与PCA方法相结合,获取低维的PCA-SIFT描述子,之后用最近邻方法完成特征点匹配。该方法与传统SIFT算法在多种场景条件下作了对比,实验证明在机器人足球比赛场景下经过改进的PCA-SIFT目标识别算法既保持了匹配率,又缩短了匹配时间,是一种机器人足球比赛适用的提取方法。
[1]Vadakkepat P,Sin N B,Goswami D.Soccer playing humanoid robots:processing architecture,gait generation and vision system[J].Robotics and Autonomous Systems,2009,57:776-785.
[2]梁霄颖,李永新,张杰,等.Hough变换在足球机器人视觉处理中的应用[J].机械设计与制造,2008(1):167-169.LIANG Xiao-ying,LI Yong-xin,ZHANG Jie,et al.Applications of Hough transform in soccer robot vision processing[J].Mechanical Design and Manufacture,2008(1):167-169.(in Chinese)
[3]Harris C,Stephens M.A combined corner and edge detector[C]//Manchester:Proceedings of the 4th Alvey Vision Conference.Manchester,UK:The University of Sheffield Printing Unit,1988:147-151.
[4]Lowe D G.Distinctive image features from scale-invariant key-points[J].International Journal of Computer Vision,2004,17(1):43-76.
[5]Bay H,Gool V.SURF:speeded up robust features[C]//European Conference on Computer Vision.Graz,Austria:Springer-Verlag,2006,1:404-417.
[6]Comaniciu D,Meer P.Mean shift:a robot approach toward feature space analysis[J].IEEE Transaction on Panttern Analysis and Machine Intelligence,2002(5):603-619.
[7]Khan N Y,McCane B,Wyvill G.SIFT and SURF performance evaluation against various image deformations on benchmark dataset[C]//International Conference on Digital Image Computing:Techniques and Applications.Queensland,Australia:IEEE Computer Society,2011,9:501-506.
[8]ZHOU H Y,YUAN Y,SHI C.Obiect tracking using SIFT features and mean shift[J].Computer Vision and Image Understanding,2009,113:345-352.
[9]Ke Y,Sukthankar R.PCA-SIFT:a more distinctive representation for local image descriptors[C]//Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Washington DC:IEEE Computer Society,2004.
